
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Стабильные и эффективные оптимальные решения на основе коалиционного равновесияСтр 1 из 5Следующая ⇒ 3.1. Классификация стабильных и эффективных решений Понятие коалиционного равновесия базируется на фундаментальном понятии V-решения, сформулированном в работе [39] (см. реферат данной работы в приложении работы1) при достаточно общем определении игры. Определение 3.1 [39]. Игрой называется набор Г = {N, S, {XK}, S(xK), { где N – произвольное множество объектов, S – произвольное множество исходов игры, где в частном случае исход – значение показателя, XK – произвольное множество стратегий-решений коалиции KÌN, S(xK)ÌS – множество возможных исходов, если коалиция K применяет стратегию-решение xKÎXK, Определение 3.2 [39]. Пара (K, xK), xKÎXK¹Æ называется угрозой против исхода sÎS, если Определение 3.3 [39]. Пара (Q, xQ), xQÎXQ ¹ Æ называется контругрозой на угрозу (K, xK), если KÇQ¹ Æ и для некоторого Поясним определения 3.2 и 3.3. Пусть S = J(X) – множество достижимости значений функционалов – показателей эффективности игры на множестве решений X, где x = (x1,…,xN)ÎX, s = J(x)ÎS. Отношение предпочтений В свою очередь, решение xQ коалиции Q является контругрозой относительно угрозы xK коалиции K, если KÇQ¹Æ, и для некоторого  Определение 3.4 [39]. Угроза считается эффективной, если на нее нет контругрозы. Исход игры считается оптимальным, если против него нет эффективных угроз. Множество всех оптимальных исходов есть В [39] утверждается, что «в настоящее время кроме V-решения нет другого столь же простого, удобного для уточнений, но более сильного универсального решения». Существование V-решения связано с отсутствием «запрещенных ситуаций» в игре. Определение 3.5 [39]. Игра называется игрой без запрещенных ситуаций, если для любой ее реализации (P,x(P)) где P – коалиционное разбиение, x(P) = (xK)KÎP – набор решений (ситуация). Отсутствие запрещенных ситуаций означает, что игру можно разыграть без согласования действий непересекающихся коалиций, когда независимый выбор любой коалицией своих решений в рамках данной структуры P приводит к исходу игры. Классы бескоалиционных и коалиционных игр, это, в основном, игры без запрещенных ситуаций. При ограничении действия коалиции выбором компонент дележа лишь своих членов кооперативная игра также является игрой без запрещенных ситуаций. Утверждение 3.1 [39]. Для любой игры без запрещенных ситуаций существует такая реализация игры (P, x(P)), что Э. Вилкас [39] отмечает, что в общем случае V-решение носит характер предрешения, когда понятие оптимальности может уточняться и дополнить предрешение. При этом под уточнением решения автор понимает определение решения более узкого, чем V-решение, путем наложения дополнительных условий на контругрозу и модификации угрозы. Ограничимся в дальнейшем более узким классом коалиционных игр Г = {N, (XK), (JK)}, KÎРÌР, (3.4) где N – множество объектов; Для произвольной коалиционной структуры P, xP = {xK}KÎP, xK ÎXK. Тогда уточнение понятия V-решения может быть сформировано в виде коалиционного равновесия. Определение 3.6 [39]. Ситуация либо либо Таким образом, ситуация Очевидно, что принадлежность Поэтому коалиционное равновесие определяется тремя «динамическими» факторами: множеством коалиционных структур P, видом Утверждение 3.2. В общем случае коалиционное равновесие реализуется на допустимом множестве коалиционных структур P (PÎP), которое определяется «начальным» P, набором возможных угроз KÏP и набором соответствующих контругроз (N\K)ÏP. Наиболее общим коалиционным равновесием является сильное равновесие. Определение 3.7 [39]. Коалиционное равновесие называется сильным (абсолютным) равновесием Против сильного равновесия, очевидно, нет угроз. Кроме того, оно является равновесием при любом P. Поэтому сильное равновесие является коалиционным равновесием при любом P. Определение 3.8. Множество собственно коалиционных равновесий определяется множеством оптимальных исходов в V-решении (множеством неэффективных угроз) на допустимом множестве коалиционных структур P при локальной Парето оптимизации в рамках коалиции. К собственно коалиционным равновесиям относится понятие угроз и контругроз (УКУ-решения), введенное Вайсбордом–Жуковским [32, 50] (см. также гл. 4). Определение 3.9. При отсутствии угроз (частный случай V-решения) и фиксации коалиционной структуры P коалиционное равновесие Определение 3.10. При отсутствии угрозы и фиксации коалиционной структуры в виде одной коалиции K = N коалиционное равновесие «Сужение» множества решений может быть обеспечено тем или иным подходом Парето-оптимизации, например, W-оптимизацией на основе конусов доминирования [47, 428, 430] W = (x: BJ(x) ³ 0), (3.5) где B – матрица конуса доминирования W. Этот подход Парето-оптимизации принят как основной в данной главе. Определение 3.11. Подмножество не равны единичной матрице BK ¹ E хотя бы частично. Определение 3.12. При отсутствии угроз, фиксации коалиционной структуры P и полной свертке показателей коалиции коалиционное равновесие Определение 3.13. При отсутствии угроз, фиксации набора коалиционных структур P (PÎP) и свертке показателей коалиции коалиционное равновесие принимает вид кооперативного решения Харшаньи–Скеруса на основе множества недоминируемых Нэш-равновесий на P [32]. Данная классификация не претендует на полноту и может быть продолжена. Но даже и в представленном виде она показывает, что понятие коалиционного равновесия является достаточно универсальным и включает, как частные случаи, поиск эффективных решений (Парето-оптимальных, W-оптимальных и т.д.) и стабильных решений (скалярных Нэш-решений, векторных Нэш-решений, W-равновесных и т.д.). |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 873. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 }}, (3.1)
}}, (3.1)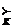 – транзитивное отношение предпочтений коалиции
– транзитивное отношение предпочтений коалиции 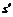
 ÎS(xQ) имеет место
ÎS(xQ) имеет место 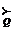
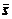
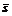 принимает вид
принимает вид  , где JK – показатель коалиции KÌN. Подмножество S(xK)ÌS состоит из величин J(x||xK) при фиксированном решении xKÎXK коалиции K. Решение xK коалиции K является угрозой относительно исхода игры s = J(x), если для любого
, где JK – показатель коалиции KÌN. Подмножество S(xK)ÌS состоит из величин J(x||xK) при фиксированном решении xKÎXK коалиции K. Решение xK коалиции K является угрозой относительно исхода игры s = J(x), если для любого  ||xK)ÎS(xK) имеет место JK(
||xK)ÎS(xK) имеет место JK(  ||xQ)ÎS(xQ), JQ(
||xQ)ÎS(xQ), JQ( 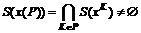 , (3.2)
, (3.2)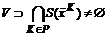 . (3.3)
. (3.3) – множество стратегий-решений коалиции KÌN; JK = {Ji(x)}iÎK – векторная функция эффективности коалиции K, xÎXN (исходы игры Г).
– множество стратегий-решений коалиции KÌN; JK = {Ji(x)}iÎK – векторная функция эффективности коалиции K, xÎXN (исходы игры Г).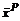 называется коалиционным равновесием, если принадлежит V-решению и для любых KÎPÌP и xKÎXK:
называется коалиционным равновесием, если принадлежит V-решению и для любых KÎPÌP и xKÎXK: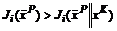 хотя бы для одного iÎK,
хотя бы для одного iÎK,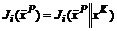 для всех iÎK.
для всех iÎK.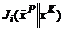 в XK в том смысле, что если другая стратегия-решение дает больший выигрыш игроку iÎK , то одновременно она дает меньший выигрыш игроку jÎK .
в XK в том смысле, что если другая стратегия-решение дает больший выигрыш игроку iÎK , то одновременно она дает меньший выигрыш игроку jÎK .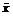 , если оно оптимально по Парето в
, если оно оптимально по Парето в 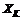 относительно
относительно 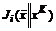 , (iÎK) для всех K Ì N.
, (iÎK) для всех K Ì N.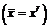 , так как устойчивость данного равновесия определяется потерей эффективности при отклонении K-й коалиции от Парето-решения
, так как устойчивость данного равновесия определяется потерей эффективности при отклонении K-й коалиции от Парето-решения 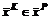 относительно вектора
относительно вектора  , iÎK.
, iÎK.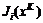 ,
, 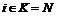
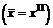 .
.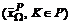 ВНР-решений называется W-равновесием
ВНР-решений называется W-равновесием 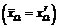 , если матрицы BK, KÎP многогранных конусов доминирования Парето-оптимизации коалиции K
, если матрицы BK, KÎP многогранных конусов доминирования Парето-оптимизации коалиции K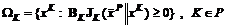
 (3.6)
(3.6)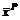 приобретает смысл скалярного Нэш-равновесия.
приобретает смысл скалярного Нэш-равновесия.