
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задачи для самостоятельного решенияДля изготовления четырех видов продукции используются три вида сырья. Исходные данные представлены в таблице 3.3. (Примечание: в исходной таблице заменяется столбец «запасы» или строка «прибыль» в соответствии с номером варианта).
Таблица 3.3
Необходимо: 1.Записать прямую задачу. Определить план выпуска продукции, при котором прибыль от ее реализации будет максимальной (при решении задачи показать все промежуточные симплекс-таблицы – просто решить в EXCEL без промежуточных вычислений не допускается – в этом случае задача защитываться не будет. Допускается использование EXCEL для проверки правильности решения). В остальных пунктах использовать таблицы EXCEL для ответа на вопросы допускается – но при этом необходимо их интерпретировать, т.е. пояснить смысл полученных значений. 2. Записать двойственную задачу. Получить решение двойственной задачи. Пояснить экономический смысл полученных объективно обусловленных (теневых) оценок ресурсов. 3.Найти интервалы устойчивости двойственных оценок по отношению к изменению запаса ресурсов каждого вида. 4.Определить изменение максимальной прибыли от реализации продукции при увеличении запаса ресурса 1 на 10 ед., ресурса П – на 50 ед. и уменьшении запаса ресурса Ш на 30 ед. Оценить раздельное влияние этих изменений и суммарное влияние. 5.Сопоставить оценку затрат и прибыли по оптимальному плану и каждому виду продукции. 
Примечание: в исходной таблице заменяется столбец «запасы» или строка «прибыль» в соответствии с номером варианта
Вариант1 Вариант2 Вариант3 Вариант4 Вариант5 Вариант6
Вариант7 Вариант8 Вариант9 Вариант10 Вариант11 Вариант12
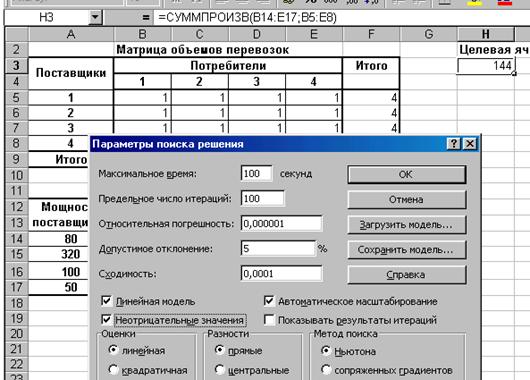
Контрольное задание №4. Транспортная задача или Модели управления запасами Методические указания Транспортная задача является специальным типом задач линейного программирования. Экономическая постановка этой задачи следующая: имеется m поставщиков и n потребителей некоторой продукции. Заданы тарифы (стоимость) перевозок единицы продукции от поставщиков к потребителям, известны объемы запасов у поставщиков и потребности каждого потребителя в продукции. Требуется составить план поставок продукции от поставщиков к потребителям так, чтобы суммарная стоимость перевозок была минимальной. Математическая постановка этой задачи имеет вид Здесь Xij – объем; cij – тариф поставки продукции от i-го поставщика к j-му потребителю; bj – потребности потребителей в продукции; ai - запасы продукции у поставщиков. Исходные данные транспортной задачи оформляются в виде табл.4.1, где заданы мощности поставщиков и потребности потребителей, а также транспортные затраты на перевозку единицы продукции от поставщиков к потребителям. Таблица 4.1 Исходные данные транспортной задачи
При решении транспортной задачи в системе Excel исходные данные записываются в две таблицы и формируется вычисляемая ячейка значения целевой функции. В изменяемую таблицу Объемы перевозок первоначально для контроля вводятся единицы. В таблицу исходных данных задачи вводятся данные табл. 4.1.
Рис. 4.1. Таблицы Excel для решения транспортной задачи
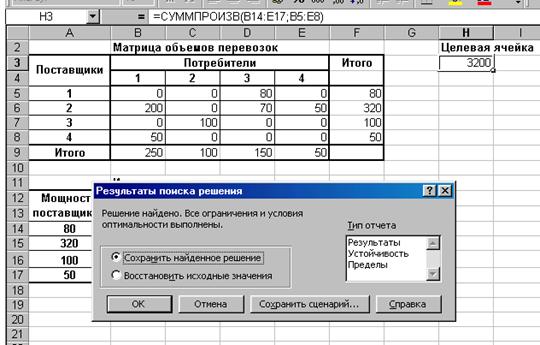
В целевую ячейку записана функция СУМПРОИЗ(В14:Е17;В5:Е8), которая вычисляет совокупные затраты на перевозку грузов от поставщиков к потребителям. В ячейках Итогопомещены формулы сумм объемов перевозок по строкам и столбцам, затем вызывается функция Поиск решенияи осуществляется ввод данных в окно функции (рис. 4.2).
Рис. 4.2. Ввод данных в окно функции Поиск решения при решении транспортной задачи.
Затем вводятся ограничения по мощностям поставщиков и потребителей.
Рис. 4.3. Ввод ограничений транспортной задачи
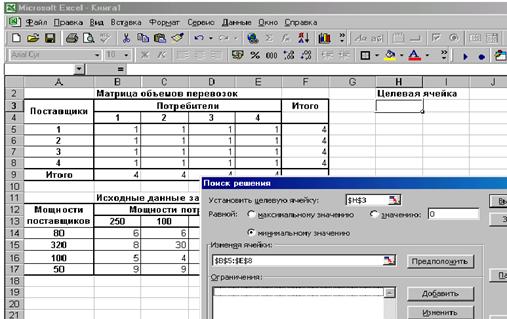
В окне Параметры поиска решения устанавливаются параметры решения задачи (рис. 4.4). После этого выполняется возврат в окно Поиск решения, где нажимается кнопка Выполнить(см. рис. 4.5). Анализ содержания таблицы позволяет сделать вывод, что минимальные затраты на перевозку всех грузов равны 3200 ед.. Объемы перевозок отражены в таблице Матрица объемов перевозокна том же рисунке. Таким образом, решение найдено.
Рис. 4.4. Ввод параметров решения транспортной задачи
Рис. 4.5. Решение транспортной задачи
Модели управления запасами Основная цель управления запасами — достичь приемлемого уровня обслуживания потребителей, удерживая расходы на поддержание запасов в разумных пределах. Два основных вопроса, которые при этом приходится решать, — это сроки и объемы заказов, то есть когда и сколько заказывать. Выбирается промежуток времени. Рассматривается модель одиночного склада. Считается, что на складе хранится запас однотипных изделий (однономенклатурный запас). Спрос на эти изделия может быть постоянным или случайным. Пополняться склад может либо периодически (циклическая модель), либо при снижении запасов до некоторого уровня (уровневая модель). Объем заказа — это количество заказываемых изделий. Уровень повторного заказа — количество изделий на складе, при котором подается заказ на новые изделия. Время поставки может быть либо мгновенным, либо случайным. Штраф за дефицит — это убытки, связанные с отсутствием запаса. Такие издержки возникают, когда спрос превышает наличные запасы, и включают возможные потери от нереализованных продаж, потерю доверия клиентов и т. д. За хранение каждой единицы запаса берется определенная плата. Стоимость хранения — это расходы, связанные с содержанием товара на складе в течение определенного времени. Сюда относятся собственно складские расходы (арендная плата, охрана, отопление, освещение и т. д.), страховка, издержки от старения, износа, порчи, мелких хищений, проценты и т. д. Стоимость хранения включает также и издержки, связанные с вложением в материальные запасы денежных средств, которые можно было бы прибыльно использовать где-то еще. Стоимость подачи заказа — это накладные расходы, связанные с реализацией заказа (затраты на подготовительно-заготовочные операции, не зависят от объема заказа). Сюда входят определение нужного объема заказа, оформление счетов-фактур, проверка партии поставки на количество и качество, перемещение запасов на хранение. Вся теория строится с целью минимизации издержек. Предпосылки основной модели: 1) спрос равномерный и постоянный; 2) время поставки постоянно; 3) отсутствие запасов недопустимо; 4) каждый раз заказывается постоянное количество — оптимальный размер заказа. Рассмотрим модель без дефицита Суммарные издержки
где θ – время, в течение которого расходуется продукт N – общее потребление b – интенсивность расхода
Количество партий Время расхода партии Решением этой оптимизационной задачи, т.е. минимизации суммарных издержек, будет значение наиболее экономичного объема партии
Минимальные затраты Число оптимальных партий
Время расхода оптимальной партии
В модели с дефицитом в функцию суммарных затрат также добавляются затраты на штраф из-за дефицита
Где
s – размер запаса n – объем партии. Решением этой оптимизационной задачи будет значение наиболее экономичного объема партии
и максимального уровня запаса
Суммарные затраты рассчитываются путем подстановки оптимальных значений
Пример. Годовой спрос 1500 единиц, стоимость подачи заказа 150 рублей/заказ, издержки хранения одной единицы 45 рублей/год, время доставки 6 дней, 1 год = 300 рабочих дней. Найти оптимальный размер заказа, издержки, уровень повторного заказа.
Порядок выполнения задания: Оптимальный размер заказа Минимальные издержки Число оптимальных партий За 300 рабочих дней реализуется 1500 единиц, за 6 дней доставки - x единиц. Расстояние между циклами
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 326. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
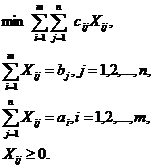 (4.1)
(4.1)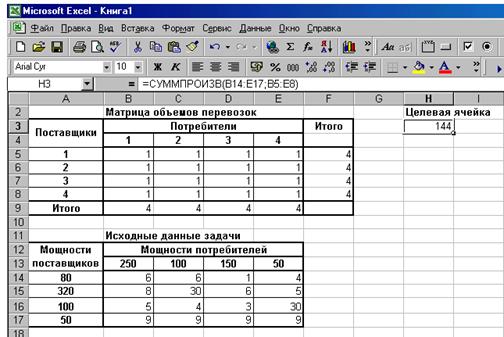

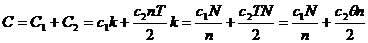 (4.2)
(4.2)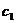 - затраты на доставку одной партии продукта
- затраты на доставку одной партии продукта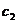 - затраты на хранении одной единицы продукта в единицу времени.
- затраты на хранении одной единицы продукта в единицу времени.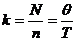 (4.3)
(4.3) (4.4)
(4.4)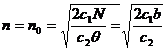 (4.5)
(4.5) (4.6)
(4.6)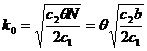 (4.7)
(4.7)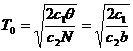 (4.8)
(4.8)
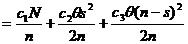 (4.9)
(4.9)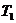 - время, в течение которого производится потребление запаса
- время, в течение которого производится потребление запаса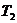 - время, в течение которого накапливается дефицит
- время, в течение которого накапливается дефицит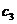 - штраф за дефицит в единицу времени на каждую единицу продукта
- штраф за дефицит в единицу времени на каждую единицу продукта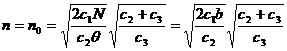 (4.10)
(4.10)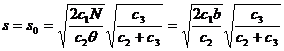 (4.11)
(4.11)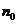 и
и 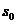 в формулу 4.9, число оптимальных партий - путем подстановки оптимального
в формулу 4.9, число оптимальных партий - путем подстановки оптимального 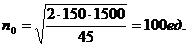
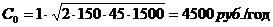
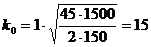
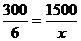 . Отсюда x = 30 единиц. Каждый раз, когда на складе остается 30 единиц, подается заказ на 100 единиц.
. Отсюда x = 30 единиц. Каждый раз, когда на складе остается 30 единиц, подается заказ на 100 единиц.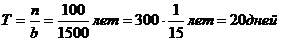 .
.