Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оптимизация проекта по времени.Сокращение времени завершения проекта, как правило, связано с привлечением дополнительных средств (количество рабочих, сверхурочные работы). Рассмотрим два примера задачи оптимизации проекта по времени с привлечением дополнительных средств.
Постановка задачи 1. Для сокращения времени выполнения проекта выделяется некоторая сумма дополнительных средств В. Задан сетевой график выполнения проекта, продолжительность каждой работы равна tij. Известно, что вложение дополнительных средств хij в работу (i,j) сокращает время ее выполнения от t до t'ij, причем эта зависимость выражается как t'ij = fij(xij) £ tij (fij — известные функции). Для каждой работы существует минимально возможное время ее выполнения dij. Если предположить, что продолжительность выполнения работ линейно зависит от дополнительно вложенных средств и выражается соотношением t'ij = tij - kij xij , где kij — технологические коэффициенты использования дополнительных средств, то будем иметь задачу линейного программирования. Требуется определить время начала tHij и окончания t°ij выполнения работ, а также количество дополнительных средств хij, которые необходимо вложить в работы (i,j), чтобы общее время выполнения проекта было минимальным, сумма вложенных дополнительных средств не превышала величины В, время выполнения каждой работы было не меньше минимально возможного времени. Математически условия задачи можно записать следующим образом: tкр = to n-1,n (min) (2.15)
t°ij - tHij³ dij , (2.17)  t°ij - tHij = fij , (2.18) tHrj ³ t°ir , (2.19) t°ij ³ 0, tHij ³ 0. (2.20)
Выражение (2.15) – целевая функция. Ограничение (2.16) определяет сумму вложенных дополнительных средств: она не должна превышать величины В. Ограничения (2.17) показывают, что продолжительность каждой работы должна быть не менее минимально возможной ее продолжительности. Ограничения-равенства (2.18) показывают зависимость продолжительности каждой работы от вложенных в нее дополнительных средств. Ограничения (2.19) обеспечивают выполнение условий предшествования работ в соответствии с топологией сети: время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующих ей работ. Ограничение (2.20) — условие неотрицательности. Если в последнее событие сети n входят сразу несколько работ, то необходимо добавить фиктивную работу (n,n+1), время выполнения которой равно нулю и добавить ограничение (t°n,n+1 - tHn,n+1 = 0) в (2.17).
Постановка задачи 2. Пусть задан срок выполнения проекта tо, а расчетное время tкр³to. В этом случае оптимизация комплекса работ сводится к сокращению продолжительности критического пути. Задача заключается в определении величины дополнительных вложений xij в отдельные работы проекта с тем, чтобы общий срок его выполнения не превышал заданной величины to, а суммарный расход дополнительных средств был минимальным. Время выполнения каждой работы должно быть не меньше минимально возможного времени dij. Математическая запись этой задачи: F(x)= to n-1,n £ to, t°ij - tHij³ dij , t°ij - tHij = fij , tHrj ³ t°ir , t°ij ³ 0, tHij ³ 0.
Смысл ограничений аналогичен соответствующим ограничениям постановки задачи 1. В каждом варианте в сетевой график добавляется еще одна работа. При оптимизации графика рекомендуется построить таблицу вида
В таблице заполняются столбцы 1-4. В столбцы 8-9 записываются формулы. В каждом варианте в ячейке в конце столбца xij рассчитывается сумма xij. Задача решается при помощи функцииСервис -«Поиск решения». В поле «Установить целевую ячейку» команды «Поиск решения» выделите ячейку со значением целевой функции модели (это будет или ячейка с суммой xij или ячейка t0(n-1,n), т.е. время окончания последней работы). Чтобы минимизироватьзначение целевой ячейки, установите соответствующее положение переключателя.
В поле «Изменяя ячейки» введите адреса переменных модели, выделяя блок этих ячеек (во всех вариантах это будут столбцы tн(ij), t0(ij), xij). Щелкните по полю Ограничения, после чего введите ограничения, накладываемые на решение задачи. Для этого нажмите кнопку Добавить. В поле Ссылка на ячейку выберите ячейку или диапазон ячеек, на значения которых накладываются ограничения. Во всех вариантах ограничения tоij - tнij³ dij , tоij - tнij = tij-kij*xij, tнrj ³ tоir будут одинаковы, только в одних вариантах добавится ограничение to n-1,n £ to, где to берется по варианту (ограничение на время), а в других - это будет ограничение Чтобы ввести ограничение и приступить к набору нового, нажмите кнопку Добавить, а чтобы вернуться в диалоговое окно Поиск решения, нажмите кнопку OK. В окне Параметры поиска решения для решения линейных задач надо установить флажки Линейная модель и Неотрицательные значения.
Нажмем кнопку OK и вернемся в окно команды Поиск решения. Затем нажмем кнопку Выполнить, и, если все сделано правильно, то в таблице данных получим результаты решения задачи. Пример.
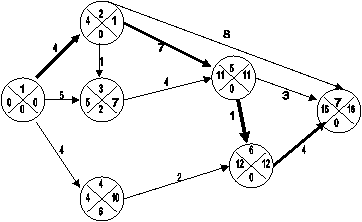
Дан сетевой график, найти все характеристики событий и работ.
Рис.2.1.Сетевой график схарактеристиками событий
1.Рассчитаем характеристики событий.Для наглядности каждое событие сетевого графика разделено на 4 сектора. Верхний сектор соответствует номеру события, в левом секторе записан ранний срок tp(i) наступления события i, в правом – поздний срок tп(i) наступления события i, в нижнем секторе представлен резерв времени R(i) события i. Эти же характеристики представлены в таблице, приведенной ниже.
Анализ таблицы и сетевого графика показывает, что критический путь имеет вид (1-2-5-6-7), а его длина равна tкр=16. 2. Перейдем к определению характеристик работ. Отдельная работа может начаться и окончиться в ранние, поздние или другие промежуточные сроки. В дальнейшем при оптимизации сетевого графика возможно любое размещение работ в заданном интервале. Все расчеты сведены в табл.3.2.(столбцы 2-9)
Таблица 3.2.
Анализ таблицы и сетевого графика показывает, что критический путь имеет вид (1-2-5-6-7), а его длина равна tкр=16. 3. После нахождения критического пути (1-2-5-6-7) длины 16 перейдем к определению коэффициентов напряженности работ. Рассмотрим работу (3,5) и найдем все полные пути, проходящие через эту работу, и соответствующие им длины:
L1: 1-2-3-5-7; t(L1)=12 ; L2: 1-3-5-7; t(L2)=12 ; L3: 1-3-5-6-7; t(L3)=14 ; L4: 1-2-3-5-6-7; t(L4)=14 .
Через работу (3,5) проходит два максимальных пути длины 14. Выберем второй из них. Тогда t'кр=9 - длина части (1-2, 5-6-7) пути (1-2- 3-5-6-7), совпадающей с критическим путем (1-2-5-6-7). Воспользуемся формулой расчета коэффициента напряженности, в результате получим, что
Rн(3,5) = 1-Rп(3,5) / (tкр-t'кр)=1-2/(16-9)=0,7.
Для остальных работ коэффициент напряженности находится аналогичным способом.
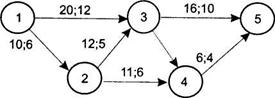
Пример.Оптимизация сетевого графика. Для сокращения срока реализации проекта, представленного сетевым графиком (рис.2.2), заказчик выделил 14 ед. дополнительных средств. Продолжительность выполнения работ линейно зависит от дополнительно вложенных средств и выражается соотношением t'ij = tij - kij xij . Известно, что k12 = 0,1; k13 = 0,2; k23 = 0,5; k24 = 0,3; k35 = 0,6; k45 = 0,1. Над каждой работой поставлены ее продолжительность tij и минимально возможное время выполнения dij .
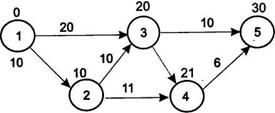
Рис. 2.2 Требуется оптимизировать сетевой график по времени, то есть найти такие tн ij, t° ij , x ij, чтобы: а)время выполнения всего проекта было минимальным; б)сумма дополнительно вложенных средств не превышала 14 ед.; в)продолжительность выполнения каждой работы была не меньше заданной величины dtj. Добавим на сетевом графике фиктивную работу (5, 6), как показано на рис. 2.3.
Рис. 2.3
Тогда целевая функция запишется в виде tкр = t° 5,6 ( min) Запишем ограничения задачи: а) сумма вложенных средств не должна превышать их наличного количества х12 + х13 +х45 + х 23+ х2 4+ х35 £ 14; б) продолжительность выполнения каждой работы должна быть не меньше минимально возможного времени: t012-tн12³ 6; t013-tн13 ³ 12; t023-tн23³ 5; t024-tн24³ 6; t034-tн34 = 0; t035 - tн35 ³ 10; t045 - tн45³ 4; t056-tн56 =0; в)зависимость продолжительности работ от вложенных средств t012-tн12 =10-0,1 х12 ; t013-tн13 = 20-0,2 х13; t024-tн24 = 11- 0,3 х2 4; t035 - tн35 = 16-0,6 х35 ; t045-tн45= 6 – 0,1 х45 ; t023-tн23 =12 – 0,5 х 23. г) время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующей ей работы tн12 = 0; tн13 = 0; tн23³ t012; tн34³ t013 ; tн34³ t023 ;tн24³ t012; tн35 ³ t013; tн35 ³ t023 ; tн45 ³ t024; tн56 ³ t035 ; tн56 ³ t045; tн45 ³ t034 . д) условие неотрицательности неизвестных tHij³ 0; t°ij ³ 0; t°ij ³ 0, (i, j)Î U. Решив данную задачу симплекс-методом на ПЭВМ, получаем: tн12 = 0; t°12 = 10; tн13 = 0; t013= 20; tн23 = 10; t023= 20; tн24= 10; t°24 = 21; tн34 = 20; t034= 20; tн35 = 20; t°35 = 30; tн45= 24; t°45 = 30; tH56 = 30; t056 = 30;x12 = 0; x13 = 0; x23 = 4; x24 = 0; x35 = 10; x45 = 0;tKP = 30. Таким образом, при дополнительном вложении 14 ед. комплекс работ может быть выполнен за 30 ед. времени. При этом средства распределятся следующим образом: 4 ед. в работу (2, 3) и 10 ед. в работу (3, 5) (рис.2.4).
Рис. 2.4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 658. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 £ B; (2.16)
£ B; (2.16)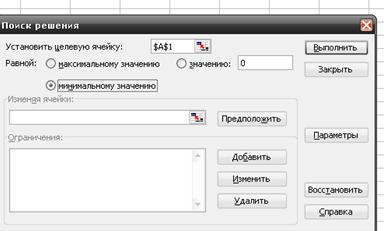
 £ B, где В берется по варианту (ограничение на затраты).
£ B, где В берется по варианту (ограничение на затраты).