
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Фотон . Фотон импульсы энергиясы . Комптон эффектісі. ⇐ ПредыдущаяСтр 6 из 6 Фотон – электромагниттік сәуленің кванты. Жарық сәулесінің энергиясының шығарылып, сонымен қатар кеңестікте таралуы және заттармен әсерлесуі фотондар бөлшегі арқылы сипатталады. Фотон энергиясы Е=ҺV Фотон импульсы P=mc=ҺV/c Векторлық түрде P=𝒽k импульс бағыты электромагнит сәулесінің таралу бағытымен сәйкес келеді. K – толқындық сан. Фотонның тыныштық массасы m0=0. Тең болғандықтан , тек қозғалыста өмір сүре алады. Бар болғаны бір бөлшектен тұрады. Комптон эффектісі – рентген сәулесі шашыраған кезде олардың толқын ұзындығының өзгеруі жарықтың корпускалық қасипетінің айқын дәлелі комптон эффектісі болып табылады.
64. Жартылай өткізгіштер. ЖӨ меншікті өткізгіштігі. Фотокедергі. Жартылай өткізгіштер изолятормен өткізгіштер арасында жатады. Алайда оған тән қасиет өткізгіштің температураға байланысты байланыстылығы, температура өскенде тез өседі, ал металды алсақ кемиді. ЖӨ меншікті ж/е қоспа болып екіге бөлінеді. Меншікті ЖӨ қатарына химиялық таза жартылай өткізгіштер жатады. Ал қоспасында табиғи түрде басқа атомдарды еңгізеді. ЖӨ-ң электрлік қасиетін қарастырғанда “кемтік” деген түсініктің маңызы зор. Температурасы жоғарылаған жағдайда, валенттік зонадағы электрондар өткізгіштік зонаға өтеді, бос қалған орынға басқа эл-р ие болады. Бұл валенттік зонадағы эл-дардың қозғалысын оң таңбалы заряды бар квазибөлшек ретінде қарастырып, бөлшекті “кемтік” деп атайды.  ЖӨ-ң меншікті өткізгіштігі. Меншікті өткізгіштік эл-дардың жоғары валенттік зонадағы деңгейден өткізгіш зонасына өтуімен сипатталады. Валенттік зонадағы бос қалған орынды кемтіктер өткізгіштігі деп атайды. Сондықтан меншікті өткізгіште (электроды мен кемтіктер) тоқ тасымалдайтын бөлшектер электрондар мен кемтіктер. 65. Жылулық сәуле шығару. Планк формуласы. Кирхгоф заңы. Денелердің қыздырған кезде жарық шығаруын температуралық жарық немесе жылулық сәулелену д.а. Жылулық сәулеленудің тепе-теңдік сипатын дененің сәуле шығару нәтижесінде энергиясы қанша кемісе, өзі жұтқан сәулелік энергия мөлшері де сондай болумен түсіндіруге болады. Дененің бетінен бірлік уақытта шығарылатын сәулелік энергия мөлшері дененің сәуле шығарғыштық қабілеті немесе энергетикалық жарқыраушысы д.а. Егер дененің сәуле шығарғыштық қабілеті ( Планктың кванттық болжамы-жарық үздік-үздік, белгілі бір мөлшерде энергия порциялары н/се энергия кванттары түрінде шығарылады(жұтылады) ж/е энергия квант тербеліс жиілігіне пропорционал 66. Электромагниттік тербелістер. Тербелмелі контур.Томсон ф-н қорыту Электромагниттік тербелістер деп, контурдағы тоқ күшінің периодты түрде өзгеру процесін айтамыз. Тоқ күші осы контурдың электрлік ж/е магниттік қасиеттерін сипаттайды. Сыйымдылығы С конденсатордан ж/е индуктивтігі L катушкадан тұратын электр тізбегін тербелмелі контур д.а. Контурдың R кедергісін нөлге тең деп аламыз. Егер конденсаторды потенциалдар айырмасы U –ға дейін
67. Жарықтың жұтылуы мен сейілуі.Жарық дисперсиясы. Ньютон спектрі. Жарықтың жұтылуы – жарық энергиясының затқа енуіне байланысты кемуі. Жарық бір ортадан өткенде оның интенсивтілігі кемиді, өйткені жарықтың электр өрісі зат атомдарының құрамындағы электрондарды еріксіз тербету үшін энергиясын жұмсайды, ол энергияның басқа түріне айналады. Зат атомдарының бір-бірімен соқтығысу нәтижесінде электронның тербеліс энергиясының біраз бөлігі атомның ретсіз қозғалыс энергиясына айналады. Жарық интенсивтілігінің кему дәрежесі жарық өтетін заттың табиғатына ж/е оның қалындығына байланысты. Жұтатын ортада жарық интенсивтілігі экспоненциал заңымен кемиді, ол Бугер-Ламберт заңы деп аталады Дисперсия – ортада тараған жарықтың фазалық жылдамдығының жиілікке байланыстылығы. Фазалық жылдамдық Ньютон сақиналары:Жазық шыны пластинканың үстіне жазық-дөңес линза қойылса, онда олардың арасында ауа қабаты пайда болады.Пластинка бетіне перпендикуляр бағытта, монохромат жарық түссе, онда жарық толқындары ауа қабатының үстіндегі ж/е төменгі шекараларында шағылады да, өзара интенференцияланады, нәтижесінде линза мен пластинка тиісіп тұрған нүктесінде күңгірт дақ пайда болып, оны концентрлі жарық ж/е күнгірт шеңберлер қоршап тұрады.
68 Кристалл ішіндегі электрондардың стационар күйлері.Ферма деңгейі. Азғындалған электрон газы. Азғындалған газ- бөлшектердің жүйесінің қасиеттері классикалық статистика заңдарына бағынатын жүйенің қасиеттерінен өзгеше газ. Мысалы фермиондар мен бозондар газдары.газдардың азғындалуы төменгі температура мен қысымда айқын байқалады. Газдың азғындалу дәрежесін сипаттайтын А=
Суретте (а)f функциясының T=OK графигі берілген. Графиктен T=O K кезінде Ферми деңгейіне дейін энергетикалық деңгейлер бір электронмен толтырылған, ал Ферми деңгейінен жоғары электрондар жоқ. Олай болса ферми деңгейі электрондардың максималдық энергиясын береді. Егер Т>O К және Бұл өрнектен электронның орташа энергиясы энергиясымен шамалас екенін көреміз. Бөлме температурасында электронның жылулық энергиясы 69 Де-Бройл толқынының кейбір қасиеттері. Оның ықтималдық сипаты. Де –Бройл болжамы – кез келген бөлшекті толқын ретінде қарастыруға болады . толқын ұзындығы бөлшектін импульсына байланысты және де Де –Бройл ұзындығы деп аталады. λ=h/P=h/mv. Массасы m бөлшектің v жылдамдықпен еркін қозғалуын қарастырамыз. Ол үшін Де –Бройл толқындаарының фазалық және топтық жылдамдықтарымен есептеп шығарамыз Vфаза = ω/к=ђω/ђk=E/P=mc2 /mv=c2 /v (k=2π/λ -толқын саны) өйткені с>v онда де-Бройл толқындарының фазалық жылдамдығы vфаза>с. Еркін бөлшектер үшін E= dE/dp=pc2/ . W= 70 .Кванттық статистика туралы жалпы мағлұматтар. Боза Эйнштейн бөлінуі. Бозондар. Көп бөлшектен тұратын жүйені статистикалық заңдар арқылы сипаттайды. Статистикалық заңдар классикалық және кванттық болып екіге бөлінеді. Кванттық статитиканың ең бір айырмашылығы бір бөлшекке де қолданылады. Классикалық бөлшектерді бір бірінен ажырата аламыз. Ал кванттық бөлшектерді ажырата алмаймыз. Бөолшектің спиндік сандарына байланысты кванттық статистика екіге бөлінеді. Бозе Эйнштейн және Ферми Дирак. Егер бөлшектін спиндік саны 0-ге немесе бүтін болса, бозондар деп аталып, Боза Эйнштейн тарау занына бағынады. Бозондармен- нөлдік немесе тұтас спиндік бөлшектермен пайда болған бөлшектер жүйелері ұшін кез келген бүтін мәнге 0,1,2... ие болу мүмкін. Бозондардан пайда болған идеал газ – Бозе газ- Бозе-Эйнштейннің кванттық статистикасымен сипатталады. Энергиялар бойынша бозондардың үлестірілуі ,аталған кванттық күйдегі тенбе-тең бозондар саны кез келген болуы мүмкін жағдайдағы Гибстың үлкен канондық үлестіруінен туындайды.
71. Кванттық теория бойынша сутегі атомы. Энергетикалық деңгейлер. Кеңістіктік кванттау. Электрон спині. Паули принципі. Потенциал U(r)=e2z/r тең ядроның центрлік өрісіндегі қозғалатын электронды қарастырайық. Егер z>1 болса сутек тәріздес атом дар, ал z=1 сутегі атомын аламыз. Өріс центрін – симетриялы болғандықтан сфералық кординатта жүйесін қолдануға тиімді. Сфералық координатасындағы Шредингер теңдеуі
Теңдеудің шешімі болу үшін ᴪ функциясы бір орында бір мәнді шектеулі үздіксіз болу керек. Энергияның мәні Еn= - Берілген n үшін l ие мәндерге ие болады l=0,1…n-1. l саны азимуталдық кванттық сан д.а.l cаны электронның орбита бойымен айналу пішіндерінің түрлерін көрсетеді.l=0 болса сопақ эллипс . l=n-1 дөңгелеккеlжақын эллипс. Орбиталды момент импульсінің шамасы кез келген l шамасы Le=ђ Үшінші кванттық сан магниттік кванттық сан деп mәріпімен белгілейміз. Ол берілген l үшін – l мен l аралығында жатады. Мәні L=mђ Электронның спині. Магнит өрісінде атомдар деңгейінің жіктелуін бірінші рет Штерн мен Герлах зертеген.Тәжірибеде атомдар шоғы бір текті емес магнит өрісінен өткізілген.Бұндай магнит F=ϻdB/dz күш әсер етеді. Егер сутегі атомы S күйінде болғанда (l=0) магнит моменті 0-ге тең. Орбиталды моменті сияқты спиндік кванттық санын S деп және 2S+1 энергетикалық күйінде бола алады.Электронның меншікті импульс моментінің шамасы M=ђ немесе одан да көп электрондар бір мезгілде бір күйде бола алмайды.Паули принципі элементтердің электрондық конфигурациясын құрғанда 72.Айнымалы электр тогы. Айнымалы тоқ үшін Ом заңын векторлық диаграмма арқылы қорыту. Электромагнит индукция заңынан магнит ағыны уақыт бойынша өзгерсе айнымалы э.қ күші пайда болады. Ԑ= -
tg Сонымен, тізбектің ұштарындағы кернеу U= 73.Атом ядросының масса ақауы ж/е байланыс энергиясы. Ядроның тыныштық массасы Энергия мен массаның өзара байланысы Эйнштейн формуласымен анықталады Мұны байланыс энергиясы деп атайды. Меншікті байланыс энергия деп, ядроның бір нуклонына сәйкес келетін байланыс энергиясын айтады. Меншікті байланыс энергиясының атомдық санына байланыстылығы 41 суретте көрсетілген. Бұл суретте жеңіл ядролар (A˂20) мен ауыр ядроларының (A˃200) меншікті байланыс энергиясы аз 20÷200 аралығында жатқан ядролар. Бұдан жеңіл ядролар өзара біріккенде, ал ауыр ядролар ыдырағанда пайда болатын жаңа ядролардың байланыс энергиясы кемитінін байқаймыз. Берілген суреттен жеңіл ядролар үшін меншікті байланыс энергиясы тез өседі. Одан кейінгі элементтердің меншікті байланыс энергиясы баяу өсіп, темір элементінен уранға дейін тұрақты болып, ары қарай төмендейді. Бұдан жеңіл ядролар синтезделіп, ауыр ядролар ыдырағанда, бөлініп шығатын энергиялар мәні көбірек болады. 74.Толқындардың суперпозиция принципі. Топтық жылдамдық пен фазалық жылдамдықтар. Дисперсия. Толқындардың суперпозиция принципі- егер ортада бір мезгілде бірнеше толқын тараса онда орта бөлшектерінің тербелісі, әрбір толқын жеке-жеке тараған кезде бөлшектер жасайтын тербелістің векторлық қосындысына тең. Бұдан толқындар бірін бірі ұйытқытпай, бір бірімен қабаттасады. Кез келген күрделі толқында жиіліктері әр түрлі синусоидалық толқындардың қосындысынан тұрады, екінші сөзбен айтқанда топтық толқыннан немесе толқындық пакет ретінде қарастыруға болады. Бұл толқындар жиіліктерінің жиынтығы спектр деп аталады. Дисперсия болмайтын ортада синусоидалдық толқындардың фазалық жылдамдықтары жиіліктеріне байланысты емес, сондықтан фазалық жылдамдықтары бірдей. Олай болса күрделі толқынның таралу кезінде пішіні өзгермейді. Дисперсия құбылыс байқалатын ортада фазалық жылдамдықтары жиілікке тәуелді болғандықтан, жиіліктері әр түрлі синусоидалдық толқындар әр түрлі жылдамдықпен тарайдыԑ= Толқынның топтық жылдамдығы U кез келген берілген толқын амплитудасын таралу жылдамдығын алуға болады. М нүктесінің қозғалыс заңы
Егер Дисперсия- ортада тараған жарықтың фазалық жылдамдығының жиілікке байланыстылығы. Фазалық жылдамдық 75 Өздік және өзара индукция.Ленц ережесі Өздік индукция–кез-келген контурда уақыт бойынша өзгеретін электр тогы уақыт бойынша өзгеретін магнит индукциясын туғызады.демек контурда э.қ күшті индукцияланады Ԑ=-dɸ/dt=-LdI/dt Бұдан Ф=LI екенін көреміз, бұндағы L- контурдың индуктивтілігі. Ленц ережесі –индуктивтілік токтан пайда болған В´ магнит индукциясының бағыты әрқашанда өзін тудырған В магнит индукциясына қарама қарсы.Уақыт бойынша өзгеретін В магнит өрісі контурды қиып өткенде,пайда болған индукциялық ток В´ индукциялық магнит өрісін туғызады.қамтитын контурда оның бағыты сыртқы өрістің бағытына қарама карсы. Оң винт ережесінің индукциялық токтың бағыты сағат тілінің бағытымен бағытталған,ал э.қ күш оң бағыты сағат тілінің бағытына қарсы бағытын аламыз.олай болса э.қ күшінің бағыты мен dФ/dt магнит ағынының өзгерту жылдамдығының бағытына қарама қарсы. Өз ара индукция –контурдың біреуінде ток күші өзгерген кезде оның екіншісінде э.қ күші пайда болу құбылысы.
76Тікбұрышты потенциалдық шұңқыр ішіндегі бөлшек.Туннельді эффект Кванттық және классикалық физикалардың айырмашылығын көрсететін тунельдік эффект болып табылады.классикалық механикада егер бөлшектің энергиясы тосқауыл энергиясынан аз болса бөлшек тосқауылдан өте алмайды, ал кванттық физикада өту ықтималдылығы бар. Бұл бөлшектің толқындық қасиетімен түсіндіріледі. U биіктігі, d ені болатын потенциалдық тосқауылдың сол жағынан келіп түсетін бөлшекті қарастырайық.сурет
Бөлшектің энергиясы тосқауыл потенциялының энергиясынан кем Е<U. Шұңқыр ішіндегі бөлшек үшін Шредингер теңдеуін жазайық
Осы екі дифференциалдық теңдеулердің шешімі I –аймақ үшін х<0, II- аймақ үшін 0<Х<d III – аймақ үшін х>dᴪ3(x)= Мұндағы К1= A1 Х=a шекарасынан шағылған толқын 77. Өзара перпендикуляр бағытталған тербелістерді қосу.Лиссажу фигура X ж/е Y координата өстерінің бойымен жиіліктері бірдей екі тербелістерді қосайық. Бастапқы фазасы нөлге тең бірінші тербелістің теңдеуі 1.Фазалар айырмасы 2. Лиссажу фигуралары: Өзара тербелістердің жиіліктері әр түрлі болса, онда қорытқы тербелістің траекториясы Лиссажу фигураларын береді. Фазалар айырмасы
78.Жарық дифракциясы. Гюгейнс-Френель принципі. Френель зоналары, олардың қолданылуы. Жарықтың дифракциясы-жарық толқындардың өлшемі толқын ұзындығымен шамалас тосқауылды орап өту құбылысы, яғни жарықтың түзу сызықты тараудан ауытқу құбылысы. Жарықтың дифракциясы оның толқындық қасиетін дәлелдейді және Гюгейнс-Френель принципі бойынша түсіндіріледі. Гюгейнс-Френель принципі-толқындық беттін алдыңғы жағындағы әр нүктесіндегі тербелістерді табу үшін, сол нүктеге толқындық беттің барлық элементтерінен келген тербелістерді тауып, олардың амплитудалары мен фазаларын ескере отырып, зара графиктік тәсілмен қосу керек. Френель зоналары. S0 жарықтың көзінен шыққан толқынның М нүктесіндегі әсерін табайық. S көзінен таралған жарық толқындары сфералық толқындық бетер түзейді,сол беттің біреуі S болсын.
Френель осы толқындық бетті ойша дөңгелек зоналарға бөлген. Көршілес жатқан зоналардың М нүктесіндегі тербеліс фазалары қарама-қарсы, олай болса көршілес сфералар радиустарының бір-бірінен айырмасы 79.Жартылай өткізгіштердің қоспалы өткізгіштігі. Жартылай өткізгіштің өткізгіштігіне қоспа үлкен әсер етеді. Мысалы ретінде Ge атомдарын қарастырайық. Германий атомында төрт валентті электрон бар. Атомдар ковалентті байланыста болады. Егер германий кристалды торына бес валентті сурьма атомын енгізсек, онда оның төрт электроны ковалентті байланыс болып, ал бесінші электрон ядродаға нашар тартылып еркін электрон болады. Мұндай қоспаны электрондық н/е n-типтес жартылай өткізгіштік деп аталады. Қоспа атомын ендіру германий атомының кеңістік торының өрісін өзгертіп, тыйым салынған зонаның ішінде қосымша энергетикалық деңгейін туғызады. Оны донорлық деңгей деп, ал қопспа атомдарын донорлық атом дейді. Бұл энергияның шамасы тыйым салынған зонаның энергиясынан әлдеқайда аз, яғни Кристалдың германий торына үш валентті индий атомын енгізейік. Бұл жағдайда толық ковалентті байланыс жасау үшін бір электрон жетіспейді. Жүйеде кемтік пайда болады, электр өткізгіштігі кемтіктер қозғалысынан жасалады, сондықтан оның кемтіктік өткізгіштігі болады да, р-типтес жартылай өткізгіш деп аталады. Металдарда τ электронның еркін жолының орташа уақыты температура өскен сайын азаяды да, кедергі көбееді, ал концентрациясы өзгермейді. Меншікті жартылай өткізгіште экспоненциалды түрде өзгеретін концентрацияның өзгеруі әлдеқайда басым болады. Сондықтан температура өскенде таза жартылай өткізгіштің электр өткізгіштігі тік өседі. Қоспалы жартылай өткізгіште концентрациясының температураға байланыстылығы күрделірек. Температура жоғарлағанда, қоспа концентрациясы жылдам қанығу мәніне жетеді. Бұл барлық донор электрондар босалып немесе акцептор децгейлері электронмен толтырылады. Сонымен қатар температура өскен сайын жартылай өткізгіштің меншікті де электр өткізгіштігі өз үлесін қоса бастайды, электрондар валентті зонадан өткізгіш зонасына көшеді. Сөйтіп үлкен температурада жартылай өткізгіштің өткізгіштігі қоспа және меншікті өткізгіштен тұрады. Төменгі температурада тек қана қоспа өткізгіштігі болады. 80.Фотоэффект заңдары. Эйнштейннің фотоэффектке арналған теңдуі Фотоэффект-жарықтың әсерінен заттан электрондардың бөлініп шығу құбылысы. Фотоэффект құбылысын Леонард Столетов зерттеген. Ол анод және катод электродтар бар, ішінен ауасы сорылған шыны түтікті ток көзіне қосқан. Тізбектегі фототок гальванометр, электродтар арасындағы потенциалдар айырмасы вольтметрмен өлшенген. Анод пен катод арасындағы кернеу потенциометр арқылы өзгертіліп отырған. Жарық әсерінен катодтан бөлініп шыққан электрондар, үдетуші потенциалдар салдарынан анодқа келіп түседі. Катодқа әсер етуші жарықтың спектрлік құрамы және оның интенсивтілігі өзгермесе, онда фотоэлектрондар тогының потенциалдар айырмасына тәуелділігін аламыз, яғни I=f(U), оны вольт-амперлік сипаттамасы дейді. Ал фототокты нөлге айналдыру үшін тежеуші теріс потенциал ( 1)фотоэлектрондардың алғашқы максимал жылдамдығы фотокатодқа түскен жарықтың интенсивтілігіне тәуелдң болмай, тек жарықтың тербеліс жиілігіне байланысты анықталады; 2)бірлік уақыт ішінде катодтан бөлініп шыққан фотоэлектрондар саны түскен жарықтың интенсивтілігіне пропорционал; 3)кез-келген заттың әліде болса фотоэффекті құбылысын қоздыра алатын жарық жиілігі фотоеффектінің қызыл шегі деп атайды. Осы заңдылықтар үшін Эйнштейн формуласы 81 .Дифракцилық тор. Голография принципі. Дифракцилық тор-бірдей өзара параллель орналасқан саңылаулар жиынтығы. Мөлдір саңылаудын енін b, ал мөлдір емес а деп белгілесек, дифракциялық тордың периоды d=b+a өрнегімен анықталады. Торға перпендикуляр түскен толқынның дифракциясын қарастырайық.
Суреттен екі шеткі сәулесінің жол айырмасы Δ=dsin |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1254. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
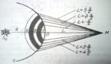
 Комптон тәжірибесі суретте көрсетілген. Рентген сәулесі затқа түсіп шашырайды, шашыраған толқындар ұзындығын D спектрометр арқылы анықтайды. Бұл тәжірибеден толқын ұзындығын λ түскен сәулесімен қатар толқын ұзындығы
Комптон тәжірибесі суретте көрсетілген. Рентген сәулесі затқа түсіп шашырайды, шашыраған толқындар ұзындығын D спектрометр арқылы анықтайды. Бұл тәжірибеден толқын ұзындығын λ түскен сәулесімен қатар толқын ұзындығы  болатын басқа сәуленің бар екені байқалады. Толқын ұзындықтарының айырмасы
болатын басқа сәуленің бар екені байқалады. Толқын ұзындықтарының айырмасы  шашыратқыш затқа ж/е түскен сәуленің толқынының ұзындығына тәуелді болмай, тек шашыраған сәулелердің шашырау боғытына байланысты
шашыратқыш затқа ж/е түскен сәуленің толқынының ұзындығына тәуелді болмай, тек шашыраған сәулелердің шашырау боғытына байланысты 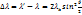 . Мұндағы
. Мұндағы  м – комптон толқын ұзындығы,
м – комптон толқын ұзындығы,  шашыраған сәуленің толқын ұзындығы
шашыраған сәуленің толқын ұзындығы 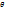 -шашырау бұрышы.
-шашырау бұрышы. , егер
, егер  деп белгілесек
деп белгілесек  интеграл мәні
интеграл мәні  осы сияқты кемтіктер концентрациясы
осы сияқты кемтіктер концентрациясы  Меншікті жартылау өткізгіштігіне өткізгіш зонасына өткен электрон валентті зонада кемтік қалдырады, олай болса электрондар мен кемтіктер концентрациясы тең
Меншікті жартылау өткізгіштігіне өткізгіш зонасына өткен электрон валентті зонада кемтік қалдырады, олай болса электрондар мен кемтіктер концентрациясы тең  . Жалпы концентрациясы
. Жалпы концентрациясы  мәндерін қойсақ
мәндерін қойсақ  ,
, 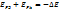 екенін ескерсек
екенін ескерсек  мұндағы
мұндағы  рұқсат етілмеген зонаның ені. ЖӨ-ң меншікті өткізгіштігі
рұқсат етілмеген зонаның ені. ЖӨ-ң меншікті өткізгіштігі  мұндағы
мұндағы  – электронмен кемтіктің қозғалғыштығы. Қозғалыстың
– электронмен кемтіктің қозғалғыштығы. Қозғалыстың  ал
ал  сондықтан
сондықтан  немесе
немесе 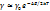 Берілген формуладан өткізгіштік температура б-ша экспонент заңымен өзгереді. Температура өскенде жылдам өседі. Егер
Берілген формуладан өткізгіштік температура б-ша экспонент заңымен өзгереді. Температура өскенде жылдам өседі. Егер  -ның
-ның  бойынша графигін сызсақ түзу аламыз. Ферми деңгейін
бойынша графигін сызсақ түзу аламыз. Ферми деңгейін 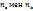 мәндерін теңестіру арқ табамыз
мәндерін теңестіру арқ табамыз  бұдан
бұдан  Екінші мүшесінің мәні өте аз, оны ескермесек ж/е Т=0 жағдайында
Екінші мүшесінің мәні өте аз, оны ескермесек ж/е Т=0 жағдайында  . Ферми деңгейі рұқсат етілмеген зонаның жартысында жатады.
. Ферми деңгейі рұқсат етілмеген зонаның жартысында жатады. ) спектрлік аралықтың бір алқабына есептелінсе, оны дененің спектрлік сәуле шығарғыштық қабілеті
) спектрлік аралықтың бір алқабына есептелінсе, оны дененің спектрлік сәуле шығарғыштық қабілеті  деп атайды.
деп атайды.  Егер дене мөлдір болмаса, онда дене бетіне түскен сәулелік энергияның біраз бөлігі жұтылады. Осы жұтылған энергияның түскен энергияға қатынасы дененің сәуле жұтқыштық қабілеті д.а. Сонда толқындар ұзындығы λ және λ+dλ аралығында сәулелер энергиясының белгілі температурада дененің беті жұтқан бөлігін көрсететін шама дененің спектрлік сәуле жұтқыштық қабілеті
Егер дене мөлдір болмаса, онда дене бетіне түскен сәулелік энергияның біраз бөлігі жұтылады. Осы жұтылған энергияның түскен энергияға қатынасы дененің сәуле жұтқыштық қабілеті д.а. Сонда толқындар ұзындығы λ және λ+dλ аралығында сәулелер энергиясының белгілі температурада дененің беті жұтқан бөлігін көрсететін шама дененің спектрлік сәуле жұтқыштық қабілеті  д.а. Егер дене бетіне түскен сәулелік энергияны талғамай толық жұтатын болса, онда ондай дене абсолют қара дене д.а. Неміс ғылымы Кирхгоф 1895 жылы термодинамика заңдарына сүйеніп, дененің сәуле шығарғыштық қабілетінің
д.а. Егер дене бетіне түскен сәулелік энергияны талғамай толық жұтатын болса, онда ондай дене абсолют қара дене д.а. Неміс ғылымы Кирхгоф 1895 жылы термодинамика заңдарына сүйеніп, дененің сәуле шығарғыштық қабілетінің 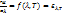 . Осы қағида Кирхгоф заңы д.а.
. Осы қағида Кирхгоф заңы д.а. . Статистика заңдарын қолдана отырып кванттық осциллятордың орташа энергиясын қорытып шығарайық. Классикалық физикада энергияның мәні үздіксіз болғандықтан, орташа мәнін іздегенде интегралдық, ал кванттық физикада энергияның мәндері дикрентті болғандықтан, дикрентті деңгейдегі энергияның қосындысын аламыз. ˂
. Статистика заңдарын қолдана отырып кванттық осциллятордың орташа энергиясын қорытып шығарайық. Классикалық физикада энергияның мәні үздіксіз болғандықтан, орташа мәнін іздегенде интегралдық, ал кванттық физикада энергияның мәндері дикрентті болғандықтан, дикрентті деңгейдегі энергияның қосындысын аламыз. ˂  ˃=
˃=  геометриялық прогрессияның қосындысын береді. Онда ˂
геометриялық прогрессияның қосындысын береді. Онда ˂  мұнда
мұнда 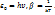 Олай болса ˂
Олай болса ˂  Абсолют қара дененің сәуле шығарғыштық қабілетінің толқын жиілігі мен температураға тәуелдігі былай жазылады:
Абсолют қара дененің сәуле шығарғыштық қабілетінің толқын жиілігі мен температураға тәуелдігі былай жазылады:  ˂
˂  Планк формуласының физикалық мағынасы.Планк формуласына энергия тығыздығы жиіліктің кіші ж/е үлкен мәндерінде нөлге ұмтылады ж/е дененің температурасы өскен кезде энергия максимумы жиіліктің өсу жағына ұмтылады. Бұлай болу себебі Планк формуласы екі көбейткіштен тұрады
Планк формуласының физикалық мағынасы.Планк формуласына энергия тығыздығы жиіліктің кіші ж/е үлкен мәндерінде нөлге ұмтылады ж/е дененің температурасы өскен кезде энергия максимумы жиіліктің өсу жағына ұмтылады. Бұлай болу себебі Планк формуласы екі көбейткіштен тұрады  ж/е
ж/е  зарядымен зарядтасақ, онда конденсатордың разрядталуының нәтижесінде тізбекте I тоғы пайда болады, сөйтіп катушканың ұштарында потенциалдар айырмасына тең өздік индукция
зарядымен зарядтасақ, онда конденсатордың разрядталуының нәтижесінде тізбекте I тоғы пайда болады, сөйтіп катушканың ұштарында потенциалдар айырмасына тең өздік индукция  э.қ.к. пайда болады:
э.қ.к. пайда болады:  . Мұндағы минус таңбасы конденсатордағы потенциалдар айырмасына өздік индукцияның қарсы бағытта болатынын көрсетеді. Бірақ өткізгіштегі электр тоғының ағуы үздіксіз емес, өйткені электр энергиясы 1) шын мәнінде өткізгіштің кедергісі R нөлге тең емес, демек жылулық шығынға; 2) конденсатор диэлектригіндегі шығынға; 3) катушка өзегіндегі гистерезистік шығынға; 4) сәулелену шығындарына және т/б жұмсалады. Сондықтан
. Мұндағы минус таңбасы конденсатордағы потенциалдар айырмасына өздік индукцияның қарсы бағытта болатынын көрсетеді. Бірақ өткізгіштегі электр тоғының ағуы үздіксіз емес, өйткені электр энергиясы 1) шын мәнінде өткізгіштің кедергісі R нөлге тең емес, демек жылулық шығынға; 2) конденсатор диэлектригіндегі шығынға; 3) катушка өзегіндегі гистерезистік шығынға; 4) сәулелену шығындарына және т/б жұмсалады. Сондықтан 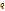 зарядтар конденсатордан катушкаға кешігіңкіреп бір dt уақытта жетеді, өйткені олар өткізгіштер ішінде көптеген кедергілер соқтығысып өтеді. Олай болса, тізбектегі тоқтың мәні барлық емес. Осының әсерінен конденсатор астарларындағы потенциалдар айырмасына U катушканың ұштарына да кешігіп жетуі мүмкін ж/е катушкадағы өздік индукция э.қ.к.
зарядтар конденсатордан катушкаға кешігіңкіреп бір dt уақытта жетеді, өйткені олар өткізгіштер ішінде көптеген кедергілер соқтығысып өтеді. Олай болса, тізбектегі тоқтың мәні барлық емес. Осының әсерінен конденсатор астарларындағы потенциалдар айырмасына U катушканың ұштарына да кешігіп жетуі мүмкін ж/е катушкадағы өздік индукция э.қ.к.  керісінше, қарсы бағытта сонша уақытқа кешігеді. Енді Кирхгофтың екінші ережесін осы жағдайға қолдана отырып, мына теңдеулерді жазайық:
керісінше, қарсы бағытта сонша уақытқа кешігеді. Енді Кирхгофтың екінші ережесін осы жағдайға қолдана отырып, мына теңдеулерді жазайық:  немесе
немесе  . Бұл жағдайда біз
. Бұл жағдайда біз  дейміз, яғни конденсатор диэлектригінде, катушкада ж/е қоршаған кеңістікте электромагниттік энергияның сәулелену шығындары болады дейміз. Мына шарттарды, яғни
дейміз, яғни конденсатор диэлектригінде, катушкада ж/е қоршаған кеңістікте электромагниттік энергияның сәулелену шығындары болады дейміз. Мына шарттарды, яғни  ,
,  ескерсек, онда үстідегі теңдеу мына түрде жазылады:
ескерсек, онда үстідегі теңдеу мына түрде жазылады:  . Осы өрнек электромагниттік еркін тербелістің дифференциалдық теңдеуі д.а. Осы теңдеуді
. Осы өрнек электромагниттік еркін тербелістің дифференциалдық теңдеуі д.а. Осы теңдеуді  мұндағы
мұндағы  - циклдік жиілігі, ол
- циклдік жиілігі, ол  – теңдеуі Томсонформуласы днп аталады.
– теңдеуі Томсонформуласы днп аталады. мұндағы
мұндағы 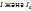 өткен ж/е түскен жарықтың интенсивтілігі, λ-жұтылу коэффициенті, х-заттың қалыңдығы. Мұндағы өткен жарықтың интенсивтілігі, түскен жарықтың интенсивтілігі, жұтылу коэффициенті, заттың қалыңдығы. Жарықтың шашырауы – жарықтың ортадан өткенде ортаның атомдармен әсерлесу салдарынан өзінің бастапқы бағытын өзгертуі. Жарық оптикалық біртекті емес ортада шашырайды, мұндай ортаның сыну көрсеткіші ортаның бір нүктесінен екіншіге көшкенде өзгеріп отырады. Мысал ретінде мөлдір емес орта: эмульсия, түтін, тұман, шаң.
өткен ж/е түскен жарықтың интенсивтілігі, λ-жұтылу коэффициенті, х-заттың қалыңдығы. Мұндағы өткен жарықтың интенсивтілігі, түскен жарықтың интенсивтілігі, жұтылу коэффициенті, заттың қалыңдығы. Жарықтың шашырауы – жарықтың ортадан өткенде ортаның атомдармен әсерлесу салдарынан өзінің бастапқы бағытын өзгертуі. Жарық оптикалық біртекті емес ортада шашырайды, мұндай ортаның сыну көрсеткіші ортаның бір нүктесінен екіншіге көшкенде өзгеріп отырады. Мысал ретінде мөлдір емес орта: эмульсия, түтін, тұман, шаң.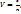 олай болса дисперсия деп заттың сыну көрсеткіші
олай болса дисперсия деп заттың сыну көрсеткіші 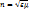 егер ортаның магнит өтімділігін
егер ортаның магнит өтімділігін  десек
десек  . Ортаның диэлектрлі өтімділігі
. Ортаның диэлектрлі өтімділігі 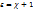 , бұдан
, бұдан  мұндағы
мұндағы  - ортаның диэлектрлік қабылдағышы. Ортаның сыну көрсеткішінің жиілікке байланыстылығын
- ортаның диэлектрлік қабылдағышы. Ортаның сыну көрсеткішінің жиілікке байланыстылығын  мұндағы n
мұндағы n  электрондардың концентрациясы мен бір атомның поляризациясы, ал е мен r электронның заряды мен айналу радиусы. Атомның поляризациясы
электрондардың концентрациясы мен бір атомның поляризациясы, ал е мен r электронның заряды мен айналу радиусы. Атомның поляризациясы  мұндағы
мұндағы  сыртқы түскен жарықтың электр кернеулігі.
сыртқы түскен жарықтың электр кернеулігі.  бұдан
бұдан 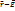 байланысын табуымыз керек. Сыртқы түскен жарықтың әсерінен атомдағы атомдағы электрон еріксіз тербеліс жасайды. Егер сыртқы өріс кернеулігі
байланысын табуымыз керек. Сыртқы түскен жарықтың әсерінен атомдағы атомдағы электрон еріксіз тербеліс жасайды. Егер сыртқы өріс кернеулігі  косинус заңымен өзгеріп, ал ортаның өшу коэффициенті
косинус заңымен өзгеріп, ал ортаның өшу коэффициенті  болса, еріксіз тербелістің теңдеуі
болса, еріксіз тербелістің теңдеуі  түрінде жазылады. Тербеліс теориясынан электронның орныққан еріксіз тербелісі
түрінде жазылады. Тербеліс теориясынан электронның орныққан еріксіз тербелісі  онда
онда 
 Заттың электр қабылдағыштығы
Заттың электр қабылдағыштығы 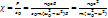 сондықтан
сондықтан  , мұны дисперсия формуласы д.а. Берілген формуладан жиілік –ден
, мұны дисперсия формуласы д.а. Берілген формуладан жиілік –ден 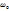 дейін өзгергенде сыну көрсеткіші n(0) – ден монотонды
дейін өзгергенде сыну көрсеткіші n(0) – ден монотонды  дейін өседі, резонанс кезінде таңбасы секірмелі түрде өзгереді. Жиілікті ары қарай өсірсек
дейін өседі, резонанс кезінде таңбасы секірмелі түрде өзгереді. Жиілікті ары қарай өсірсек 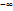 -тен 1-ге дейін монотонды өседі.
-тен 1-ге дейін монотонды өседі. Олар центрден қашықтаған сайын жиілей береді, оны Ньютон сақиналары деп атайды.Жолдың оптикалық айырмасы
Олар центрден қашықтаған сайын жиілей береді, оны Ньютон сақиналары деп атайды.Жолдың оптикалық айырмасы  . Егер жарық нормальді түссе sin(i)=0 ж/е сыну көрсеткіші n=1 болса
. Егер жарық нормальді түссе sin(i)=0 ж/е сыну көрсеткіші n=1 болса  Екі пластинканың қиылысқан ұштарынада d=0 болып,
Екі пластинканың қиылысқан ұштарынада d=0 болып,  интенференция жолақтары күңгірт болады. Бірінші ақ жолақ k=1,
интенференция жолақтары күңгірт болады. Бірінші ақ жолақ k=1,  ауаның қалыңдығы
ауаның қалыңдығы  , екінші ақ жолақта
, екінші ақ жолақта 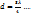 Өткінші жарықта Ньютон жарық сақиналарының радиустары
Өткінші жарықта Ньютон жарық сақиналарының радиустары 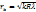 , (k-0,1,2,3…), қараңғы сақиналарының радиустары
, (k-0,1,2,3…), қараңғы сақиналарының радиустары  Мұндағы R- линзаның қисықтығының радиусы.Шағылған жарықтың Ньютонның жарық сақиналарының радиустары
Мұндағы R- линзаның қисықтығының радиусы.Шағылған жарықтың Ньютонның жарық сақиналарының радиустары 
 болса азғындалған болып есептеледі . енді металдағы электрондық газды қарастырайық. Алдымен газ температурасы Т=0K жағдайын алайық.Электронның спиндері ½ срндықтан Ферми-Дирак статистикасына бағынады.f=1/
болса азғындалған болып есептеледі . енді металдағы электрондық газды қарастырайық. Алдымен газ температурасы Т=0K жағдайын алайық.Электронның спиндері ½ срндықтан Ферми-Дирак статистикасына бағынады.f=1/ 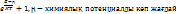 EF әріпімен белгіленіп Ферми деңгейі немесе Ферми энергиясы деп аталады. Егер E< EF болса експонент таңбасы оң теріс болып және Т=0K, жағдайда f→1 ұмтылады. Егер Е> EF болса експонент таңбасы оң болып және Т=0K, f→0
EF әріпімен белгіленіп Ферми деңгейі немесе Ферми энергиясы деп аталады. Егер E< EF болса експонент таңбасы оң теріс болып және Т=0K, жағдайда f→1 ұмтылады. Егер Е> EF болса експонент таңбасы оң болып және Т=0K, f→0
 болғанда f=1/2 Ферми деңгейі ықтимал толтырылуы, ½ деңгейімен сәйкес келеді. Температурасы T=0 K мен Т>O К функциясының айырмашылықтары аз, тек kT ретті аймақта ғана байқалады. Олай болса Ферми-Дирак таралу функциясы температураға аса тәуелді емес екенін көрсетеді. Демек, жылулық қозғалыс барлық электрондардың тек аз ғана бөлігіне әсер етеді. Сондықтан электрондардың орташа энергиясы температураға тәуелділігі әлсіз болады. Электронның абсолют нөл температурасының орташа энергиясы
болғанда f=1/2 Ферми деңгейі ықтимал толтырылуы, ½ деңгейімен сәйкес келеді. Температурасы T=0 K мен Т>O К функциясының айырмашылықтары аз, тек kT ретті аймақта ғана байқалады. Олай болса Ферми-Дирак таралу функциясы температураға аса тәуелді емес екенін көрсетеді. Демек, жылулық қозғалыс барлық электрондардың тек аз ғана бөлігіне әсер етеді. Сондықтан электрондардың орташа энергиясы температураға тәуелділігі әлсіз болады. Электронның абсолют нөл температурасының орташа энергиясы 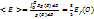
 эВ, олай болса тек Ферми деңгейіндегі электрондар қози алады, қалғандары қоздыру кезінде энергиялары өте аз. Сондықтан көп процестерде электрондардың аз бөлігі ғана қатысады. Металдардың жылулық сыйымдылығын түсіндіруде электрондардың қосатын үлесі өте аз. Ферми энергиясының температураға байланысты формуласы:
эВ, олай болса тек Ферми деңгейіндегі электрондар қози алады, қалғандары қоздыру кезінде энергиялары өте аз. Сондықтан көп процестерде электрондардың аз бөлігі ғана қатысады. Металдардың жылулық сыйымдылығын түсіндіруде электрондардың қосатын үлесі өте аз. Ферми энергиясының температураға байланысты формуласы:  .
.
 . Ықтималдықты нормалау шарты
. Ықтималдықты нормалау шарты 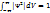 .
. Осы үлестіру Бозе Эйнштейн үлестіру деп аталады. ϻ-Энергияға тәелді емес, бөлшектер санының тығыздығымен және температурамен ғана анықталады химиялық потенциал.
Осы үлестіру Бозе Эйнштейн үлестіру деп аталады. ϻ-Энергияға тәелді емес, бөлшектер санының тығыздығымен және температурамен ғана анықталады химиялық потенциал. (r2
(r2 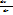 )+
)+  +
+  =
=  =Eᴪ
=Eᴪ .Яғни Бор теориясымен сәйкес болады n бас квант саны,мәні n=1,2…
.Яғни Бор теориясымен сәйкес болады n бас квант саны,мәні n=1,2…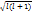
 =ђ
=ђ 
 . Анымалы тоқ алу үшін, тұрақты бұрыштық жылдамдықпен айналатын рамканы магнит өрісіне еңгізуіміз керек. Кез келген уақыт мезетінде рамка орамының ауданың тесіп өтетін магнит ағыны
. Анымалы тоқ алу үшін, тұрақты бұрыштық жылдамдықпен айналатын рамканы магнит өрісіне еңгізуіміз керек. Кез келген уақыт мезетінде рамка орамының ауданың тесіп өтетін магнит ағыны  Олай болса Ԑ= -
Олай болса Ԑ= -  мұндағы
мұндағы 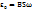 , Ом заңынан I=
, Ом заңынан I=  . Айнымалы тоқтын әсерлік және максимал мәндері мынандай қатынаста болады
. Айнымалы тоқтын әсерлік және максимал мәндері мынандай қатынаста болады 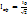 ,
,  . Айным алы тоқ тізбегіндегі кедергі, индуктивтілік және сыйымдылық Ом заңы. Активті кедергіден, индуктивтіліктен және сыйымдылықтан тұратын тізбекті қарастырайық. Тізбекке
. Айным алы тоқ тізбегіндегі кедергі, индуктивтілік және сыйымдылық Ом заңы. Активті кедергіден, индуктивтіліктен және сыйымдылықтан тұратын тізбекті қарастырайық. Тізбекке  жиілігі бар кернеу тудырайық U=
жиілігі бар кернеу тудырайық U=  cos
cos  Активті кедергіде тоқ пен кернеу арасында ығысу фазасы жоқ ; сондықтан I=
Активті кедергіде тоқ пен кернеу арасында ығысу фазасы жоқ ; сондықтан I= 

 индуктивтілігі кернеудің кемуі токтың фазасы жағынан
индуктивтілігі кернеудің кемуі токтың фазасы жағынан  озады, ал(
озады, ал(  ) –
) –  cos(
cos( 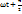 ),
),  сыйымдылықта U=
сыйымдылықта U=  . Бұндай жүйенің векторлық диаграммасы көрсетілген. Суреттен тізбектің кернеуі мен ток күшінің фазалық айырмасы
. Бұндай жүйенің векторлық диаграммасы көрсетілген. Суреттен тізбектің кернеуі мен ток күшінің фазалық айырмасы 
 ,
,  - кернеулер кемуінің қосындысы тізбекке түсірілген U кернеуге тең болу керек. Суреттен
- кернеулер кемуінің қосындысы тізбекке түсірілген U кернеуге тең болу керек. Суреттен  2+
2+ 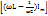 2 бұдан айнымалы тізбек үшін Ом заңы
2 бұдан айнымалы тізбек үшін Ом заңы 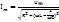 , мұндағы
, мұндағы  тізбектің толық кедергісі және
тізбектің толық кедергісі және 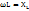 ,
,  , екенін ескерсек X=
, екенін ескерсек X= 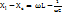 мұны реактивті кедергі деп атайды.
мұны реактивті кедергі деп атайды. заңдылығымен өзгеретін болса, ток I=
заңдылығымен өзгеретін болса, ток I= 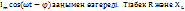 кедергілерінен тұрса tg
кедергілерінен тұрса tg  , ал R мен
, ал R мен  кедергілерінен тұрса tg
кедергілерінен тұрса tg  токтары
токтары  ,
, әрқашан оны құраушы нуклондардың массаларының қосындысынан кем болады, оның шамасы
әрқашан оны құраушы нуклондардың массаларының қосындысынан кем болады, оның шамасы 




 олай болса
олай болса  топтық жылдамдықтың формуласы. Топтық жылдамдық пен фазалық жылдамдықтың арасындағы байланыс.
топтық жылдамдықтың формуласы. Топтық жылдамдық пен фазалық жылдамдықтың арасындағы байланыс. ,
,  өрнегін дифференциялдайық
өрнегін дифференциялдайық 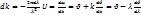
 болса қалыпты дисперсия (U˂V), ал
болса қалыпты дисперсия (U˂V), ал 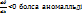 дисперсия деп аталады,
дисперсия деп аталады,  =0 дисперсия болмайтын орта (U=V).
=0 дисперсия болмайтын орта (U=V). , олай болса дисперсия деп заттың сыну көрсеткішінің жиілікке байланыстылығын айтады. Сыну көрсеткіші
, олай болса дисперсия деп заттың сыну көрсеткішінің жиілікке байланыстылығын айтады. Сыну көрсеткіші  Ортаның диэлектрлік өтімділігі ԑ=x+1, бұдан
Ортаның диэлектрлік өтімділігі ԑ=x+1, бұдан  мұндағы x-ортаның диэлектрлік қабылдағышы.
мұндағы x-ортаның диэлектрлік қабылдағышы.



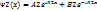

 , K2=
, K2= 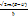
 және
және 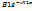 тосқауылға түсетін ,шағылатын де Бройль толқындары.
тосқауылға түсетін ,шағылатын де Бройль толқындары. 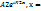 0 шекарасынан сынып өткен толқын, ал
0 шекарасынан сынып өткен толқын, ал 
 тосқауылдан өтіп қайта оралмайтын толқын. Тосқауыл мен бөлшектің айырым энергиясы U~E мен тосқауылдың ені көп болып және бөлшектің массасы ауырлау болса өту ықтималдығы аз болады. Бөлшек энергиясының тосқауыл биіктігінің энергиясынан аздығына қарамастан тосқауылды өту құбылысы тунелдік эффект д.а
тосқауылдан өтіп қайта оралмайтын толқын. Тосқауыл мен бөлшектің айырым энергиясы U~E мен тосқауылдың ені көп болып және бөлшектің массасы ауырлау болса өту ықтималдығы аз болады. Бөлшек энергиясының тосқауыл биіктігінің энергиясынан аздығына қарамастан тосқауылды өту құбылысы тунелдік эффект д.а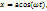 екіншісі y=bcos(
екіншісі y=bcos(  ). Бірінші теңдеуден cos
). Бірінші теңдеуден cos  және
және  =
=  . Онда
. Онда  . Түрлендіруден кейін
. Түрлендіруден кейін 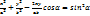 бұл эллипстің теңдеуі. Кейбір жағдайлардағы тербеліс траекториясының пішінін қарастырайық
бұл эллипстің теңдеуі. Кейбір жағдайлардағы тербеліс траекториясының пішінін қарастырайық болса,
болса, 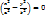 бұдан
бұдан  түзудің теңдеуі шығады, “+”таңбасы m-мәні жұп болып, тербелістердің фазалары бірдей, ал “-” таңбасы m-мәні тақ болып, фазалары қарама-қарсы болады. Қорытқы тербелістің амплитудасы
түзудің теңдеуі шығады, “+”таңбасы m-мәні жұп болып, тербелістердің фазалары бірдей, ал “-” таңбасы m-мәні тақ болып, фазалары қарама-қарсы болады. Қорытқы тербелістің амплитудасы  ,
,  . Тербелелісті сызықты поляризацияланған деп атайды.
. Тербелелісті сызықты поляризацияланған деп атайды. , тербеліс теңдеуі былай жазылады
, тербеліс теңдеуі былай жазылады  Эллипс өстері ОX ж/е ОY өстеріне сәйкес келеді. Егер a=b болса эллипс шеңберге айналады. Тербелісті дөңгелек бойынша поляризацияланған деп айтады.
Эллипс өстері ОX ж/е ОY өстеріне сәйкес келеді. Егер a=b болса эллипс шеңберге айналады. Тербелісті дөңгелек бойынша поляризацияланған деп айтады. 
 , ал жиіліктер қатынастары
, ал жиіліктер қатынастары  болатын тербелістердің траекториясы берілген.
болатын тербелістердің траекториясы берілген.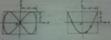
 –ге тең. М нүктесіндегі қорытқы тербелістердің амплитудасы А=А0-A1+A2-A3+...,(9) мұндағы А0-орталық зонадан, ал A1-бірінші, A2-екінші және одан кейінгі зоналардан келген толқындар амплитудасы. Қатарлас жатқан зоналардың амплитудалары бір-бірінен айырмашылықтары аз болғандықтан, сызықты өзгереді деп алуымызғы болады, сондықтан
–ге тең. М нүктесіндегі қорытқы тербелістердің амплитудасы А=А0-A1+A2-A3+...,(9) мұндағы А0-орталық зонадан, ал A1-бірінші, A2-екінші және одан кейінгі зоналардан келген толқындар амплитудасы. Қатарлас жатқан зоналардың амплитудалары бір-бірінен айырмашылықтары аз болғандықтан, сызықты өзгереді деп алуымызғы болады, сондықтан  (10), олай болса М нүктесіндегі қорытқы тербелістің амплитудасы
(10), олай болса М нүктесіндегі қорытқы тербелістің амплитудасы  (11). (9)ж/е (10) формулалар бойынша жақша ішіндегі амплитудалар қосындысы нольге тең. Демек, интерференция салдарынан өте көп зоналардың қорытқы тербелістерінің амплитудасы орталық зонаның әсерінен пайда болған тербеліс амплитудасының жартысына тең. Олай болса бір текті ортада еркін тараған жарық М нүктесінде түзу сызықты таралады деп қарастыруға болады.
(11). (9)ж/е (10) формулалар бойынша жақша ішіндегі амплитудалар қосындысы нольге тең. Демек, интерференция салдарынан өте көп зоналардың қорытқы тербелістерінің амплитудасы орталық зонаның әсерінен пайда болған тербеліс амплитудасының жартысына тең. Олай болса бір текті ортада еркін тараған жарық М нүктесінде түзу сызықты таралады деп қарастыруға болады.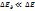 бөлме температуралардың өзін де жылулық қозғалыс энергиясының өзі қоспа деңгейіндегі электрондарды өткізгіш зонаға көтеру үшін жеткілікті.
бөлме температуралардың өзін де жылулық қозғалыс энергиясының өзі қоспа деңгейіндегі электрондарды өткізгіш зонаға көтеру үшін жеткілікті. ). Энергияның сақталу заңынан
). Энергияның сақталу заңынан  , бұдан электрондардың максималдық жылдамдығын табуға болады.Үдетуші потенциалдар айырмасын артқанда фототок артады,потенциалдың мәні бір белгілі шамаға жеткенде қанығады. Өткені катодтан шыққан электрондар түгелімен анодқа жетеді, олай болса қанығу фототогы фотоэлектрондардың санымен анықталады.Осы тәжірбиеден сыртқы фотоэффект құбылысы үшін мынандай үш заң тағайындалды:
, бұдан электрондардың максималдық жылдамдығын табуға болады.Үдетуші потенциалдар айырмасын артқанда фототок артады,потенциалдың мәні бір белгілі шамаға жеткенде қанығады. Өткені катодтан шыққан электрондар түгелімен анодқа жетеді, олай болса қанығу фототогы фотоэлектрондардың санымен анықталады.Осы тәжірбиеден сыртқы фотоэффект құбылысы үшін мынандай үш заң тағайындалды: . Қызыл шегі үшін
. Қызыл шегі үшін  онда
онда  бұдан
бұдан  . Электрондардың заттан шығу жұмысы заттың тегі мен оның бетінің күйіне байланысты. Сондықтан әртүрлі заттар үшін фотоэффектінің қызыл шегі әртүрлі.
. Электрондардың заттан шығу жұмысы заттың тегі мен оның бетінің күйіне байланысты. Сондықтан әртүрлі заттар үшін фотоэффектінің қызыл шегі әртүрлі.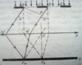
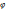 . Дифракцияланған монохромат жарықтың max шарты dsin
. Дифракцияланған монохромат жарықтың max шарты dsin  𝜆, m=0,1,2…
𝜆, m=0,1,2…