
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Металдар мен жартылай откизгиштердеги туйспели кубылыстар. (Зеебек, Пельте кубылыстары, жартылай откизгишти диод)42.Атом ядросы. Ядролық күштер және оның негізгі қасиеттері. Атом ядросындағы нуклондар арасындағы тартылыс күштерін ядролық күштер деп атайды. Оның қасиеттері: 10-15 ара қашықтыққа дейін әсер етеді, қанығу қасиетіне ие, нуклон зарядына байланысты емес. Электромагниттік күштерден 100 есе артық. Центрлік күштер қатарына жатпайды, ол нуклондардың спиндерінің бағытына тәуелді. 43.Күшті, әлсіз, электромагнитті, гравитациялық байланыстар. Қазіргі физика мен астрофизиканыңөзекті мәселелері жөнінде түсінік. 44.Атом ядросының құрылымы. Ядро моделі. Атом ядросы оң зарядталған протоннан және заряды жоқ нейтроннан тұрады. Бұл бөлшектер нуклон деп аталады. Нейтрон: 45.Тізбекті реакция. Ядролық реактор. Синтездеу реакциясы. Энергия көзінің мәселелері. 46.Радиоактивтік ыдырау заңы.Жартылай ыдырау периоды. Радиоактивтік ыдырау түрлері. Радиоактивті құбылыс-атомдардың өздігінен сәуле шығаруы. Радиоактивті сәуле шығаратын заттар қасиеті радиоактивтілік деп аталады.Радиоактивтік элементтердің (уран,торий,радий т.б.) атомдары α,β,ϒ-сәулелерін шығара отырып, басқа бір элемент атомына айналады. Орнықсыз ядролардың белгілі уақыт аралығында орнықты күйге келіп үлгеретін шамасын көрсететін заңдылықты радиоактивтік заңдылықты радиоактивті ыдырау заңы атайды. Егер радиоактивтік ядроның алғашқы саны N0 болса, онда dt уақыт ішінде ыдырап үлгерген ядроның саны dN=-𝜆Ndt, мұндағы 𝜆-ыдырау тұрақтысы.  Ығысу ережесі:
α-бөлшек гелий ядросы, ыдырау формуласы β-бөлшек электрондар ағыны, ыдырау формуласы ϒ-бөлшек – электромагниттік толқын.
. 47. Элементар бөлшектер мен олардың классификациясы. Элементар бөлшектердің әсерлесу типтері.Элементар бөлшектер дег барлық алғашқы материяны құрайтын,әрі қарай бөлінбейтін бөлшектер.Барлық Э. б бір біріне түрленеді ж.е бұл өзара түрлену олардың өмір сүруінің басты шарты болып табылады. Э. б физикасының дамуы космостық сәулелердің ашылуымен байланысты.Э.бді массасына қарай фотондар , лептондар(жеңіл бөлшектер),мезондар(орташа бөл.),бариондар(ауыр б)Негізінен орнықты(40қа жуық саны) ж.е орнықсыз(200) болып бөлінеді.Спиндік санына байланысты а)егер s=+-1/2тең болса, онда бұл бөлшектер Паули принципіне негізделіп фермиондар д.а.б)егер s=+-1,+-2 болса, онда бозондар д.а 48. Ядроның байланыс энергиясы. Массалық ақау. Атом ядросындағы нуклондар өзара әсер ететіндіктен ядро орнықты түзілген болып есептелінеді.Олай болса,ядроны, массасын өте дәлірек масс спектрометр құралының көмегімен өлшеуге болады.Ол үшін меншікті зарядтары әр түрлі зарядталған бөлшектер шоғының массаларын электр ж.е магнит өрістерінің әсері арқылы өлшейді.Өлшеудің нәтижесінде ядроның тыныштықтағы массасы Мя әрқашан оны құраушы протондар мен нейтрондардың тыныштық массаларының қосындысынан кем болатындығы анықталады. Мя<Zmp+Nmn.Мұның себебі нуклондар массасының біраз бөлігі өзара байланысуға жұмсалады.Осындай массаны массалар ақауы д.а^M=M0-Mя Мұндағы M0 = 49. Кванттык сызыктық гармоникалық оссилятор. гармоникалық оссилятор квазисерпімді күштің әсерінен бір өлшемді қозғалыс жасайтын жүйе.мұндай жүйе көптеген классикалық есептермен кванттық теорияның моделі ретінде қарастырылады.Кәдімгі серіппелі Егер де классикалық механика заңдары бойынша бөлшек потенциялдық шұңқыр координаттары (-xmax+xmax)облысы ішінен шыға алмайды десек кванттық механика теориясы бқлшектің осы облыстан шығып кету ықтималдылығының болуы, толқындық қасиетіне байланысты. 50 Бір жаққа бағытталған екі тербелістерді қосу. Қорытқы тербелістің теңдеуі Бағыттары және жиіліктері бірдей екі гармоникалық тербелістерді қосайық. Х1=
51 Де-Бройл толқынының кейбір қасиеттері. Оның ықтималдық сипаты. Де –Бройл болжамы – кез келген бөлшекті толқын ретінде қарастыруға болады . толқын ұзындығы бөлшектін импульсына байланысты және де Де –Бройл ұзындығы деп аталады. λ=h/P=h/mv. Массасы m бөлшектің v жылдамдықпен еркін қозғалуын қарастырамыз. Ол үшін Де –Бройл толқындаарының фазалық және топтық жылдамдықтарымен есептеп шығарамыз Vфаза = ω/к=ђω/ђk=E/P=mc2 /mv=c2 /v (k=2π/λ -толқын саны) өйткені с>v онда де-Бройл толқындарының фазалық жылдамдығы vфаза>с. Еркін бөлшектер үшін E= dE/dp=pc2/ ᴪ(x,y,z,t) ықтималдық амплитудасы деп аталатын шама ұсынды. Бұл шаманы, сондай ақ толқындық функция деп атайды. Ықтималдық амплитудасы кешенді және W ықтималдылық оның модулінің квадратына пропорционал болуы мүмкін. W ̴ |ᴪ(x,y,z,t)|2 Осылайша толқындық функциялардың көмегімен микро обьектінін күйін сипаттау статистикалық ықтималдық сипатқа ие. Толқындық модулінің квадраты х және х+dx, y+dy, z+dz кординаттарымен аймақты t уақыт мезетінде бөлшектеріндің болу ықтималдығы анықтайды. W= 52 .Кванттық статистика туралы жалпы мағлұматтар. Боза Эйнштейн бөлінуі. Бозондар. Көп бөлшектен тұратын жүйені статистикалық заңдар арқылы сипаттайды. Статистикалық заңдар классикалық және кванттық болып екіге бөлінеді. Кванттық статитиканың ең бір айырмашылығы бір бөлшекке де қолданылады. Классикалық бөлшектерді бір бірінен ажырата аламыз. Ал кванттық бөлшектерді ажырата алмаймыз. Бөолшектің спиндік сандарына байланысты кванттық статистика екіге бөлінеді. Бозе Эйнштейн және Ферми Дирак. Егер бөлшектін спиндік саны 0-ге немесе бүтін болса, бозондар деп аталып, Боза Эйнштейн тарау занына бағынады. Бозондармен- нөлдік немесе тұтас спиндік бөлшектермен пайда болған бөлшектер жүйелері ұшін кез келген бүтін мәнге 0,1,2... ие болу мүмкін. Бозондардан пайда болған идеал газ – Бозе газ- Бозе-Эйнштейннің кванттық статистикасымен сипатталады. Энергиялар бойынша бозондардың үлестірілуі ,аталған кванттық күйдегі тенбе-тең бозондар саны кез келген болуы мүмкін жағдайдағы Гибстың үлкен канондық үлестіруінен туындайды.
53 , Кванттық теория бойынша сутегі атомы. Энергетикалық деңгейлер. Кеңістіктік кванттау. Электрон спині. Паули принципі. Потенциал U(r)=e2z/r тең ядроның центрлік өрісіндегі қозғалатын электронды қарастырайық. Егер z>1 болса сутек тәріздес атом дар, ал z=1 сутегі атомын аламыз. Өріс центрін – симетриялы болғандықтан сфералық кординатта жүйесін қолдануға тиімді. Сфералық координатасындағы Шредингер теңдеуі
Теңдеудің шешімі болу үшін ᴪ функциясы бір орында бір мәнді шектеулі үздіксіз болу керек. Энергияның мәні Еn= - Берілген n үшін l ие мәндерге ие болады l=0,1…n-1. l саны азимуталдық кванттық сан д.а.l cаны электронның орбита бойымен айналу пішіндерінің түрлерін көрсетеді.l=0 болса сопақ эллипс . l=n-1 дөңгелеккеlжақын эллипс. Орбиталды момент импульсінің шамасы кез келген l шамасы Le=ђ Үшінші кванттық сан магниттік кванттық сан деп mәріпімен белгілейміз. Ол берілген l үшін – l мен l аралығында жатады. Мәні L=mђ Cонымен n- энергияны сипаттайтын бас кванттық сан, l -импульс моментін сипаттайтын азимуталдық кванттық сан, m-импульс моментінің сыртқы өріске проекциясын сипаттайтын магниттік кванттық сан. Электронның спині. Магнит өрісінде атомдар деңгейінің жіктелуін бірінші рет Штерн мен Герлах зертеген.Тәжірибеде атомдар шоғы бір текті емес магнит өрісінен өткізілген.Бұндай магнит F=ϻdB/dz күш әсер етеді. Егер сутегі атомы S күйінде болғанда (l=0) магнит моменті 0-ге тең. Орбиталды моменті сияқты спиндік кванттық санын S деп және 2S+1 энергетикалық күйінде бола алады.Электронның меншікті импульс моментінің шамасы M=ђ немесе одан да көп электрондар бір мезгілде бір күйде бола алмайды.Паули принципі элементтердің электрондық конфигурациясын құрғанда 54 Өздік және өзара индукция.Ленц ережесі Өздік индукция –кез-келген контурда уақыт бойынша өзгеретін электр тогы уақыт бойынша өзгеретін магнит индукциясын туғызады.демек контурда э.қ күшті индукцияланады Ԑ=-dɸ/dt=-LdI/dt Бұдан Ф=LI екенін көреміз, бұндағы L- контурдың индуктивтілігі. Ленц ережесі –индуктивтілік токтан пайда болған В´ магнит индукциясының бағыты әрқашанда өзін тудырған В магнит индукциясына қарама қарсы.Уақыт бойынша өзгеретін В магнит өрісі контурды қиып өткенде,пайда болған индукциялық ток В´ индукциялық магнит өрісін туғызады.қамтитын контурда оның бағыты сыртқы өрістің бағытына қарама карсы. Оң винт ережесінің индукциялық токтың бағыты сағат тілінің бағытымен бағытталған,ал э.қ күш оң бағыты сағат тілінің бағытына қарсы бағытын аламыз.олай болса э.қ күшінің бағыты мен dФ/dt магнит ағынының өзгерту жылдамдығының бағытына қарама қарсы. Өз ара индукция –контурдың біреуінде ток күші өзгерген кезде оның екіншісінде э.қ күші пайда болу құбылысы. Сурет
55 Тікбұрышты потенциалдық шұңқыр ішіндегі бөлшек.Туннельді эффект Кванттық және классикалық физикалардың айырмашылығын көрсететін тунельдік эффект болып табылады.классикалық механикада егер бөлшектің энергиясы тосқауыл энергиясынан аз болса бөлшек тосқауылдан өте алмайды , ал кванттық физикада өту ықтималдылығы бар. Бұл бөлшектің толқындық қасиетімен түсіндіріледі. U биіктігі, d ені болатын потенциалдық тосқауылдың сол жағынан келіп түсетін бөлшекті қарастырайық. Бөлшектің энергиясы тосқауыл потенциялының энергиясынан кем Е<U. Шұңқыр ішіндегі бөлшек үшін Шредингер теңдеуін жазайық
Осы екі дифференциалдық теңдеулердің шешімі I –аймақ үшін х<0, II- аймақ үшін 0<Х<d III – аймақ үшін х>dᴪ3(x)= Мұндағы К1= A1 Х=a шекарасынан шағылған толқын 56 Гармоникалық тербелістер, олардың сипаттамалары. Тербелістер-белгілі бір дәрежеде уақыт бойынша қайталанып отыратын процесстер. Гарм.тербелістер-периодты түрде өзгеретін физикалық шамалар уақыт бойынша sin н/е cos заңына сәйкес өзгеретін тербелістер. Х= Xmsin(wt+ф0) н\е X=Xmcos(wt+ф0) Сипаттамалары: Х-тербелістегі физикалық шаманың берілген уақыт кезеңіндегі мәні, Хm-тербеліс амплитудасы, тербелістегі шаманың ең үлкен мәні, wt+ф0-тербеліс фазасаы, берілген уаөыт кезеңіндегі физикалық шаманың мәнін анықтайды, ф0-бастапқы фазасы, t=0 уақыттағы фаза мәні, w-циклдік жиілік 2П уақыт ішіндегі тербеліс саны. Т-тербеліс периоды, бір толық тербеліске кететін уақыт, v-тербеліс жиілігі, бірлік уақыт ішіндегі тербеліс саны. W,v, T-физикалық шаманың қатынастары. W=2пv, T=
57 Шредингер теңдеуі. Шредингердің стационар теңдеуі Кванттық механиканың негізігі теңдеуі болып, толқындық функцияға арналған Шредингердің 1926ж ашқан ұсақ бөлшектер күйін сипаттатйтын теңдеуі жатады. Бұл теңдеу бұрыннан белгілі қатынастардан қорытылып шығарылмай, тек көптеген ғылыми тәжірибелердің нәтижелерінен табылады. Шредингер теңдеуінің жалпы түрі: - Мұндағы h=h/2п=1,05*10-34 Дж*с, m-бөлшектің массасы, U=(x,y,z,t)-күштер өрісіндегі бөлшекте потенциалдық энергиясы, i- жорамал сан, (1) теңдеудегі Ψ функциясы потенциалдық өрістегі бөлшекке әсер ететін күштердің потенциалдық энергиясы арқылы анықталады. Сөйтіп, U потенциалдық энергия уақыт пен кордината фунциясы екендігін байқаймыз, яғни Ψ(х,у,z,t) 58 Механикалық тербелістер. Физикалық маятник тербелісінің периодын қорыту. Тербеліс – белгілі бір дәрежеде уақыт бойынша қайталанып отыратын процестер. Тербелістер: механикалық, электромагниттік, электромеханикалық. Гармоникалық осциллятор – х”+wx=0 теңдеуімен сипатталатын жүйе. Мысалы: математикалық және физикалық маятниктер, пружинаға ілінген жүктің тербелісі, тербелмелі контур. Физикалық маятник – оның инерция центріне дәл келмейтін қозғалмайтын нүкте маңында тербеліс жасайтын қатты дене. Т= 2П/ w, W= 59 Гейзенбергтің анықсыздықтар ара қатынасы. Классикалық физикада траектория бойымен қозғалған дененің кез келген уақытта орны мен импульс мәндері болады. Элементар бөлшектер әлемінде бөлшектердің толқындық қасиеттері болған соң траектория деген түсінік болуы мүмкін емес. Сондықтан физикалық шамалар физикаға қарағанда басқаша қатынаста болады. Мысал ретінде х кординатасы мен Рх физикалық шамалардың қатынастарын қарастырайық. Жазық де Бойль толқыны х осі бойынша тарасын. Бұл жағдайда импульс қандай да болса бір мәнге ие болады. Рх =Pz=0, Py=P. Енді саңылау арқылы орнын тауып көрейік. Саңылаудан өткен кезде электронның орны Берілген теңдеуді Гейзенбергтің анықталмаушылық қатынасы деп атайды. Бұдан координатасын дәл анықтасақ импульстің белгілі мәні болмайды және керісінше. Сөйтіп элементар бөлшектердің орны мен импульсін бір мезгілде мәндері болмайды. Үш координаталары бойынша жазсақ 60 Механикалық тербелістер. Математиткалық маятниктің тербеліс периодын қорыту. Тербеліс – белгілі бір дәрежеде уақыт бойынша қайталанып отыратын процестер. Тербелістер: механикалық, электромагниттік, электромеханикалық боп бөлінеді. Математикалық мамятник – салмақсыз және созылмайтын жіпке ілінген, массасы бір нүктеге жинақталған жүйе.
M = -mglsin «-» таңбасы күш моменті мен бұрыштық ығысуы қарама қарсы. Айналмалы қозғалыс динамикасының негізгі теңдеуінен I 61 Жылулық сәуле шығару. Энергетикалық жарқырау , шығару қасиеттері. Абсолют қара дене, оның сәуле шығару заңдары. Жылулық сәулелену – термодинамикалық тепе теңдік күйде болатын дененің электромагниттік сәуле шығаруы. Тепе теңдік күй сақталу үшін дененің сәуле шығару нәтижесінде энергия қанша кемісе, жұтылатын энергия мөлшері де сондай болуға тиіс. Энергетикалық жарқырау дененің бетінен бірлік уақытта шығарылатын сәулелік энергия. Энергетикалық жарқыраушы температураға тәуелді. Сәулелену әр түрлі жиіліктен түрады, олай болса спектрлік сәуле шығарғыштық қабілеті деген физикалық шама енгізіледі. r= Сәуле жұтқыштық қабілеті - Спектрлік сәуле жұтқыштық қабілеті – толқындар жиілігі v және v+dv аралығындағы сәулелер энергиясының белгілі температурада дененің беті жұтқыш бөлігін көрсететін шама. Абсолют қара дене – дене бетіне түскен энергияны толығымен жұтатын дене. Стефан больцман заңы: абсолют қара дененің толық жарқырауы оның төрт дәрежеленген абсолют температурасына пропорционал – R= 2) Абсолют қара дененің энергетикалық жарқырауының максимал спектрлңк тығыздығы бесінші дәрежелі абсолют температураға пропорционал өседі r=bT5 62Өшетін механикалық тербелістер. Серіппіге ілінген жүктің өшетін тербелісі. Өшу коэффициенті. Өшудің логарифмдік декременті. Беріктілік. Өшетін механикалық тербеліс – ортаның кедергісі салдарынан жүйесінің энергиясы кеміп, уақыт бойынша амплитудасы азайып отыратын тербелістер. Кез келген нақты тербелңс жүйесінде тербеліс өшеді. Механикалықтербелістерде өшу ортаның кедергісі, ал электр тізбектерінде өткізгіштің жылу шығару салдарынан болады. Fr=-rv=-rx’ Fcep=-kx мұндағы r – кдергі коэффициенті, «-» таңбасы fr мен v жылдамдық шамаларының бағыттары қарама қарсы . Ньютонның 2 заңынан: F=-Fcep-F, ma= -kx-rV, a=x”, v=x’ , mx’= -kx – rx 2) mx”+kx+rx’=0 x”+2 B - өшу коэффициенті, w0 – жүйенің меншікті жиілігі Шешімі: x” = a(t)cos(wt+ a(t) – уақыт бойынша кеміп отыратын амплитудасы, оның мәнін үшін х’ және x” туындыларын 2 теңдеуге қойып , түрлендіреміз. Логарифмдік декремент – тербеліс амплитудасы экспоненциал заңымен кемігендіктен, бір периодқа сәйкес уақыт мезетінде амплитудалар қатынасын A=ln Тербелмелі жүйені сипаттау үшін жүйе сапалылығы депаталатын физикалық шаманы еңгіземіз Q |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 639. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
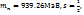 Магнит моменті -1,91
Магнит моменті -1,91 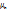 . . Протон:
. . Протон: 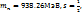 Магнит моменті +2,79
Магнит моменті +2,79 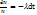 , бұдан N= N0
, бұдан N= N0 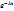 . Бұл радиоактивті ыдырау заңы. Радиоактивті ядролардың жартысы ыдырап үлгеретін уақытты жартылай ыдырау периоды деп атайды. N=
. Бұл радиоактивті ыдырау заңы. Радиоактивті ядролардың жартысы ыдырап үлгеретін уақытты жартылай ыдырау периоды деп атайды. N= 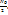 N0
N0 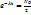 ,
, 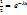 бұдан ln2=𝜆t, T=
бұдан ln2=𝜆t, T= 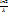 =
= 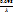 .радиоактивті ядроның орташа өмір сүру уақыты
.радиоактивті ядроның орташа өмір сүру уақыты 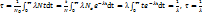 ыдырау тұрақтысына кері шама. Радиоактивті ядроның активтігі A=
ыдырау тұрақтысына кері шама. Радиоактивті ядроның активтігі A= 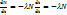 .
.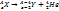 α-ыдырау үшін;
α-ыдырау үшін;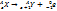 β-ыдырау үшін;
β-ыдырау үшін;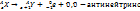 . Бұдан басқа екі ыдырау түрі бар:
. Бұдан басқа екі ыдырау түрі бар: 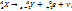 p+
p+ 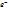 →n+
→n+ 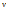 .
.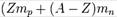 Массалық ақау:
Массалық ақау: 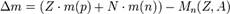 , Ядроның байланыс энергиясы:
, Ядроның байланыс энергиясы: 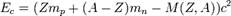 . Ядроның түрленуі кезінде белгілі бір энергия бөлініп шығады.Олай болса атом ядросы түзілгенде н.е ыдырағанда қажетті энергияның бөлінуін ядроның байланыс энергиясы д.а
. Ядроның түрленуі кезінде белгілі бір энергия бөлініп шығады.Олай болса атом ядросы түзілгенде н.е ыдырағанда қажетті энергияның бөлінуін ядроның байланыс энергиясы д.а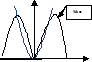 маятник,физикалық маятниктер г.о ның мысалдары бола алады.
маятник,физикалық маятниктер г.о ның мысалдары бола алады.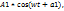 Х2=
Х2= 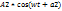 . Екі тербелісті А1 және А2 векторлары арқылы өрнектейік(1 сурет). А векторының ОХ өсіне проекциясы гармоникалық тербелісті береді, екінші жағынан х=х1+х2.Бұдан гармоникалық тербелістерді , векторларды қосу амалымен өрнектеуге болады. Суреттен қорытқы гармоникалық тербелістің амплитудасы
. Екі тербелісті А1 және А2 векторлары арқылы өрнектейік(1 сурет). А векторының ОХ өсіне проекциясы гармоникалық тербелісті береді, екінші жағынан х=х1+х2.Бұдан гармоникалық тербелістерді , векторларды қосу амалымен өрнектеуге болады. Суреттен қорытқы гармоникалық тербелістің амплитудасы 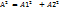 +2*A1*A2cos(a2-a1), фазасы
+2*A1*A2cos(a2-a1), фазасы 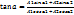 егер фазалар айырмасы а2-а1=±(2m+1)*π (m ріс емес бүтін сан)тең болса қорытқы амплитуда А=A1+A2 шамасына тең, ал егер a2-a1=±2mπ, А=|A1-A2|. Бірінші жағдайда фазалары бірдей де екіншісіне қарама қарсы. Егер ω1≠ωс болса , қорытқы тербеліс амплитудасы толықсымалы гармоникалық тербеліс ретінде қарастыруға болады. Бұндай тербеліс соғу деп ω1=ω ал ω2=ω1+∆ω= ω+∆ω.А1=А2=A, а1=a2=0 деп белгілесек тербеліс теңдеулері Х1=Acosωt, Х2=Acos(ω+∆ω)t, қорытқы тербеліс теңдеуі Х=X1+X2=(2acos∆ωt/2)cosωt шамасына тең. Мұндағы ∆ω- соғудың циклдік жиілігі. Периоды Тс=2π/∆ω =2π/|ω2-ω1|=Т1*Т2/|Т1-Т2|, жиілігі ѵс=1/Tc=|ѵ2-ѵ1|
егер фазалар айырмасы а2-а1=±(2m+1)*π (m ріс емес бүтін сан)тең болса қорытқы амплитуда А=A1+A2 шамасына тең, ал егер a2-a1=±2mπ, А=|A1-A2|. Бірінші жағдайда фазалары бірдей де екіншісіне қарама қарсы. Егер ω1≠ωс болса , қорытқы тербеліс амплитудасы толықсымалы гармоникалық тербеліс ретінде қарастыруға болады. Бұндай тербеліс соғу деп ω1=ω ал ω2=ω1+∆ω= ω+∆ω.А1=А2=A, а1=a2=0 деп белгілесек тербеліс теңдеулері Х1=Acosωt, Х2=Acos(ω+∆ω)t, қорытқы тербеліс теңдеуі Х=X1+X2=(2acos∆ωt/2)cosωt шамасына тең. Мұндағы ∆ω- соғудың циклдік жиілігі. Периоды Тс=2π/∆ω =2π/|ω2-ω1|=Т1*Т2/|Т1-Т2|, жиілігі ѵс=1/Tc=|ѵ2-ѵ1|
 . Ықтималдықты нормалау шарты
. Ықтималдықты нормалау шарты 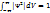 .
. Осы үлестіру Бозе Эйнштейн үлестіру деп аталады. ϻ-Энергияға тәелді емес, бөлшектер санының тығыздығымен және температурамен ғана анықталады химиялық потенциал.
Осы үлестіру Бозе Эйнштейн үлестіру деп аталады. ϻ-Энергияға тәелді емес, бөлшектер санының тығыздығымен және температурамен ғана анықталады химиялық потенциал. (r2
(r2 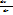 )+
)+  +
+  =
=  =Eᴪ
=Eᴪ .Яғни Бор теориясымен сәйкес болады n бас квант саны,мәні n=1,2…
.Яғни Бор теориясымен сәйкес болады n бас квант саны,мәні n=1,2…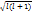
 =ђ
=ђ 


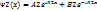

 , K2=
, K2= 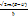
 және
және 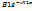 тосқауылға түсетін ,шағылатын де Бройль толқындары.
тосқауылға түсетін ,шағылатын де Бройль толқындары. 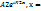 0 шекарасынан сынып өткен толқын, ал
0 шекарасынан сынып өткен толқын, ал 
 тосқауылдан өтіп қайта оралмайтын толқын. Тосқауыл мен бөлшектің айырым энергиясы U~E мен тосқауылдың ені көп болып және бөлшектің массасы ауырлау болса өту ықтималдығы аз болады. Бөлшек энергиясының тосқауыл биіктігінің энергиясынан аздығына қарамастан тосқауылды өту құбылысы тунелдік эффект д.а
тосқауылдан өтіп қайта оралмайтын толқын. Тосқауыл мен бөлшектің айырым энергиясы U~E мен тосқауылдың ені көп болып және бөлшектің массасы ауырлау болса өту ықтималдығы аз болады. Бөлшек энергиясының тосқауыл биіктігінің энергиясынан аздығына қарамастан тосқауылды өту құбылысы тунелдік эффект д.а , T =
, T =  Гармоникалық тербелісте болатын физикалық шамалардың жылдамдағы мен үдеуі формуласы
Гармоникалық тербелісте болатын физикалық шамалардың жылдамдағы мен үдеуі формуласы 
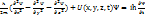 (1)
(1)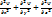 - бөлшектің кеңістіктегі координаты.
- бөлшектің кеңістіктегі координаты.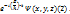 Е – бөлшектің толық энергиясы. Егер (2) өрнекке 1 теңдеудегі функция мәндерін қойып, дифференциалдық теңдеуін аламыз:
Е – бөлшектің толық энергиясы. Егер (2) өрнекке 1 теңдеудегі функция мәндерін қойып, дифференциалдық теңдеуін аламыз: 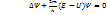 (3) Осы теңдеу Шредингердің бөлшектің стационарлық күйін сипаттайтын теңдеу.
(3) Осы теңдеу Шредингердің бөлшектің стационарлық күйін сипаттайтын теңдеу.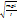 , T=2П
, T=2П 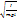 , lкел=
, lкел=  , T=2П
, T=2П 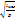
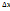 шамасында анықтай аламыз, бірақ дифракция салдарынан импульс алғашқы бағытынан аутқып, саңылауға дейіңгі нақты мәнін жоғалтады. Суреттен
шамасында анықтай аламыз, бірақ дифракция салдарынан импульс алғашқы бағытынан аутқып, саңылауға дейіңгі нақты мәнін жоғалтады. Суреттен 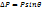 бірінші дифракция максимум шартынан
бірінші дифракция максимум шартынан 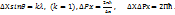 Егер де дифракция суретінің басқа да максимумдерін ескерсек:
Егер де дифракция суретінің басқа да максимумдерін ескерсек: 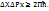
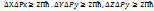 . Сонымен қатар уақыт пен энергияның анықталмаушылық қатыстары да қарастырылады, яғни
. Сонымен қатар уақыт пен энергияның анықталмаушылық қатыстары да қарастырылады, яғни 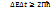 , бұл белгілі жүйфені орташа өмір сүруі уақыты болса, онда оны сипаттайтын энергияны дәл өлшеуге мүмкін емес немесе керісінше.
, бұл белгілі жүйфені орташа өмір сүруі уақыты болса, онда оны сипаттайтын энергияны дәл өлшеуге мүмкін емес немесе керісінше. Маятникті тепе теңдік қалпынан аутқыған кезде шама жағынан mglsin
Маятникті тепе теңдік қалпынан аутқыған кезде шама жағынан mglsin 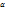 тең айналдырушы күш моменті пайда болады. Мұндағы m – маятниктің массасы, l – жіптің ұзындығы.
тең айналдырушы күш моменті пайда болады. Мұндағы m – маятниктің массасы, l – жіптің ұзындығы.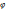
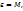 инерция моменті I=ml2 , бұрыштық үдеуін
инерция моменті I=ml2 , бұрыштық үдеуін 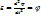 деп белгілесек m
деп белгілесек m 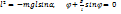 аутқу өтое аз болғандықтан sin
аутқу өтое аз болғандықтан sin 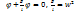 деп белгілесек
деп белгілесек 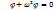 теңдеуі аламыз. Бұл гармоникалық тербелістің теңдеуі. Шешімі
теңдеуі аламыз. Бұл гармоникалық тербелістің теңдеуі. Шешімі 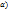 периоды Т=2П
периоды Т=2П 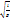
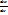 - спектрлік аралықтық бір алқабына келетін дененің бірлік ауданынан шығатын сәуленің қуаты. Энергетикалық жарқырау R=
- спектрлік аралықтық бір алқабына келетін дененің бірлік ауданынан шығатын сәуленің қуаты. Энергетикалық жарқырау R= 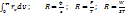
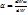 жұтылған энергияның түскен энергияға қатынасы.
жұтылған энергияның түскен энергияға қатынасы.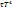 Вин заңы 1) абсолют қара дененің спектрлік сәуле шығарғыштық қабілетінің максимал мәніне келетін жиілік оның температурасына тура пропорционал. Vmax =BT немесе толқын ұзындығы арқылы
Вин заңы 1) абсолют қара дененің спектрлік сәуле шығарғыштық қабілетінің максимал мәніне келетін жиілік оның температурасына тура пропорционал. Vmax =BT немесе толқын ұзындығы арқылы 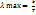
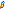 x”+w0x=0 – өшетін тербеліс теңдеуі
x”+w0x=0 – өшетін тербеліс теңдеуі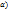
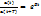 Өшу декременті деп, оның логарифмі өшудің логарифмдік декременті д.а.
Өшу декременті деп, оның логарифмі өшудің логарифмдік декременті д.а.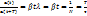
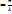 =
= 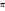 N
N