
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЯВЛЯЕТСЯ ЛИ СОСТОЯНИЕ УСТОЙЧИВЫМ? ⇐ ПредыдущаяСтр 3 из 3 SPH альфа-модель, в отсутствие диссипации, - это консервативная механическая система, выведенная из лагранжиана. Если система находится в покое, например, в однородной камере, то малые возмущения распространяются как звуковые волны. В линейном приближении волны не объединяются, так что энергия, вложенная в моду, остаётся в ней. Если движение становится нелинейным, волны объединяются и энергия распределяется среди мод. Если равновесная статистическая механика имеет силу для этой системы, все моды имели бы одинаковую энергию, а распределение энергии между волновым числом k и k + dk должно быть пропорционально k2 в трех измерениях. Однако известны случаи, например, из проведенного Ферми, Пастом и Уламом (Fermi-Past-Ulam) исследования связанных нелинейных осцилляторов (Ферми и др. 1955; Сегре 1965), что нелинейная недиссипативная система может не эволюционировать до статистического равновесия, но вместо этого перемещает энергию вперед-назад между относительно небольшим количеством мод. В данном случае мы имеем нелинейное взаимодействие по скорости в уравнении движения и по изменению плотности, связанному с изменением скорости. Результаты, представленные Ченом и др. (1999) для альфа-модели континуума показывают, что в пространстве волновых чисел нелинейные члены отклоняют спектр в сторону больших волновых чисел. Получается, что члены скорости в уравнении движения действуют как потенциал, препятствующий накоплению энергии при высоких волновых числах. Это наводит на мысль, что недиссипативная модель передает энергию вперед-назад между высокими и низкими волновыми числами. Важность этого для турбулентности заключается в следующем. Известно, что прямое численное моделирование без диссипации ведет к накоплению энергии в модах высоких волновых чисел. Если диссипация включена в процесс, но она очень слабая при имеющейся разрешающейся способности численного моделирования, то накопление по-прежнему будет иметь место, хотя в конечном итоге, если не происходит подвода энергии, будет затухать. Если имеет место подвод энергии при низких волновых числах, и довольно значительный, то накопление продолжается, так как она прибывает быстрее, чем может выйти. Идея подсеточных моделей состоит в недопущении такого накапливания путем включения дополнительной диссипации. Альфа-модель способна, без диссипации, уменьшать накопление энергии при высоких волновых числах. Чтобы это работало, система должна передавать энергию вперед-назад между высокими и низкими волновыми числами. Как отмечалось ранее, в трехмерной турбулентности перенос осуществляется обоими способами (Piomelli и др. 1991; Jimenez 1995; Pope 2000; Woodward и др. 2001) и, в любое время, одни части области могут переходить на более высокий уровень, а другие – на более низкий уровень. Переход на более низкий уровень – это остаток между двумя гораздо более крупными противоположно направленными потоками. Предварительные исследования одномерной сжимаемой альфа-модели показали, что она имитирует задачу Ферми-Паста-Улама (Fermi-Pasta-Ulam). В частности, когда начальная энергия вносится в основную моду периодической одномерной системы, она движется вперед-назад среди первых пяти мод с пренебрежимо малой энергией, передаваемой другим модам с меньшими волновыми числами. Было проведено 130 расчётов звуковых переходов с 200 частицами, так что использовалось 200 мод и широкая возможность наблюдать перераспределение энергии между модами. Если амплитуда скорости удваивалась, большее число мод (обычно первые 10) распределяло между собой большую часть энергии.  Если энергия вводится в систему, всё ещё остаётся необходимость ввести диссипацию, но она может быть гораздо слабее, чем диссипация, которая применяется в обычных субсеточных моделях. ДИССИПАЦИЯ Предыдущий анализ касался недиссипативной жидкости. Если верно, что недиссипативная SPH модель передает энергию между низкими и высокими волновыми числами для недопущения накопления энергии при высоких волновых числах, то можно добавить небольшое количество диссипации для удаления энергии на шкале разрешающей способности (~h в SPH расчете) таким образом, что с вводом энергии при низких волновых числах система воспроизводит спектр Колмогорова по всем модам, кроме мод с высокими волновыми числами. Член диссипации для SPH основан на
После чего уравнение (4.10) можно записать в виде
Мы можем вывести уравнение для тепловой энергии, потребовав постоянства полной энергии. Используя те же аргументы, что и в Разделе 2.3, но скалярно умножив уравнение для ускорения на
Член, включающий диссипацию, положительно определен, так что SPH диссипация увеличивает тепловую энергию. Легко сделать вывод, что диссипация гарантирует рост энтропии и для каждой частицы. Таким же образом, Е*, квази-энергия, соответствующая рассчитываемым системам, предполагает энтропию каждой частицы постоянной (см. Раздел 2.3) и изменяется во времени согласно уравнению
Так что, как и в случае без усреднения энергии, система эволюционирует к состоянию с минимальной величиной E*. Чтобы установить эти результаты, необходимо было использовать сглаженную скорость СКЕЙЛИНГ И ТУРБУЛЕНТНОСТЬ В предыдущих разделах был изложен формализм SPH-версии альфа-модели турбулентности. В отсутствие диссипации мы возражаем против того, что поток энергии движется вперед-назад между низкими и высокими волновыми числами. Если подвод энергии происходит при низких волновых числах, а система имеет малую диссипацию вышеуказанного типа, то мы полагаем, что SPH – система будет воспроизводить спектр Колмогорова для энергосодержащих мод с низкими волновыми числами. Это предположение поддерживается континуальными расчетами Чена и др. (1999). О некоторых характеристиках данного процесса можно догадываться по скейлинг-аргументам (Колмогоров и Обухов, как описывают Ландау и Лифшиц (1993)), при допущении что (i) детали диссипации несущественны для мод с низкими волновыми числами, а (ii) скорость потерь энергии в различных шкалах длин - постоянна. Мы начинаем с энергии
и полагаем, что имеется определённая скорость потерь энергии от крупномасштабных движений Скорость изменения энергии на единицу массы
тогда как член, включающий Характеристическая скорость -
Если
Таким образом, скорость уменьшается быстрее вместе с l в области сглаживания. Время круговорота задано уравнением
Которое приблизительно постоянно при Если энергия на единицу массы в диапазоне волновых чисел от k до k + dk составляет E(k)dk, тогда E(k) имеет размерность (длина)3/(время)2. Мы можем соотнести это с диссипацией энергии и волновым числом. Для больших шкал длины мы ожидаем, что E(k) будетизменяться как
Для коротких шкал длины мы соотносим E(k) с частью
Затем мы находим
Таким образом, спектр энергий становится более крутым для малых шкал длины. Эти приближённые результаты были подтверждены континуальными расчётами в процессе численных экспериментов (Чен и др. 1999), но подобное широкое исследование требуется для подтверждения этих аргументов для альфа-модели SPH.
ВЫВОДЫ Результаты данной работы можно подытожить следующим образом. (i) Усредненная или сглаженная скорость может быть построена для каждой частицы таким образом, что если каждая частица движется с этой скоростью, импульс и угловой момент не изменяются в сравнении со значениями с несглаженной скоростью. Эта часть нашего анализа такая же, что и для алгоритма XSPH. (ii) Сглаживание скорости согласуется со сглаживанием, которое используется в альфа-модели турбулентности в непрерывном пределе с постоянной плотности. (iii) Лагранжиан частицы может быть построен с использованием в качестве канонических переменных сглаженной скорости (iv) SPH – лагранжиан приводит к уравнениям, которые сохраняют энергию, импульс и угловой момент и удовлетворяют той же теореме дискретной циркуляции Кельвина, что и для SPH без сглаживания скорости. (v) В непрерывном пределе новые SPH - уравнения согласуются с уравнениями альфа-модели турбулентности, когда плотность постоянна. Кроме того, мы предполагаем следующее. (i) Недиссипативный случай предотвращает накопление энергии при самых высоких волновых числах, допускаемых разрешающей способностью, и это происходит путем передачи энергии вперед-назад между низким и высоким волновыми числами. Это предположение поддерживаются скейлинг - аргументами, тем фактом, что это происходит в лабораторной турбулентности, и аналогией с динамическими системами, такими, как задача Ферми-Паста-Улама (Fermi-Past-Ulam). (ii) Слабая диссипация должна быть достаточной для воспроизведения спектра Колмогорова для изотропной однородной турбулентности. Это предположение поддерживается расчетами для непрерывного случая, описанного в работе Чена и др. (1999). (iii) Искусственная вязкость, применяемая в SPH - расчетах, может быть намного меньше, чем вязкость, которая обычно используется в гладких участках течения, при условии, что каждая частица имеет свой собственный коэффициент вязкости. Это предположение поддерживается предварительными расчетами колебаний политропы и ростом неустойчивостей Кельвина-Гельмгольца. Основное внимание в данной работе уделено динамике SPH системы при учёте и без учёта вязкой диссипации. Мы помним о турбулентных процессах, которые развиваются из механических источников, таких как неустойчивости Кельвина-Гельмгольца в струях. Мы не рассматриваем более сложный случай турбулентности, развивающейся в результате тепловых воздействий, как при турбулентной конвекции. В частности, мы не рассматриваем, как сглаживание поля скорости влияет на теплоперенос. Формализм альфа-модели дает нам два поля скоростей и отсюда возникает возможность моделирования повышенной диффузивности, ожидаемой от турбулентности. Как это следует делать, однако, не ясно. Еще один важный вопрос динамики турбулентности – это перемешивание (Warhaft 2000). Эта проблема часто контринтуитивная, с большим числом на первый взгляд ламинарных потоков, ведущих к существенному перемешиванию (Aref и др. 1989). Естественный подход к перемешиванию – лагранжев формализм и, возможно, SPH формулировка предлагает эффективные практические средства определения степени перемешивания как в турбулентном, так и в почти ламинарном потоке. Это другая область исследования, которая открывается теоретическими разработками в данной работе. ОТ АВТОРОВ Частое, приятное, заставляющее думать общение и обмен информацией с Дэррилом Холмом (Darryl Holm) внесли значительный вклад в данную работу. ССЫЛКИ Aref Η., Jones S.W., Mofina S., Zadwadzki I., 1989, Physica D, 37, 423 Bond J., LokT.-S.L„ 1999, Comp. Meth. App. Mech. Eng., 180, 97 Bonet J., 2002, Meshless Methods, Bonn (Conf. 2001). Springer-Verlag, Berlin, in press Bretherton R, 1970, J. Fluid Mech., 44, 19 Chen S., Holm D.D., Margolin L.G., Zhang R., 1999, Physica D, 133,66 Eckart C, 1960, Phys. Fluids, 3,421 Fermi E., Pasta J., Ulam S., 1955, Studies of Non Linear Problems, LA-1940 Feynman R., 1957, Prog. Low Temp. Phys., 1, 17 Gray J., Monaghan JJ., Swift R.P., 2001, Comp. Meth. App. Mech. Eng, 190, 6641 Holm D.D., 1999, Physica D, 133, 215 Jimenez J., 1995, in Verlarde M.G., Christov C.I., eds, FluidPhysics. Lecture Notes on Summer Schools. World Scientific, Singapore Landau L.D., Lifshitz E.M., 1993, Fluid Mechanics, Vol. 6, Course of Theoretical Physics. Pergamon, Oxfords Monaghan J.J., 1989, J. Comput. Phys., 64, 2 Monaghan JJ., 1992, ARA&A, 30, 543 Monaghan J.J., 1994, J. Comput. Phys., 110, 399 Monaghan JJ., 1997, J. Comput. Phys., 136, 298 Monaghan J J., Kos Α., 1999, J. Waterways, Ports, Coastal Ocean Eng., 125, 145 Monaghan J.J., Price D.L., 2001, MNRAS, 328, 381 Morris J.P., Monaghan J.J., 1997, J. Comput. Phys., 136,41 PiomeUi U., Cabot W.H., Moin P., Lee S., 1991, Phys. Fluids A, 3, 1766 Pope S.B., 2000, Turbulent Rows. Cambridge Univ. Press, Cambridge Salmon R., 1988, Ann. Rev. Fluid Mech., 20, 225 Segre E. ed., 1965, Enrico Fermi Collected Papers. Vol. II, Univ. of Chicago Press, Chicago, IL, p. 266 Springel V., Hernquist L., 2002, MNRAS, 333, 649 Warhaft Z., 2000, Ann. Rev. Fluid Mech., 32, 203 Woodward P. et al., 2001, in Ramos E., Cisneros G., eds, Computational Fluid Dynamics, 4th UNAM Supercomputing Conf. World Scientific, Singapore ПРИЛОЖЕНИЕ A: ЧЛЕНЫ Вклад тепловой энергии в лагранжиан дает обычные члены, включающие давление. Члены со скоростью в лагранжиане:
где
Путем замены метки легко показать, что
Используя ранее приведенное выражение для градиента плотности (2.7), после некоторых простых упрощений, первый член в (A.3) можно записать как
где
Второй член в (A.3) более сложный. Сначала рассмотрим вклад
с подобным членом из
Члены ПРИЛОЖЕНИЕ B: УРАВНЕНИЕ КОНТИНУАЛЬНОГО УСКОРЕНИЯ Из (4.9) первым мы рассматриваем член
Для упрощения анализа мы рассматриваем лишь двумерный вариант и полагаем плотность постоянной. Без потери общности, мы рассматриваем лишь Непрерывный предел суммы имеет вид
Разлагая в ряд
где
уравнение (B.2) принимает вид
Комбинируя члены, мы можем записать предыдущее выражение следующим образом
или, при замене
с суммированием по повторяющимся индексам. Остаточный вклад от (4.9) имеет вид
Континуальное выражение для
Выполнив разложение разности скоростей в ряд Тейлора как раньше, получаем приближение
Далее, при постоянной
Этот интеграл обращается в нуль, так как он имеет нечетную симметрию. Остаточный член имеет вид
Умножение (B.12) на —
что, помимо члена давления, дает континуальную форму SPH силы/массы. Существенный член в уравнении Хольма (см.4.22) имеет вид
что можно записать как
Выражение для сглаженной скорости можно обратить и получить ν в виде
если плотность постоянна. При подстановке этого выражения в (B. 15) получаем
Выражение (B.13), континуальный предел члена SPH и (B.17), континуальный член в уравнении Холма, таким образом идентичны.
|
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 175. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (см. 2.27). В данном случае, когда частицы перемещаются со скоростью
(см. 2.27). В данном случае, когда частицы перемещаются со скоростью  , мы заменяем скорость
, мы заменяем скорость  в
в  на
на  , и подставляем этот член в правую часть уравнения (4.10) для получения диссипативных уравнений. Для удобства мы определяем
, и подставляем этот член в правую часть уравнения (4.10) для получения диссипативных уравнений. Для удобства мы определяем
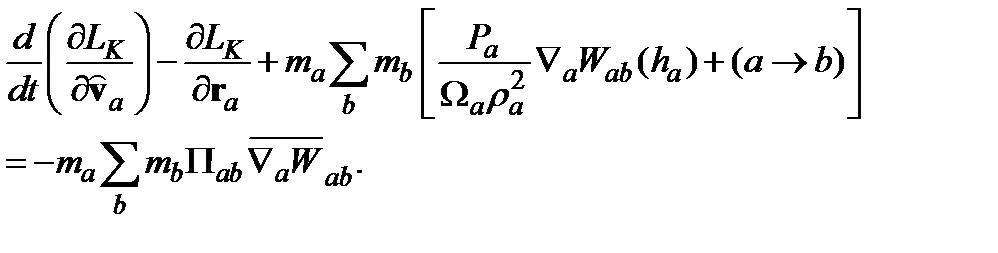 (7.1)
(7.1) получаем уравнение для тепловой энергии частицы:
получаем уравнение для тепловой энергии частицы: (7.2)
(7.2) (7.3)
(7.3) вместо
вместо  в члене вязкости
в члене вязкости 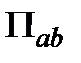 . Таким образом, мы можем ожидать, что SPH - вязкость будет меньше, чем обычно в тех частях течения, где скорость сглажена. В SPH - расчетах член вязкости Π имеет коэффициент (также обозначаемый
. Таким образом, мы можем ожидать, что SPH - вязкость будет меньше, чем обычно в тех частях течения, где скорость сглажена. В SPH - расчетах член вязкости Π имеет коэффициент (также обозначаемый  ),которому может быть присвоено значение ~1. При желании, каждая частица SPH может иметь свою собственную величину
),которому может быть присвоено значение ~1. При желании, каждая частица SPH может иметь свою собственную величину 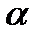 , которую затем можно определить по динамике (Morris и Monaghan 1997) таким образом, что его значение оставляет ~0.1 вдали от ударных волн. Если сглаженная скорость используется в
, которую затем можно определить по динамике (Morris и Monaghan 1997) таким образом, что его значение оставляет ~0.1 вдали от ударных волн. Если сглаженная скорость используется в  , и этот коэффициент изменяется, как описано у Morris и Monaghan (1997), то можно ожидать уменьшения этого коэффициента вдали от ударных волн, и возможно появятся значения ~0.01. Предварительные исследования колебаний политроп и неустойчивостей Кельвина-Гельмгольца показывают, что в этих случаях данное предположение подтверждается. Полное исследование этих эффектов будет представлено в другой работе.
, и этот коэффициент изменяется, как описано у Morris и Monaghan (1997), то можно ожидать уменьшения этого коэффициента вдали от ударных волн, и возможно появятся значения ~0.01. Предварительные исследования колебаний политроп и неустойчивостей Кельвина-Гельмгольца показывают, что в этих случаях данное предположение подтверждается. Полное исследование этих эффектов будет представлено в другой работе. (8.1)
(8.1) , которая ниспадает каскадом через разные шкалы длин до тех пор, пока не будет рассеяна либо слабой SPH вязкостью, либо молекулярной вязкостью.
, которая ниспадает каскадом через разные шкалы длин до тех пор, пока не будет рассеяна либо слабой SPH вязкостью, либо молекулярной вязкостью. , определяемая первым членом в Ε для изменений скорости с изменением характеристической длины l составляет
, определяемая первым членом в Ε для изменений скорости с изменением характеристической длины l составляет (8.2)
(8.2) можно рассчитать из непрерывного предела энергии, который вводит член
можно рассчитать из непрерывного предела энергии, который вводит член  (см. 4.5). Так как a изменяется с изменением длины разрешения, нижеприведенную скейлинг - формулу следует интерпретировать через локальные условия для газа.
(см. 4.5). Так как a изменяется с изменением длины разрешения, нижеприведенную скейлинг - формулу следует интерпретировать через локальные условия для газа. (8.3)
(8.3) , то она сводится к обычному скейлингу скорости Колмогорова
, то она сводится к обычному скейлингу скорости Колмогорова  . Если
. Если  то
то (8.4)
(8.4)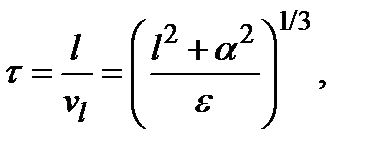 (8.5)
(8.5) . Это указывает на тот факт, что все шкалы длин имеют в принципе одно и то же время круговорота, когда доминирует сглаживание. Эти влияния на шкалу скорости и время круговорота не являются результатом диссипации. Это происходит благодаря членам с квадратом скорости в уравнении для ускорения.
. Это указывает на тот факт, что все шкалы длин имеют в принципе одно и то же время круговорота, когда доминирует сглаживание. Эти влияния на шкалу скорости и время круговорота не являются результатом диссипации. Это происходит благодаря членам с квадратом скорости в уравнении для ускорения. . Затем мы находим
. Затем мы находим (8.6)
(8.6) , котораязависит от характеристической скорости и шкал длины. Учёт (8.5) дает
, котораязависит от характеристической скорости и шкал длины. Учёт (8.5) дает (8.7)
(8.7)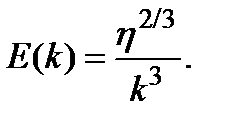 (8.8)
(8.8) и
и 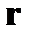 . Эта лагранжиан частица имеет такую же структуру, что и непрерывный лагранжиан в альфа-модели.
. Эта лагранжиан частица имеет такую же структуру, что и непрерывный лагранжиан в альфа-модели.
 (A.1)
(A.1) (A.2)
(A.2) можно заменить на
можно заменить на  в (A. 1). Тогда
в (A. 1). Тогда (A.3)
(A.3) (A.4)
(A.4) (A.5)
(A.5)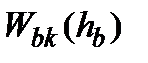 в
в  . Находим
. Находим (A.6)
(A.6)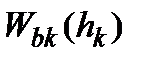 в
в  имеет вид
имеет вид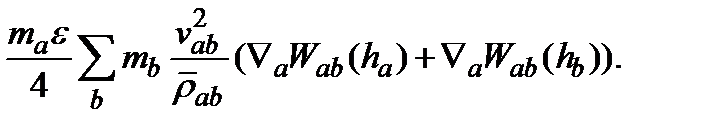 (A.7)
(A.7) дают члены, включающие H' в (4.9).
дают члены, включающие H' в (4.9). (B.1)
(B.1) компонент.
компонент. (B.2)
(B.2) относительно
относительно  до второго порядка, и сохраняя только члены нечётного порядка по
до второго порядка, и сохраняя только члены нечётного порядка по  и чётного порядка по
и чётного порядка по 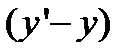 , (B.2) приведём к виду
, (B.2) приведём к виду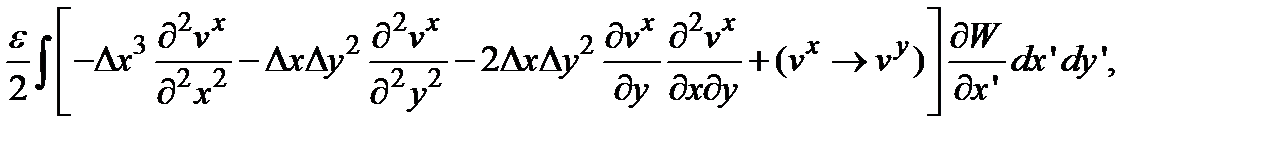 (B.3)
(B.3) и
и  означают
означают  и
и  компоненты
компоненты 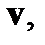 а
а  и
и  означают
означают  включает ряд членов, идентичных предыдущим, но с заменой
включает ряд членов, идентичных предыдущим, но с заменой  (B.4)
(B.4) (B.5)
(B.5) (B.6)
(B.6) и
и  на
на  и
и  , соответственно,
, соответственно, (B.7)
(B.7) (B.8)
(B.8) имеет вид
имеет вид (B.9)
(B.9) (B.10)
(B.10)
 (B.11)
(B.11) (B.12)
(B.12) в комбинации с (12.7) дает
в комбинации с (12.7) дает (B.13)
(B.13) (B.14)
(B.14) (B.15)
(B.15) (B.16)
(B.16)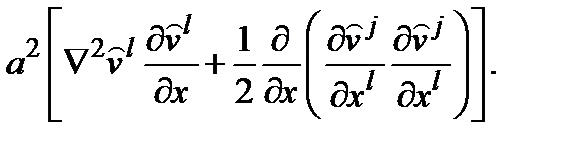 (B.17)
(B.17)