
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Комментарии к тепловой энергииСтр 1 из 3Следующая ⇒ SPH compressible turbulence J. J. Monaghan School of Mathematics Sciences, Monash University, Clayton 3800, Australia Accepted 2002 May 9. Received 2002 May 6; in original form 2002 February 5 SPH-версия турбулентности потока сжимаемой жидкости J. J. Monaghan* Школа математических наук, университет Монаш, Клейтон 3800, Австралия Принято 9 мая 2002 г. Получено 6 мая 2002 г.; в исходном виде 5 февраля 2002 г. РЕФЕРАТ В данной работе сформулирован метод гидродинамики сглаженных частиц (SPH) альфа-модели турбулентности, разработанной Холмом (Holm) и его коллегами, для потока сжимаемой жидкости с решением, изменяемым в пространстве и времени. Альфа-модель включает в себя два поля скоростей. Одно поле скоростей получают из уравнения импульса движения, другое – путем усреднения этого поля скоростей, как в версии метода SPH, называемой XSPH. Частицы (элементы жидкости) движутся с усредненной скоростью. По аналогии с альфа-моделью континуума, мы получаем лагранжиан частицы, из чего можно вывести альфа-уравнения SPH. Система удовлетворяет условиям теоремы дискретной циркуляции Кельвина, идентичной полученной без усреднения скорости. Кроме того, сохраняются энергия, импульс и угловой момент. Мы показываем, что континуумный эквивалент уравнений SPH идентичен альфа-модели континуума, и мы предполагаем, что их модель континуума будет иметь такие же желательные характеристики, включая гашение энергии в модах высоких волновых чисел, даже при нулевом рассеивании. Независимо от вопросов, касающихся моделирования турбулентности, SPH альфа-модель – это значительное расширение алгоритма XSPH, которое уменьшает неупорядоченность в масштабах коротких длин волн и сохраняет интегралы движения. SPH альфа-модель проста в реализации.  Ключевые слова:гидродинамика - турбулентность. ВВЕДЕНИЕ Во многих моделях гидродинамики сглаженных частиц (SPH), рассчитывающих астрофизические течения, возникают области, где SPH частицы проходят друг через друга. При моделировании континуума это перетекание нефизическое, так как оно подразумевает, что поле скоростей локально многозначное. Проблему можно решить путем ввода достаточной вязкости, но при этом возникают нежелательные побочные эффекты, например, избыточный спад сдвигового напряжения. По этой причине была разработана версия SPH, называемая XSPH (Monaghan 1989, 1992). Идея проста. Каждая частица движется со сглаженной скоростью, которая создается путем усреднения скоростей соседних частиц. Таким образом, исключается или значительно уменьшается встречный поток. Эта процедура недиссипативная и сохраняет импульс и угловой момент. Сглаживание имеет еще одно преимущество – уменьшение локальной неупорядоченности. Его недостаток заключается в том, что энергия не сохраняется. Способ сохранения энергии, и в то же время более широкого применения SPH предлагает альфа-модель турбулентности (см. ссылки Holm 1999). Это минималистская модель турбулентности, которая учитывает ограниченную разрешающую способность любого численного моделирования или экспериментального измерения, путем использования средней скорости движения жидкости, и в то же время сохранения инвариантов потока. Это достигается путем вывода уравнений движения из уравнения Лагранжа, что автоматически дает члены напряжения, которые предполагаются в других моделях турбулентности (обсуждение этих моделей представлено в работе Поупа (Pope) в 2000). В альфа-уравнениях сохраняется циркуляция жидкости (в случае когда она является инвариантом исходных уравнений), а также аддитивные интегралы энергии и импульса. Кроме того, численное моделирование (Чен и др. 1999) показывает, что альфа-модель континуума воспроизводит спектр Колмогорова для трёхмерной турбулентности. Особенность альфа-модели континуума заключается в том, что присутствие членов градиента скорости в силе значительно снижает вклад энергии в моды с высокими волновыми числами. В SPH версии воздействие на частицу содержит нелинейные члены, которые зависят от скоростей соседних частиц. Мы полагаем, что эти члены обеспечивают передачу энергии «вперёд-назад» от малых и больших волновых чисел. В качестве примера приведем задачу Ферми-Паста-Улама (Fermi, Pasta & Ulam 1955; Серже (Segre) 1965), где члены нелинейно изменяющейся силы не приводят к статистическому равновесию (что означало бы присутствие большей части энергии на высоких волновых числах), а к перетеканию энергии «вперед-назад» между небольшим количеством мод с низким волновым числом. Подобное течение вперед-назад встречается при трехмерной турбулентности (Piomelli и др. 1991; Jimenez 1995 ; Pope 2000; Woodward и др. 2001), хотя это часто неясно при описании результирующего потока, который движется от низких к высоким волновым числам. Фактически в любое время в разных частях турбулентной системы поток энергии может двигаться либо вверх, либо вниз по шкале волновых чисел. Преимущество альфа-модели состоит в том, что если недиссипативная система уже гасит энергию в модах высоких волновых чисел, то можно ввести слабую диссипацию для выполнения этой задачи смещения энергии. Другие модели турбулентности пытаются сделать это, используя стандартную форму уравнений Навье-Стокса с диссипацией, достаточно сильной для снятия энергии при высоких волновых числах. В данной работе мы выводим SPH - альфа-уравнения из лагранжиана для частиц, используя в качестве наводящего уравнение неразрывности. Мы показываем, что система сохраняет дискретную форму теоремы циркуляции Кельвина в дополнение к аддитивным интегралам энергии и момента. Эти уравнения вводятся достаточно просто, а дополнительные расчетные затраты пренебрежимо малы. Так как эта модель турбулентности требует лишь минимальной диссипации, то должна иметься возможность существенного уменьшения стандартной SPH вязкости на участках потока, расположенных вдали от ударных волн. Объединив эту идею с идеей изменения коэффициента вязкости для каждой частицы в отдельности (Morris и Monaghan 1997), вязкость можно было бы уменьшить в ~100 раз вдали от ударных волн. План данной работы следующий. Мы выводим стандартную систему уравнений для SPH из Лагранжиана с масштабом разрешения, согласующимся с плотностью. Уравнение импульса принимает такую же форму, что и уравнение, полученное Springel и Hernquist (2002) с использованием множителей Лагранжа для ограничения длины отрезка сглаживания. Однако полученное уравнение для тепловой энергии отличается от обычных уравнений тепловой энергии. Мы показываем, что уравнения движения приводят к теореме дискретной циркуляции Кельвина в дополнение к аддитивным интегралам энергии и импульса. Затем мы определяем усреднение скорости согласно XSPH и показываем, что оно согласуется с альфа-моделью континуума. Руководствуясь альфа-моделью, мы предлагаем дискретную SPH-форму Лагранжиана. Уравнения движения Лагранжа согласуются в континуальном пределе с уравнениями альфа-модели. Сохранение циркуляции принимает в точности такую же форму, как и в случае, когда скорости не усреднены. И, наконец, мы обсуждаем диссипацию и скейлинг, показывая, что энергетический спектр обрывается быстрее, чем спектр Колмогорова на масштабах коротких длин волн. Большая вычислительная работа, необходимая для подтверждения этих гипотез и скейлинга, будет представлен в другом месте. УРАВНЕНИЯ СРАВНЕНИЯ Уравнение для импульса В данном разделе мы выводим стандартную систему SPH уравнений без усреднения скорости, для сравнения с уравнениями альфа-модели. Стандартная система SPH уравнений будет получена для Лагранжиана, вполне допускающее изменение длины разрешения h с изменением плотности. Данные уравнения подобны уравнениям, представленным в работе Springel и Hernquist (2002), а также Bonet (Bonet и Lok 1999; Bonet 2002) Однако данное уравнение энергии отличается от уравнений, которые рассматриваются в работе Springel и Hernquist (2002). Формулировку можно легко распространить и на релятивистский случай, используя анализ Monaghan и Price (2001). Лагранжиан для сжимаемого недиссипативного течения имеет вид (Eckart 1960):
В SPH виде плотность частицы a можно записать как
где A и Β - константы. Более того, тогда как обычно оценивают Уравнения движения следуют из вариации действия с сохранением энтропии. Из уравнений Лагранжа для частицы a
Из (2.4) получаем
где
Ω = 1 + О(h2). Первый закон термодинамики, когда энтропия постоянна, дает
где Ρ - давление. Уравнение для ускорения (2.6) с учётом (2.7) и (2.9) принимает следующий вид
Законы сохранения Симметрия Лагранжиана приводит непосредственно к законам сохранения. В частности, плотность (а, следовательно, и Ρ когда s постоянна) и гравитационный потенциал не зависят от переносов и поворотов системы координат. Соответственно сохраняются импульс и угловой момент. Если система вязкая, тогда член с вязкостью можно построить так, чтобы импульс и угловой момент по-прежнему сохранялись (см. раздел 2.3). В случае постоянной энтропии сохранение энергии можно показать непосредственно, заметив что
Если энтропия остается постоянной во время движения, система частиц инвариантна относительно других преобразований. Рассмотрим, например, группу частиц с одинаковой массой и энтропией, размеченных в виде ожерелья. Представим каждую частицу в петле, смещая ее в положение соседней частицы (вокруг ожерелья) и придавая ей скорость соседней частицы. Так как энтропия постоянна, ничего не меняется, и формула Лагранжа, таким образом, инвариантна относительно данного преобразования. Обсуждение получающейся инвариантной величины представлено в работе Monaghan и Price (2001). Мы повторяем здесь ключевые элементы аргументации, так как намерены показать (см. Раздел 6), что, несмотря на движение жидкости со сглаженным полем скорости, сохряняется тот же инвариант. Изменение L можно аппроксимировать выражением
где j – метка частицы на петле. Так как система инвариантна относительно данного преобразования, мы принимаем δL = 0. Изменение положения и скорости дается уравнениями
и
Используя уравнения Лагранжа мы можем переписать (2.12) в виде Вспоминая, что массы частиц предполагаются равными, делаем вывод, что
так что величина
сохраняется в этом приближении для каждой петли. Сохранение лишь приблизительное, так как изменение Лагранжиана носит дискретный характер, и аппроксимируется с точностью только до членов первого порядка. Однако, если частицы расположены достаточно близко друг к другу, (2.17) аппроксимирует теорему циркуляции с произвольной точностью. Близкие аргументы были использованы Фейнманом (Feynman) (1957) для установления из инвариантности волновой функции того факта, что циркуляцию следует квантовать. Система также инвариантна относительно частиц, смещающихся вокруг петли в противоположном направлении. Это дает аппроксимацию циркуляции с противоположным знаком. При их объединении (с учетом их знаков, так чтобы вычесть один из другого) мы получаем
что является лучшим приближением для циркуляции сплошной среды. Погрешности дискретного приближения к теореме циркуляции возникают из-за членов более высокого порядка малости при вариации функции Лагранжа. Эти погрешности становятся менее значительными, по мере того как пространственный масштаб изменения поля скорости становится больше, чем для разделения частиц. Если скорость постоянна, то
как и ожидалось. Если скорость является результатом твердотельного вращения с угловой скоростью Ω, то
Взяв для удобства начало системы координат внутри петли, площадь треугольника, который образуют
где A – площадь внутри петли частиц. Завихрённость составляет 2Ω и (4.18) дает такой же результат, как при применении теоремы Стокса (Stokes) к интегралу циркуляции. Еще несколько примеров приводят Monaghan и Price (2001). Salmon (1988), следом за Bretherton (1970) также установил закон циркуляции, обращаясь к инвариантности перестановки частиц. Но его анализ основан на уравнениях сплошной среды, поэтому он более сложный, чем наш.
Комментарии к тепловой энергии Если энтропия постоянна, мы можем получить скорость изменения тепловой энергии из скорости изменения плотности. Скорость изменения плотности получаем путем дифференцирования (2.4) по времени, с учетом того факта, что hа – это функция
где
что не согласуется со всеми уравнениями тепловой энергии, предложенными Springel и Hemquist (2002). Наше уравнение тепловой энергии также можно вывести, сначала составив векторное произведение
где ЕK – кинетическая энергия, а ЕG – гравитационная энергия. Если метки a и b поменять местами в части двойного суммирования с включением Pb , мы можем записать (2.24) как
Сохранение полной энергии требует, чтобы правая часть выражения (2.25) была равна
откуда следует (2.23). В расчеты SPH включаем вязкую диссипацию путем добавления
к члену давления Monaghan (1997). Величина σаb – это положительно определенный параметр, инвариантный относительно перестановки a и b. Он родственен физическому коэффициенту вязкости или искусственному коэффициенту вязкости, зависящему от скорости звука [см. Monaghan (1997) для конкретного вида, представленного в (2.27), и Monaghan (1992) для альтернативного варианта Πab]. Соответственно, мы добавляем член
в правую часть уравнения (2.10), где
Импульс и угловой момент по-прежнему сохраняются, так как сила вязкости проходит вдоль линии, соединяющей центры SPH- частиц. Следуя схеме вывода, приведшего к (2.26), находим
Мы можем записать Существует еще один подход к введению диссипации, аналогичный подходу, который используется при моделировании жидкостей при нормальных температурах и давлениях. В этих случаях изменением энтропии обычно пренебрегают, а доминирующий эффект заключается к сведению кинетической энергии до нуля. Это случай для воды, изначально плещущейся в лабораторной емкости. В этом случае мы записываем (2.24), с добавлением диссипативного члена, в виде
где только члены давления включены в скорость изменения тепловой энергии. Так как правая часть уравнения (2.31) отрицательна, уравнения SPH гарантируют, что диссипация будет вызывать уменьшение E*, как и должно быть. Например, осциллирующая политропа, смоделированная при постоянной энтропии всех частиц, будет эволюционировать до состояния, при котором E* минимально. Когда она достигает этого состояния, Еκ становится равной нулю. УСРЕДНЕНИЕ ПОЛЯ СКОРОСТЕЙ В стандартных SPH расчетах положение частицы a определяется путем интегрирования
Однако частицы могут перетекать друг через друга, если только вязкость невелика. По этой причине была предложена версия XSPH для SPH (Monaghan 1989), где частицы двигались со сглаженной скоростью, но уравнение для ускорения оставалось неизменным. Сглаженная скорость
Численные эксперименты показывают, что значение
но можно использовать и другие симметричные средние. В данной работе мы используем (3.3), так как данное выражение позволяет некоторым образом упростить алгебру в уравнениях Лагранжа. Κ(α, b) – это ядро сглаживания, которое может отличаться от ядра, применяемого в других уравнениях SPH. В данной работе мы полагаем, что ядро имеет симметричную форму
Обеспечивая соответствующую симметрию для членов уравнения (3.2), мы гарантируем, что ситема сохраняет линейный и угловой моменты. Подробная информация представлена в Разделе 5. SPH частицы движутся согласно уравнению
В непрерывном пределе уравнение (3.2) принимает вид
где
Разложение в ряд Тейлора p(r'), v(r') и h(p(r')) относительно
где
Определяет значение
как в альфа-модели континуума. Для типичных SPH ядер |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 174. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 где u (p, s) – тепловая энергия на единицу массы, являющаяся функцией плотности ρ и энтропии s. SPH форма Лагранжиана (2.1) с учётом самогравитации имеет вид
где u (p, s) – тепловая энергия на единицу массы, являющаяся функцией плотности ρ и энтропии s. SPH форма Лагранжиана (2.1) с учётом самогравитации имеет вид где
где В этих уравнениях mb - масса, vb - скорость, rb - координаты, sb – энтропия, и
В этих уравнениях mb - масса, vb - скорость, rb - координаты, sb – энтропия, и  – плотность SPH частицы b. На практике гравитационный член сглаживают для удаления сингулярности, при rb =rk.
– плотность SPH частицы b. На практике гравитационный член сглаживают для удаления сингулярности, при rb =rk. Во многих моделях SPH ha выбирают таким образом, чтобы частица a имела определенное количество соседей. Однако, чтобы остаться в рамках Лагранжевого формализма, следует считать h как функцию координат, и проще всего это сделать, предположив что ha является функцией
Во многих моделях SPH ha выбирают таким образом, чтобы частица a имела определенное количество соседей. Однако, чтобы остаться в рамках Лагранжевого формализма, следует считать h как функцию координат, и проще всего это сделать, предположив что ha является функцией 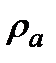 , которую мы обозначим H(
, которую мы обозначим H(  где d - размерность, но может быть использована и более общая функция. Например, во избежание произвольно большого h, при котором ρ становится очень малым, можно выбрать
где d - размерность, но может быть использована и более общая функция. Например, во избежание произвольно большого h, при котором ρ становится очень малым, можно выбрать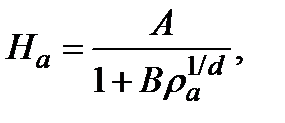
 как функции координат. Уравнение (2.4) – это нелинейная функция для
как функции координат. Уравнение (2.4) – это нелинейная функция для  находим
находим

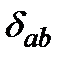 – дельта-функция Кронекера,
– дельта-функция Кронекера,  - градиент W, взятый по координатам частицы a, припостоянном h (мы используем это условное обозначение во всей статье), и
- градиент W, взятый по координатам частицы a, припостоянном h (мы используем это условное обозначение во всей статье), и где
где  означает
означает  . При гладком изменении плотности получим
. При гладком изменении плотности получим
 Уравнение движения (2.10) в точности такое же, как и уравнение движения, полученное Springel и Hernquist (2002), которые ввели ограничения на h с множителем Лагранжа. Если жидкость находится в контейнере, то контейнер может быть представлен граничными силами (Monaghan 1994; Monaghan & Kos 1999).
Уравнение движения (2.10) в точности такое же, как и уравнение движения, полученное Springel и Hernquist (2002), которые ввели ограничения на h с множителем Лагранжа. Если жидкость находится в контейнере, то контейнер может быть представлен граничными силами (Monaghan 1994; Monaghan & Kos 1999).
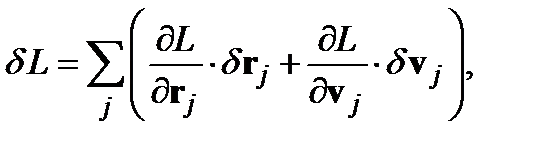 (2.12)
(2.12) (2.13)
(2.13)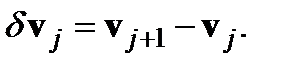 (2.14)
(2.14) (2.15)
(2.15) (2.16)
(2.16) (2.17)
(2.17) (2.18)
(2.18)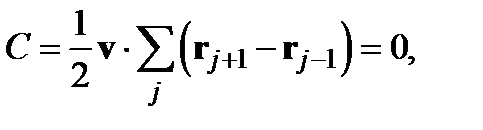 (2.19)
(2.19) (2.20)
(2.20)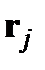 и
и  составляет
составляет  Площадь рассчитывается дважды, как если бы петля лежала на плоскости с нормалью
Площадь рассчитывается дважды, как если бы петля лежала на плоскости с нормалью 
 (2.21)
(2.21) (2.22)
(2.22)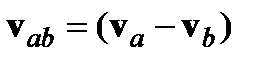 . Скорость изменения тепловой энергии при постоянной энтропии определяется уравнением
. Скорость изменения тепловой энергии при постоянной энтропии определяется уравнением (2.23)
(2.23) и (2.10), а затем выполнив суммирование по a. Мы получаем
и (2.10), а затем выполнив суммирование по a. Мы получаем (2.24)
(2.24)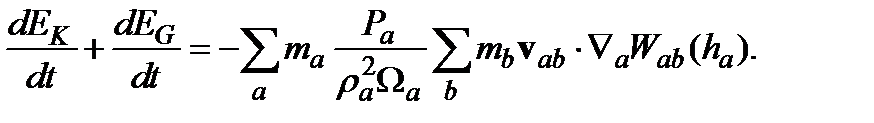 (2.25)
(2.25) . Таким образом,
. Таким образом, (2.26)
(2.26) (2.27)
(2.27) (2.28)
(2.28) (2.29)
(2.29) (2.30)
(2.30) в виде
в виде  , где
, где  . Отсюда следует, что вклад вязкости в du/dt неотрицателен. Также легко показать, что когда жидкость вязкая, изменение энтропии также неотрицательно.
. Отсюда следует, что вклад вязкости в du/dt неотрицателен. Также легко показать, что когда жидкость вязкая, изменение энтропии также неотрицательно. (2.31)
(2.31) (3.1)
(3.1) определяется усреднением по скоростям соседних частиц в соответствии с соотношением
определяется усреднением по скоростям соседних частиц в соответствии с соотношением (3.2)
(3.2)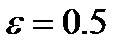 эффективно при сглаживании локальных колебаний скорости, а
эффективно при сглаживании локальных колебаний скорости, а  может привести к неустойчивости (это подтверждается исследованиями дисперсного соотношения для волн в упругих материалах (Gray, Monaghan и Swift 2001).
может привести к неустойчивости (это подтверждается исследованиями дисперсного соотношения для волн в упругих материалах (Gray, Monaghan и Swift 2001).  означает среднюю плотность, симметричную относительно a и b, например
означает среднюю плотность, симметричную относительно a и b, например (3.3)
(3.3) (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) показывающее, что при интегрировании симметрия ядра означает обращение в нуль членов с нечетной симметрией в компонентах
показывающее, что при интегрировании симметрия ядра означает обращение в нуль членов с нечетной симметрией в компонентах  дает приближение
дает приближение (3.8)
(3.8) (3.9)
(3.9) в альфа-модели, хотя, в нашем анализе,
в альфа-модели, хотя, в нашем анализе, 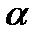 может различаться для каждой частицы и, поскольку
может различаться для каждой частицы и, поскольку  может изменяться во времени, также может изменяться, и
может изменяться во времени, также может изменяться, и 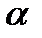 . Если ρ – постоянна, уравнение (3.8) сводится к следующему
. Если ρ – постоянна, уравнение (3.8) сводится к следующему (3.10)
(3.10) Соответственно, при условии, что масштаб изменения поля скоростей гораздо больше, чем h, приближение (3.8) будет удовлетворительным. Однако наше исходное XSPH сглаживание (3.2) применяется независимо от масштаба изменения поля скоростей. В частности, мы ожидаем, что оно может использоваться даже при наличии ударных волн .
Соответственно, при условии, что масштаб изменения поля скоростей гораздо больше, чем h, приближение (3.8) будет удовлетворительным. Однако наше исходное XSPH сглаживание (3.2) применяется независимо от масштаба изменения поля скоростей. В частности, мы ожидаем, что оно может использоваться даже при наличии ударных волн .