
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ XSPH - МЕТОДАВ анализе Хольма (Holm) (1999) предлагается следующий вид лагранжиана
где канонические координаты для частицы b - это Часть с кинетической энергией данного лагранжиана можно перезаписать, обращая (3.2), что дает
где погрешности обращения - порядка Ο (h4). Затем мы получаем уравнение
которое является положительно определенным. Если суммы по k аппроксимированы интегралами, и мы полагаем плотность постоянной, разложение в ряд Тейлора разности скоростей в подынтегральном выражении, с последующим интегрированием, показывает что
где
В отсутствие диссипации и внешних сил эта величина инвариантна для несжимаемой жидкости (Holm 1999). Она положительно определена, квадратична по скоростям, и заменяет собой обычную кинетическую энергию. Отметим, в частности, члены  Уравнения Лагранжа имеют вид:
Первая величина, которая нам нужна, это канонический импульс для частицы a
которая приводится к
так что канонический импульс уравнения Лагранжа, определенный с Оставшийся член, необходимый для уравнения движения частицы a - это
где (a → b) обозначает члены, идентичные предыдущим, но a и b взаимозаменяемы за исключением в
и
Уравнения, необходимые для SPH альфа-модели – это уравнение для ускорения (4.10), и уравнение для плотности, либо в форме суммирования (2.4), либо в форме уравнения непрерывности (2.22):
вместе с соотношением
Эти замечательно простые уравнения составляют SPH альфа-модель. Они включают в себя все желательные свойства уравнений Holm (1999) для несжимаемой жидкости, обобщенные на сжимаемые течения. Если среда является самогравитирующей, то можно добавить члены, ответственные за гравитацию, как в Разделе 2. Эти новые уравнения отличаются от уравнений Раздела 2, например (2.10), так как усреднение скорости приводит к членам, в выражении для силы, зависимым от скорости, и частицы движутся со сглаженной скоростью. В остальном уравнения очень похожи. Чтобы сравнить наши результаты с результатами для несжимаемой альфа-модели, примем, что h и ρ постоянны. В этом случае Ω = 1, а член, включающий ν, исчезает, так как величина
Если суммы в уравнениях SPH преобразованы в интегралы, доминирующие члены дают континуальную альфа-модель (подробности см. в Приложении B). В частности, мы снова получаем уравнение Хольма для ускорения (Holm 1999, уравнение 143)
Таким образом, мы достигли нашей цели создания модели турбулентности, основанной на лагранжиане, которая сводится к альфа-модели в континуальном пределе. В последующих разделах мы исследуем некоторые свойства SPH-модели. ЗАКОНЫ СОХРАНЕНИЯ В отсутствие границ и внешних сил лагранжиан L инвариантен относительно переносов и поворотов. Из-за инвариантности относительно переноса δr системы координат, изменение δL в L должно быть нулевым. Таким образом,
Из уравнения Лагранжа мы можем подставить производную от L, получим:
так что линейный импульс,
сохраняется. Если система координат поворачивается на
Производя замены
Так как
сохраняется. Так как лагранжиан не имеет явной зависимости от времени, то существует инвариант
который уместно назвать энергией. Используя (4.3) мы можем записать
Если энтропия постоянна, то система также инвариантна относительно преобразования ожерелья, рассмотренного ранее (Раздел 2.2). В данном случае частицы, имеющие предположительно одну и ту же массу и энтропию, сдвигаются в соседнее положение на петле и дают Изменение L можно записать следующим образом
где j обозначает метку частицы на петле. Изменение положения и скорости задается равенствами
и
Используя уравнения Лагранжа, мы можем переписать (5.4) в следующем виде
и с учетом равенства масс частиц, вывести формулу
которая тождественна теореме о дискретной циркуляции (2.16). Читатель отметит, что этот результат зависит от того факта, что канонический импульс частицы j – это Результаты данного раздела показывают, что SPH альфа-модель сохраняет импульс, угловой момент и циркуляцию идентичные по форме для стандартной SPH модели без средних скоростей. Соответственно, если мы измеряем эти сохраняемые величины в начальное время, они будут оставаться постоянными, несмотря на то, что уравнения движения теперь содержат новые, зависимые от скорости члены, а частицы движутся со средней скоростью. |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 153. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (4.1)
(4.1)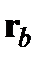 , её скорость -
, её скорость -  . Для простоты мы не включили гравитационные силы. Их можно легко ввести в конечные уравнения.
. Для простоты мы не включили гравитационные силы. Их можно легко ввести в конечные уравнения. (4.2)
(4.2) (4.3)
(4.3) (4.4)
(4.4)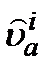 обозначает i-компоненту
обозначает i-компоненту  , и производится суммирование по i. Подстановка этого результата в (4.3) дает
, и производится суммирование по i. Подстановка этого результата в (4.3) дает (4.5)
(4.5) которые играют ключевую роль в распределении энергии. Эквивалент SPH – это сумма (4.3), включающая квадрат разности скоростей. Эта сумма включает в себя только соседние частицы, и является малой, если они имеют близкие скорости. Она становится большой только когда скорости соседних частиц различаются по знаку или величине или то и другое одновременно. Это происходит когда имеет место значительное изменение ν на шкале h. Такое изменение эквивалентно существованию мод с высокими волновыми числами.
которые играют ключевую роль в распределении энергии. Эквивалент SPH – это сумма (4.3), включающая квадрат разности скоростей. Эта сумма включает в себя только соседние частицы, и является малой, если они имеют близкие скорости. Она становится большой только когда скорости соседних частиц различаются по знаку или величине или то и другое одновременно. Это происходит когда имеет место значительное изменение ν на шкале h. Такое изменение эквивалентно существованию мод с высокими волновыми числами. (4.6)
(4.6) (4.7)
(4.7) (4.8)- (4.9)
(4.8)- (4.9) – это нормальный импульс, построенный с
– это нормальный импульс, построенный с  . Это двойственное отношение между
. Это двойственное отношение между 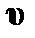 и
и 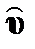 напоминает нам о связи между скоростями Эйлера и Лагранжа, о которых упоминает Holm (1999).
напоминает нам о связи между скоростями Эйлера и Лагранжа, о которых упоминает Holm (1999). . Подробности этого расчета представлены в Приложении A. Подстановка в (4.6) дает
. Подробности этого расчета представлены в Приложении A. Подстановка в (4.6) дает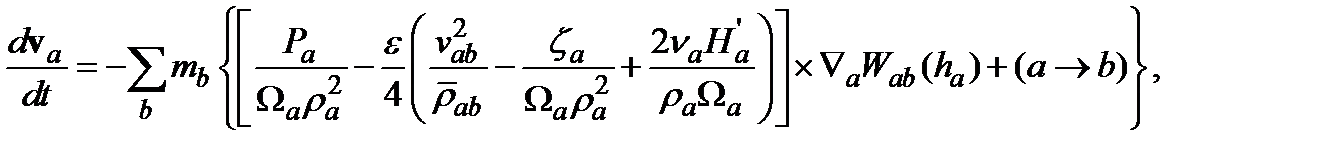 (4.10)
(4.10)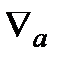 , а другие величины, которые не определены ранее, имеют следующие значения:
, а другие величины, которые не определены ранее, имеют следующие значения: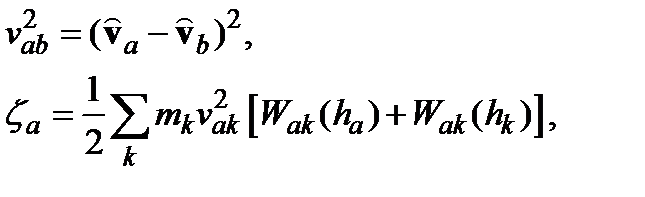

 (4.11)
(4.11)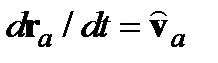 . Субстанциональная производная определяется равенством
. Субстанциональная производная определяется равенством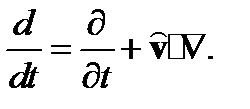 (4.12)
(4.12) равна нулю. Уравнение движения принимает вид
равна нулю. Уравнение движения принимает вид (4.13)
(4.13) (4.14)
(4.14) (5.1)
(5.1) (5.2)
(5.2) (5.3)
(5.3) , то
, то  есть
есть 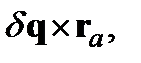 и
и  -
-  . Так как L инвариантна, то
. Так как L инвариантна, то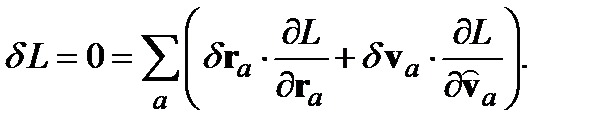 (5.4)
(5.4) и используя уравнения Лагранжа в (5.4), находим
и используя уравнения Лагранжа в (5.4), находим (5.5)
(5.5) (5.6)
(5.6) (5.7)-(5.8)
(5.7)-(5.8) (5.9)
(5.9) новое положение.
новое положение. (5.10)
(5.10)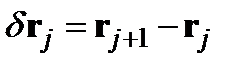 (5.11)
(5.11) (5.12)
(5.12) (5.13)
(5.13) (5.14)
(5.14) .
.