
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Исследование формы гиперболыГипербола лежит за полосой со сторонами x = ± a. Действительно, согласно уравнению гиперболы имеет место неравенство x2/a2≥1→x2≥a2→|x|≥a Гипербола является симметричной относительно начала координат и относительно координатных осей.Гипербола имеет две асимптоты у =±b/a*x к которым приближаются точки гиперболы при удалении их от начала координат. y2/b2 =x2/a2 = -1 Предел расстояния между точками асимптоты и точками гиперболы равен
График гиперболы
21. Параболой называется геометрическое место точек на плоскости, расстояния которых до некоторой точки, называемой фокусом и до некоторой прямой, называемой директрисой, не проходящей через фокус, равны. Через d – расстояние от точки до директрисы, а через р расстояние от фокуса до директрисы. Величину называют параметром параболы, его геометрический смысл раскрыт далее. Точка М будет лежать на данной параболе в том и только в том случае, когда r = d.
Далее избавимся от иррациональности
Уравнение y2 = 2 p x называется каноническим уравнением параболы. 
и, учитывая, что x ≥ 0, получаем
т.е. величины r и d равны, что и требовалось показать. Таким образом, уравнению y2 = 2 p x удовлетворяют координаты точек данной параболы, и только они. Исследование формы параболы
Точка О называется вершиной параболы, ось симметрии (ось Ох) — осью параболы. 22. Параметрические уравнения плоскости В векторном виде В координатах Если прямая параллельна плоскости, то точка Таким образом, условие параллельности прямой и плоскости записывается следующей системой: Для параллельности прямой a, не лежащей в плоскости
23. Уравнение плоскости, проходящей через три различные точки
Если известны три различные точки, не лежащие на одной прямой, то легко найти два неколлинеарных вектора, параллельных данной плоскости:
24. Нормальное уравнение плоскости вида cos a *x + cos b * y + cos y * z – p = 0 задает в прямоугольной системе координат Oxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости Нормальное уравнение плоскости представляет собой общее уравнение плоскости вида Ax + By + Cz + D = 0, в котором числа A, B и C таковы, что длина нормального вектора плоскости Расстояние от точки до плоскости равно абсолютной величине числа, которое получается при подстановке координат точки в левую часть нормального уравнения плоскости. Формула:
25. Если две плоскости (α1 и α2) заданы общими уравнениями вида: A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, то очевидно, что угол между ними равен углу между их нормалями, то есть между векторами n1={A1,B1,C1) и n2={A2,B2,C2). Получаем, что косинус угла между плоскостями α1 и α2 равен Условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения: A1A2 + B1B2 + C1C2 = 0. Для любой точки М(x,y,z), лежащей на данной прямой, вектор М0М= {x - x0,y - y0,z - z0) коллинеарен направляющему вектору а. Поэтому имеют место равенства: называемые каноническими уравнениями прямой в пространстве. В частности, если требуется получить уравнения прямой, проходящей через две точки: М1(х1, у1, z1) и M2(x2, y2, z2), направляющим вектором такой прямой можно считать вектор М1М2 ={x2 – x1, y2 - y1, z2 - z1}, и уравнения принимают вид: - уравнения прямой, проходящей через две данные точки.
26. Число а называется пределом последовательности Cвойства: 1. Предел суммы .Предел суммы двух функций равен сумме пределов этих функций:
2. Предел произведения функции на постоянную величину Постоянный коэффициент можно выносить за знак предела: 3. Предел постоянной величины. Предел постоянной величины равен самой постоянной величине:
4. Предел произведения. Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют): 5. Предел частного. Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю: 6. Предел степенной функции 7. Предел показательной функции
27. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа e существует такое положительное число d, что при всех х ≠ а, таких, что |x – a | < d, выполняется неравенство Указанный предел обозначается так: Геометрически существование предела функции в точке означает, что для любого числа e > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2d > 0, высотой 2e и центром в точке (а; b), что все точки графика данной функции на интервале (а– d; а + d), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольнике: Функция y=f(x) называется ограниченной на множестве D, если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M. Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D. Функция y=f(x) называется ограниченной при x → a, если существует окрестность с центром в точке а, в которой функция ограничена. Функция y=f(x) называется ограниченной при x→∞, если найдется такое число N>0, что при всех значениях х, удовлетворяющих неравенству |x|>N, функция f(x) ограничена.
28. Функция y = f (x) называется бесконечно малой величиной (Б.М.В.) при Функция y = f (x) называется бесконечно малой величиной при Свойства: 1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая. 2. Произведение бесконечно малых величин есть величина бесконечно малая. 3.Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
29. Функция y = f (x) называется бесконечно большой величиной при Функция y = f (x) называется бесконечно большой величиной при х→∞ , если для каждого положительного сколь угодно большого числа N найдется соответствующее сколь угодно большое число K(N) такое, что для всех х, удовлетворяющих неравенству |x|>K , будет выполняться неравенство |f[x]|>N : Свойства: 1Сумма бесконечно больших величин есть величина бесконечно большая. 2.. Произведение бесконечно больших величин есть величина бесконечно большая. 3.Частное от деления бесконечно большой величины на функцию, имеющую предел в точке х0 , есть величина бесконечно большая. Величина, обратная бесконечно малой величине, есть величина бесконечно большая, и наоборот, величина, обратная бесконечно большой величине, есть величина бесконечно малая. Пусть Символически можно записать:
30. Первый замечательный предел имеет вид: Следствия первого замечательного предела: 1.
31. Второй замечательный предел имеет вид: В случае второго замечательного предела имеем дело с неопределенностью вида Следствия из второго замечательного предела: 1.Замечательный логарифмический предел |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 183. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |












 (а, значит, и ЛЮБАЯ точка данной прямой) не удовлетворяет уравнению плоскости:
(а, значит, и ЛЮБАЯ точка данной прямой) не удовлетворяет уравнению плоскости: 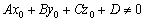 .
.
 , и плоскости
, и плоскости  , которые не лежат на одной прямой, можно составить по формуле:
, которые не лежат на одной прямой, можно составить по формуле:

 =(cos a, cos b, cos y). cos a, cos b, cos y - это некоторые действительные числа, сумма квадратов которых равна единице.
=(cos a, cos b, cos y). cos a, cos b, cos y - это некоторые действительные числа, сумма квадратов которых равна единице. равна единице, а число D неотрицательно.
равна единице, а число D неотрицательно.


 -
- 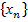 , или пределом переменной xn (обозначается xn→a), если для всякого ɛ>0 найдется зависящее от ɛ число N0 такое, что |xn –a|<ɛ для всех натуральных n >N0.
, или пределом переменной xn (обозначается xn→a), если для всякого ɛ>0 найдется зависящее от ɛ число N0 такое, что |xn –a|<ɛ для всех натуральных n >N0.




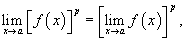 где степень p - действительное число.
где степень p - действительное число. где основание a > 0.
где основание a > 0.

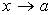 , если ее предел равен нулю
, если ее предел равен нулю 
 , если для каждого положительного сколь угодно малого числа
, если для каждого положительного сколь угодно малого числа  найдется сколь угодно большое положительное число
найдется сколь угодно большое положительное число  такое, что для всех х, удовлетворяющих неравенству
такое, что для всех х, удовлетворяющих неравенству  будет выполняться неравенство
будет выполняться неравенство  :
: 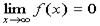
 , если для каждого положительного сколь угодно большого числа N найдется соответствующее сколь угодно малое положительное число y = f (x) такое, что для всех х, удовлетворяющих неравенству
, если для каждого положительного сколь угодно большого числа N найдется соответствующее сколь угодно малое положительное число y = f (x) такое, что для всех х, удовлетворяющих неравенству  , будет выполняться неравенство
, будет выполняться неравенство  :
: 
 .
. и
и  , тогда
, тогда  и
и  .
. и
и  .
.
 2.
2. 
 или в другой записи
или в другой записи 
 .
.