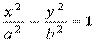Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
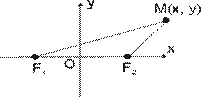
Угол между двумя прямыми. Способ первыйРассмотрим две прямые, заданные уравнениями в общем виде: Самое пристальное внимание обратим на знаменатель – это в точности скалярное произведениенаправляющих векторов прямых: Способ второй Если прямые заданы уравнениями с угловым коэффициентом Условие перпендикулярности прямых выражается равенством 1+k1k2 = 0, откуда, кстати, следует очень полезная взаимосвязь угловых коэффициентов перпендикулярных прямых:k1 = -1/k2 , которая используется в некоторых задачах. Есть и третий способ решения. Идея состоит в том, чтобы вычислить угол между направляющими векторами прямых с помощью формулы: 19. Эллипсом – называется геометрическое место точек на плоскости, сумма расстояний которых до двух заданных точек, называемых фокусами, есть, величина постоянная, большая чем расстояние между фокусами. Комментарии к определению: F1 и F2 – фокусы, | F1F2 | = 2·с — расстояние между фокусами, | MF1 | + |MF2| = 2·a >2·c — определение эллипса.  Избавимся от иррациональности, возведя обе части соотношения в квадрат: Разделив обе части на a2b2, получим каноническое уравнение эллипса Исследование формы эллипса. Так как
Эллипс является симметричным относительно начала координат и относительно осей координат. Это следует из-за того, что в уравнении эллипса переменные x и y входят квадратами x2, y2. Если уравнению эллипса удовлетворяет точка с координатами x и y, то уравнению эллипса будут удовлетворять точки с координатами ( −x, − y), (− x, y), (x, − y).Фокусы эллипса лежат на его большой оси эллипса. 20. Гиперболой называют геометрическое место точек на плоскости, модуль разности расстояний которых до двух заданных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
По условию F1F2 = 2·с, тогда фокусы имеют координаты F1(- с, 0), F2(с, 0). Пусть М(x, y) — произвольная точка гиперболы, и по определению |МF1| − |МF2| = 2 ·a < 2·c. Воспользовавшись формулой расстояния между двумя точками и проведя процедуру избавления от иррациональности, будем иметь: (хс – а2)2 = а2((х – с)2 + у2), х2(с2 – а2) – а2у2 = а2(с2 – а2). Если ввести обозначение b2 = c2 − a2, то уравнение гиперболы примет вид x2·b2 − a2·y2 = a2 b2. Выполнив преобразование, аналогичное выводу уравнения эллипса, получим каноническое уравнение гиперболы:
|
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 165. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и не перпендикулярны, то ориентированный угол q между ними найдем по формуле:
и не перпендикулярны, то ориентированный угол q между ними найдем по формуле: 

 и не перпендикулярны, то ориентированный угол
и не перпендикулярны, то ориентированный угол  между ними найдем по формуле:
между ними найдем по формуле: 
 . Здесь результат заведомо будет положительным. Но может получиться тупой угол. В этом случае придётся из 180-ти градусов вычитать получившийся арккосинус.
. Здесь результат заведомо будет положительным. Но может получиться тупой угол. В этом случае придётся из 180-ти градусов вычитать получившийся арккосинус.
 +
+ 
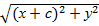 =2а-
=2а- 
 ,
, ,
,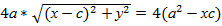 ,
, ,
, ,
, ,
,  .
.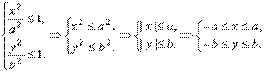 то эллипс лежит внутри прямоугольника со сторонами х = ± а, у = ± b.
то эллипс лежит внутри прямоугольника со сторонами х = ± а, у = ± b.
 -
- 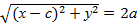 ,
,
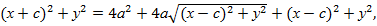
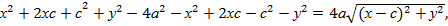
 ,
,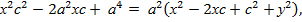

 - а2х2+2а2хс – а2у2 = а2с2 – а4,
- а2х2+2а2хс – а2у2 = а2с2 – а4,