
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства сложения векторов.Стр 1 из 4Следующая ⇒ Разложение определителя По элементам i-й строки:
По элементам j-го столбца:
6. Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Δ = 0. Квадратная матрица В есть обратная матрица для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В. Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратная матрица матрице А, обозначается через А-1, так что В = А-1 и вычисляется по формуле
где А i j - алгебраические дополнения элементов a i j матрицы A.. 7. Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля rang A = K, если Приведём основные методы вычисления ранга матрицы. I. Метод окаймляющих миноров. Пусть в матрице А найден минор М k-го порядка, отличный от нуля. Рассмотрим лишь те миноры (k + 1)-го порядка, которые содержат в себе (окаймляют) минор М: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдётся ненулевой минор (k + 1)-го порядка, и вся процедура повторится. З а м е ч а н и е . Нахождение ранга матриц методом окаймляющих миноров требует вычисления определителей. Поэтому этим методом удобней пользоваться для вычисления ранга матриц небольшого размера. Для вычисления ранга матрицы, у которой число строк и столбцов больше трёх, рациональней использовать метод элементарных преобразований.
8. Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля  rang A = K, если Приведём основные методы вычисления ранга матрицы. Метод элементарных преобразований Элементарными преобразованиями матрицы называют следующие: 1. Перестановка строк (столбцов). 2. Умножение строки (столбца) на число, отличное от нуля. 3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число. 4. Вычёркивание строки (столбца), все элементы которой равны нулю. З а м е ч а н и е . 1) Элементарные преобразования не меняют ранга матрицы; 2) матрицы, полученные одна из другой путём элементарных преобразований, называются эквивалентными (обозначаются A ~ В). Чтобы вычислить ранг матрицы А, путём элементарных преобразований сводим её к ступенчатому виду (в частности к треугольному), выделяя наибольший минор, отличный от нуля.
А~
rangA = rangB= k
9. Пусть дана система n линейных уравнений с n неизвестными Правило Крамера Введем для системы линейных уравнений следующие матрицы:
10. Пусть дана система n линейных уравнений с n неизвестными Предположим, что среди коэффициентов
11. Для задания декартовой прямоугольной системы координат нужно выбрать несколько взаимноперпендикулярных прямых, называемых осями. Точка пересечения осей O называется началом координат. На каждой оси нужно задать положительное направление и выбрать единицу масштаба. Координаты точки P считаются положительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P.
Декартовыми прямоугольными координатами точки P на плоскости называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных прямых - осей координат или, что то же, проекции радиус-вектора r точки P на две взаимно перпендикулярные координатные оси. Когда говорят про двухмерную систему коодинат, горизонтальную ось называют осью абсцисс (осью Ox), вертикальную ось - осью ординат (осью Оy). Положительные направления выбирают на оси Ox - вправо, на оси Oy - вверх. Координаты x и y называются соответственно абсциссой и ординатой точки. Запись P(a,b) означает, что точка P на плоскости имеет абсциссу a и ординату b. Декартовыми прямоугольными координатами точки P в трехмерном пространстве называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до трех взаимно перпендикулярных координатных плоскостей или, что то же, проекции радиус-вектора r точки P на три взаимно перпендикулярные координатные оси. В зависимости от взаимного расположения положительных направлений координатных осей возможны левая и правая координатные системы.
Как правило, пользуются правой координатной системой. Положительные направления выбирают: на оси Ox - на наблюдателя; на оси Oy - вправо; на оси Oz - вверх. Координаты x, y, z называются соответственно абсциссой, ординатой и аппликатой. Координатными поверхностями, для которых одна из координат остается постоянной, здесь являются плоскости, параллельные координатным плоскостям, а координатными линиями, вдоль которых меняется только одна координата, - прямые, параллельные координатным осям. Координатные поверхности пересекаются по координатным линиям. Запись P(a,b,c) означает, что точка Q имеет абсциссу a, ординату b и аппликату c.
Полярными координатами точки P называются радиус-вектор ρ - расстояние от точки P до заданной точки O (полюса) и полярный угол φ - угол между прямой OP и заданной прямой, проходящей через полюс (полярной осью). Полярный угол считается положительным при отсчете от полярной оси против часовой стрелки и отрицательным при отсчете в обратную сторону. Координатные линии в полярных системах - окружности с центром в полюсе и лучи. Формулы для перехода от полярных координат к декартовым x=ρ*cos(φ), y=ρ*sin(φ) и обратно: ρ=sqrt(x2)+y2), φ=arctg(y/x)=arcsin(y/ρ)
12. Вектором называется направленный отрезок, для которого указано его начало и конец: Произведением ненулевого вектора Правило сложения векторов по правилу треугольников: Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор Свойства сложения векторов. 1. Сложение векторов подчиняется закону ассоциативности: (a+b)+c = a+(b+c) 2. Существует нулевой элемент относительно сложения векторов: a+(-a) = (-a)+a =0 3. Для любого вектора существует противоположный ему вектор, такой, что a+(-a)=(-a)+a=0 4. Сложение векторов подчиняется закону коммутативности: а+b =b+a 5.Первое распределительное свойство .(a+b)*c = a*c+b*c . Чтобы из вектора а вычесть вектор b надо к вектору а прибавить вектор, противоположный вектору b. Полученный в результате этой операции вектор си будет являться разностью векторов аи b. Таким образом, с = а − b = а + (− b).
Любой вектор ⃗𝑝 можно разложить, и притом единственным образом, по двум данным неколлинеарным векторам ⃗𝑎 и ⃗𝑏 ⃗𝑝 = 𝑥⃗𝑎 + 𝑦⃗𝑏. 1. В треугольнике 𝐴𝐵𝐶 медианы 𝐴𝑀 и 𝐶𝑁 пересекаются в точке 𝑂. Разложите по базисным векторам ⃗𝑚 = 𝑂𝐴 и ⃗𝑛 = 𝑂𝐶 следующие векторы: 𝑂𝑁, 𝐴𝐶, 𝐵𝐴, 𝐵𝑂. 2. В прямоугольнике 𝐴𝐵𝐶𝐷 точка 𝐹 делит сторону 𝐵𝐶 в отношении 2 : 3, считая от 𝐵. Разложите 𝐴𝐹 по 𝐵𝐴 и 𝐷𝐴. 3. В правильном шестиугольнике 𝐴𝐵𝐶𝐷𝐸𝐹 известно, что 𝐴𝐵 = ⃗𝑎, 𝐴𝐹 =⃗𝑏. Найдите векторы 𝐴𝐷, 𝐵𝐷, 𝐹𝐷 и 𝐵𝑀, где 𝑀 — середина стороны 𝐸𝐹.
13. Скалярным произведением ⃗𝑎* ⃗b векторов ⃗𝑎 и ⃗b называется число (скаляр) равное произведению их длин (модулей), умноженному на соs угла между ними: ⃗𝑎* ⃗b = | ⃗𝑎|*| ⃗b|*cos(⃗𝑎,Ù ⃗b). Свойства скалярного произведения: 1) ⃗𝑎* ⃗b = ⃗b* ⃗a – коммутативность (переместительный закон); 2)(l ⃗𝑎)* ⃗b = l( ⃗𝑎* ⃗b) –ассоциацивность относительно числового множителя(сочетательный закон); 3) ⃗𝑎*( ⃗b+¯с) = ⃗𝑎* ⃗b+ ⃗𝑎* ⃗с – дистрибутивность (распределительный закон); 4) ⃗𝑎* ⃗b= 0 – необходимое и достаточное условие перпендикулярности ненулевых векторов; 5) ⃗𝑎* ⃗а= ⃗𝑎2 = | ⃗a|2 – скалярный квадрат вектора.
14. Векторным произведением ⃗𝑎* ⃗b векторов ⃗𝑎 и ⃗b называется вектор ⃗с, определяемый следующими условиями: 1.| ⃗c| = | ⃗𝑎|*| ⃗b|*sin(⃗𝑎,Ù ⃗b). 2.Вектор ⃗с ортогонален каждому из векторов ⃗𝑎, ⃗b. 3.Векторы ⃗𝑎, ⃗b, ⃗с образуют правую тройку. Свойства векторного произведения: 1) ⃗𝑎* ⃗b = - ⃗b* ⃗a – антикоммутативность ; 2)(l ⃗𝑎)* ⃗b = l( ⃗𝑎* ⃗b) – ассоциацивность относительно числового множителя; 3) ⃗𝑎*( ⃗b+¯с) = ⃗𝑎* ⃗b+ ⃗𝑎* ⃗с – дистрибутивность ; 4) ⃗𝑎* ⃗b= 0 – необходимое и достаточное условие перпендикулярности ненулевых векторов;
15. Смешанным произведением ⃗𝑎 ⃗b ⃗с векторов ⃗𝑎, ⃗b, ⃗с называется число, равное векторному произведению ⃗𝑎* ⃗b, умноженному скалярно на вектор ⃗с, т.е. ⃗𝑎 ⃗b ⃗с = (⃗𝑎* ⃗b)* ⃗с. Геометрический смысл смешанного произведения. Модуль ⃗|𝑎 ⃗b ⃗с| равен объему параллелепипеда, построенного на векторах ⃗𝑎, ⃗b, ⃗с. Свойства смешанного произведения: 1. ⃗𝑎 ⃗b ⃗с = ( ⃗𝑎* ⃗b)* ⃗с = ⃗𝑎*( ⃗b* ⃗с); 2. ⃗𝑎 ⃗b ⃗с = . ⃗b ⃗c ⃗a =. ⃗c ⃗a ⃗b = - ⃗b ⃗a ⃗с = - ⃗𝑎 ⃗c ⃗b; 3. (l ⃗𝑎) ⃗b ⃗с = l( ⃗𝑎 ⃗b ⃗с); 4. ⃗𝑎 ⃗b( ⃗с + ⃗d) = ⃗𝑎 ⃗b ⃗с + ⃗𝑎 ⃗b ⃗d; 5. ⃗𝑎 ⃗b ⃗с = 0 – необходимое и достаточное условие компланарности векторов ⃗𝑎, ⃗b, ⃗с.
16. Уравнение прямой на плоскости в прямоугольной системе координат Oxy есть некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой. Вид уравнения прямой в прямоугольной системе координат Oxy на плоскости задает теорема: Всякое уравнение первой степени с двумя переменными x и y вида Ах +Ву+С =0, где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида Ах +Ву+С =0 - называется общим уравнением прямой на плоскости. Уравнение прямой вида y =k*x+b, где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент). Определение углового коэффициента прямой дается через определение угла наклона прямой к положительному направлению оси Ox. Углом наклона прямой к положительному направлению оси абсцисс в данной прямоугольной декартовой системе координат Oxy называют угол а, отсчитываемый от положительного направления оси Ох до данной прямой против хода часовой стрелки. Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть, k = tg a. Параметрические уравнения прямой на плоскости имеют вид Параметрические уравнения прямой устанавливают неявную зависимость между абсциссами и ординатами точек прямой линии с помощью параметра l(отсюда и название этого вида уравнений прямой). Пара чисел (х,у), которые вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра l, представляет собой координаты некоторой точки прямой. 17. Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть, k = tg a. Уравнение прямой с угловым коэффициентом имеет вид y =k*x+b, Уравнение прямой, проходящей через данную точку A(x1, y1) в данном направлении, определяемом угловым коэффициентом k, y - y1 = k(x - x1). Это уравнение определяет пучок прямых, проходящих через точку A(x1, y1), которая называется центром пучка. Уравнение прямой, проходящей через две точки: A(x1, y1) и B(x2, y2), записывается так:
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле
Если в общем уравнении прямой вида Ax+By +C =0 числа А, В и С таковы, что длина вектора Часто можно видеть другую форму записи нормального уравнения прямой: cosa *x + cosb *y – p = 0, где cosa и cosb - действительные числа, представляющие собой направляющие косинусы нормального вектора прямой единичной длины (то есть,
18. Расстояние от точки M(x0;у0) до прямой d: Ax+By+C =0 выражается формулой |
||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 222. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 ,
, , Mk+1= 0 , Mk+2= 0,....
, Mk+1= 0 , Mk+2= 0,....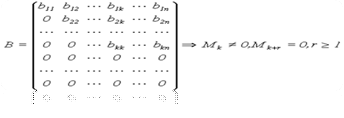


 ,
, при неизвестном х1 имеются коэффициенты, отличные от нуля. Пусть одним из таких коэффициентов является а11. Разделим первое уравнение системы на а11, получим:
при неизвестном х1 имеются коэффициенты, отличные от нуля. Пусть одним из таких коэффициентов является а11. Разделим первое уравнение системы на а11, получим: (2)
(2)  (3)
(3)  . Из последнего уравнения системы (3) найдем хn. Подставляя затем это значение в предыдущее уравнение, найдем х n -1 и т.д. Продолжая эту процедуру, дойдем до первого уравнения, из которого путем подстановки уже найденных значений х2, х3, …, х n получим неизвестное х1.
. Из последнего уравнения системы (3) найдем хn. Подставляя затем это значение в предыдущее уравнение, найдем х n -1 и т.д. Продолжая эту процедуру, дойдем до первого уравнения, из которого путем подстановки уже найденных значений х2, х3, …, х n получим неизвестное х1.



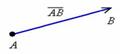 В данном случае началом отрезка является точка
В данном случае началом отрезка является точка 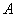 , концом отрезка – точка
, концом отрезка – точка  .
. на число
на число  является такой вектор
является такой вектор 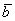 , длина которого равна
, длина которого равна  , причём векторы
, причём векторы  и противоположно направлены при
и противоположно направлены при  .
. Суммой векторов
Суммой векторов  .
. , где х 1 ,у 1, а х и а у– некоторые действительные числа, причем а х и а у одновременно не равны нулю, а l- параметр, принимающий любые действительные значения.
, где х 1 ,у 1, а х и а у– некоторые действительные числа, причем а х и а у одновременно не равны нулю, а l- параметр, принимающий любые действительные значения.







 = =(A,B) равна единице, а C ≤ 0 , то это общее уравнение прямой называется нормальным уравнением прямой. Нормальное уравнение прямой определяет в прямоугольной системе координат Oxy прямую линию, нормальным вектором которой является вектор
= =(A,B) равна единице, а C ≤ 0 , то это общее уравнение прямой называется нормальным уравнением прямой. Нормальное уравнение прямой определяет в прямоугольной системе координат Oxy прямую линию, нормальным вектором которой является вектор  = (A,B) , причем эта прямая проходит на расстоянии |C| от начала координат в направлении вектора
= (A,B) , причем эта прямая проходит на расстоянии |C| от начала координат в направлении вектора 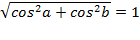 ), а величина p (p ≥ 0 ) равна расстоянию от начала координат до прямой.
), а величина p (p ≥ 0 ) равна расстоянию от начала координат до прямой. .
.