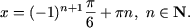Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Производная и первообразная
Правила вычисления производных
Уравнение касательной
Показательная функция
Показательные уравнения
где a > 0, a ≠ 1. Утверждение 1. Уравнение (1) имеет единственное решение x = logab при b > 0 и не имеет решений при b ≤ 0. Пример 1. Решить уравнения: a) 2x = -4, b) 2x = 4, c) 2x = 5. Решение. a) Множество решений данного уравнения пусто, так как левая часть уравнения положительна при любом x Î R (см. свойства показательной функции), а правая часть есть отрицательное число. b) Используя утверждение 1, получим x = log24, то есть x = 2. c) Аналогично предыдущему примеру получим x = log25.
где a > 0, a ≠ 1 и b > 0 равносильно уравнению f(x) = logab. Пример 2. Решить уравнение Решение. Согласно замечанию к утверждению 1
Так как
и f(x) = g(x) равносильны. Показательные неравенства. При решении показательныx неравенств используются следующие утверждения: A.1. Если a > 1, неравенство a f(x) > a g(x) равносильно неравенству f(x) > g(x). Аналогично, a f(x) < a g(x) Û f(x) < g(x). A.2. Если 0 < a < 1, неравенство  a f(x) > a g(x) равносильно неравенству f(x) < g(x). Аналогично, a f(x) < a g(x) Û f(x) > g(x). A.3. Неравенство
равносильно совокупности систем неравенств
A.4. Если b ≥ 0, неравенство af(x) < b не имеет решений (следует из свойств показательной функции). A.5. Если b ≤ 0, множеством решений неравенства af(x) > b является x Î D(f). A.6. Если a > 1, b > 0, неравенство af(x) > b равносильно неравенству f(x) > logab. Аналогично, a f(x) < b Û f(x) < logab. A.7. Если 0 < a < 1, b > 0, неравенство a f(x) > b равносильно неравенству f(x) < logab. Аналогично, a f(x) < b Û f(x) > logab. Логарифмы
Логарифмическая функция непрерывна и строго возрастает (если основание a > 1) или строго убывает (если a < 1) на всей области определения. Множество ее значений – все действительные числа.
Логарифм по основанию e называется натуральным и обозначается ln x. Логарифм по основанию 10 называется десятичным и обозначается lg x. Логарифмические уравнения Простейшим логарифмическим уравнением является уравнение вида
Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = ab. Утверждение 2. Уравнение loga f(x) = loga g(x) (a > 0, a ≠ 1) равносильно одной из систем (очевидно, выбирается та система, неравенство которой решается проще)
Утверждение 3. Уравнение logh(x) f(x) = log h(x) g(x) равносильно одной из систем
При решении логарифмических уравнений полезно использовать равносильные преобразования. В противном случае, проверка полученных решений является составной частью решения. Более того, необходимо учитывать и преобразования, которые могут привести к потере корней. |
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 206. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
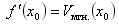


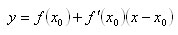



 1
1

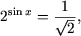

 , следовательно
, следовательно  , откуда
, откуда