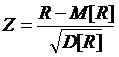Двувыборочный критерий Уилкоксона-Манна-Уитни

НЕПАРАМЕТРИЧЕСКОЕ ОЦЕНИВАНИЕ 

ЭКСПЕРИМЕНТАЛЬТНЫХ ДАННЫХ

Саратов 2016

Общие положения

Если по результатам проведения экспериментальных исследований объем получаемых данных является небольшим, то применение стандартных параметрических процедур статистического анализа, основанных на предположении о принадлежности данных нормальной генеральной совокупности, становится невозможным ввиду невозможности выполнения процедуры статистической проверки гипотез о распределении. В этом случае применяются процедуры, которые не зависят от вида распределения и предназначены для решения задач статистического анализа данных непараметрическими методами.

Непараметрические процедуры используют знаки и знаковые ранги исходных данных, что приводит к неизбежной потере некоторой доли информации, поэтому для нормально распределенных данных эффективность непараметрических процедур будет ниже эффективности процедур параметрических. Для данных же, имеющих распределение, отличное от нормального, т.е. содержащих тренды (тенденции), эффективность непараметрических процедур по сравнению с параметрическими может быть сколь угодно большой. Непараметрические процедуры устойчивы к аномальным наблюдениям и пригодны для данных с разнораспределенными ошибками.

Применение непараметрических методов также требует непрерывности распределения изучаемой совокупности, но не основывается на предположении о каком-либо конкретном виде этого распределения. В этих методах среднее значение во многом теряет смысл и вместо него рассматривается медиана. Медиана имеет два преимущества перед средним значением. Во-первых, она всегда существует в виде точки, разделяющей распределение совокупности пополам, в то же время как среднее значение может не существовать (например, в случае равномерного распределения или распределения Коши). Во-вторых, медиана весьма устойчива к большим возмущениям исходного распределения. Следовательно, если в генеральной совокупности есть выбросы или грубые ошибки, их влияние на медиану будет невелико, тогда как среднее значение может измениться очень сильно.

Важным свойством непараметрических методов является простота вычисления соответствующих статистик, а также то, что они приводят к процедурам проверки гипотез с уровнями значимости, которые могут быть определены при любом распределении генеральной совокупности. Следует отметить асимптотическую нормальность этих статистик, то есть нормальность при неограниченном увеличении объема выборки, которая упрощает статистический анализ.

Непараметрические методы позволяют решать различные задачи, в частности, проверки гипотезы о принадлежности экспериментальных данных одному и тому же непрерывному распределению (двувыборочный критерий Уилкоксона-Манна-Уитни), совпадения средних значений нескольких совокупностей данных (однофакторный дисперсионный анализ Крускала-Уоллиса), определения меры связи между данными с помощью ранговых корреляций для парных (коэффициент Кендалла) и многомерных (коэффициент конкордации) совокупностей. Рассмотрим эти методы [1].

Двувыборочный критерий Уилкоксона-Манна-Уитни

Двувыборочные критерии позволяют решать вопрос о том, имеют ли две совокупности одно и то же непрерывное распределение с центром в одной и той же точке. Они являются критериями проверки гипотезы

H₀: F(z) = G(z) для всех z

против

H₁: F(z) ¹ G(z) хотя бы для некоторых z.

В нормальной параметрической теории их аналогами является двувыборочный t-критерий Стьюдента. Рассмотрим наиболее мощный критерий Уилкоксона-Манна-Уитни, который применяется для проверки идентичности двух совокупностей.

Пусть x₁, …, x_n1 – случайная выборка из 1 совокупности, а y₁, …, y_n2 – выборка из второй совокупности. Обе совокупности имеют непрерывные функции распределения. Запишем эти выборки в виде объединенного вариационного ряда, т.е. в виде совокупности всех наблюдений, расставленных в порядке возрастания их величин, без учета принадлежности к выборке. Каждое упорядоченное таким образом наблюдение отмечается символом x или y в соответствии с тем, из какой выборки взято это наблюдение. Если в какой-либо из выборок окажутся среди наблюдений окажутся равные величины, то им приписываются средние ранги. В результате получается ряд, содержащий n₁ символов x и n₂ символов y, перемешанных между собой. Затем полученному ряду присваиваются ранги, и подсчитывается сумма рангов рядов с символами x и y.

Ранги, соответствующие элементам первой выборки в объединенном вариационном ряду, обозначаются r₁, …, r_n1, второй – s₁, …, s_n2. Статистика Уилкоксона-Манна-Уитни – это сумма рангов одной из выборок

или

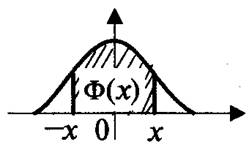
Если известна одна из статистик, то другая определяется однозначно, поэтому проще пользоваться статистикой из выборки с меньшим объемом.

Если верна гипотеза H₀, что F и G являются одной и той же функцией распределения, то не следует ожидать концентрации наблюдений из одной выборки на одном из концов объединенного вариационного ряда: их значения должны быть рассеяны по всему ряду. Для альтернативной гипотезы H₁ сравнительно малые и большие значения выбранной статистики (например, R₁) должны заставить усомниться в правильности гипотезы H₀.

Критическая область. Верхняя 2,5%-я область стандартного нормального распределения (рис.1).

Рис.1. Двусторонняя область проверки гипотез

для нормального распределения

Так как дисперсии статистик R₁ и R₂ равны, то можно использовать любую из них с математическими ожиданиями

и дисперсией

Статистика

(5)

при H₀ асимптотически нормальна N(0, 1). 

Асимптотическая эффективность критерия Уилкоксона-Манна-Уитни относительно критерия Стьюдента (t-критерия) равна 3/π ≈ 0,955 при условии, что оба критерия применяются к нормальным совокупностям с однородными дисперсиями. Таким образом, преимущество критерия Стьюдента невелико; если же данные отклоняются от нормального закона, то критерий Уилкоксона-Манна-Уитни может оказаться более мощным.