
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интегралы с бесконечными пределами. ⇐ ПредыдущаяСтр 4 из 4 Если функция Если предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся. Несобственный интеграл
Признаки сходимости и расходимости. 1. Пусть при 2.Если Аналогично устанавливаются признаки сходимости и расходимости интеграла В задачах 7.205-7.213 вычислить несобственные интегралы (или установить их расходимость). 7.205 7.208 7.211 В задачах 7.214-7.219,используя признаки сходимости, исследовать сходимость следующих интегралов: 7.214 7.217 Интегралы от неограниченных функций. Если функция Если предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся. Признаки сходимости и расходимости. 1. Пусть при 2.Если Аналогично устанавливаются признаки сходимости и расходимости  В задачах 7.220-7.228 вычислить несобственные интегралы (или установить их расходимость). 7.220 7.223 7.226 В задачах 7.229-7.234,используя признаки сходимости, исследовать сходимость следующих интегралов: 7.229 7.232 Некоторые приложения определенного интеграла. Геометрические приложения определённого интеграла. Площадь фигуры
Площадь фигуры
Если фигура ограничена кривой, заданной параметрическими уравнениями Площадь криволинейного сектора В задачах 7.235-7.238 вычислить площади фигур, ограниченных линиями, заданными в прямоугольных координатах: 7.235 а) в) 7.236 а) 7.237 а) б) 7.238 а) в) 7.239Найти площадь фигуры, ограниченной параболой В задачах 7.240-7.243 вычислить площади плоских фигур, ограниченных линиями: а) заданными параметрически; б) заданными в полярных координатах. 7.240 а) б) 7.241 а) б) 7.242 а) б) 7.243 а) б) 7.244Найти площадь фигуры, ограниченной лемнискатой 7.245 Найти площадь фигуры, ограниченной окружностью
Длина дуги плоской кривой Длина дуги плоской кривой, заданной параметрическими уравнениями Длина дуги пространственной кривой, заданной параметрическими уравнениями
Длина дуги плоской кривой, заданной в полярных координатах уравнением В задачах 7.246-7.249найти длины дуг следующих кривых: 7.246 а) б) в) 7.247 а) б) в) 7.248 а) б) в) 7.249 а) б) в) 7.250На циклоиде Площадь поверхности, образованной вращением вокруг оси Площадь поверхности, образованной вращением вокруг оси При параметрическом задании дуги кривой
Площадь поверхности, образованной вращением вокруг полярной оси (оси В задачах 7.251-7.253найти площади поверхностей, образованных вращением кривых 7.251 а) б) в) 7.252 а) б) вокруг оси в) 7.253 а) б) в) Если Объём тела, образованного вращением вокруг оси Объём тела, образованного вращением вокруг оси Объём тела, образованного вращением вокруг оси 7.254Вычислить объёмы тел, ограниченных поверхностями: а) в) г) В задачах 7.255-7.260 вычислить объемы тел, полученных вращением плоской фигуры Ф , ограниченной указанными линиями вокруг: а) оси 7.255 Ф: 7.256 Ф: 7.258 Ф: 7.259Ф: 7.260 Ф: 7.261Найти объём тела, образованного вращением вокруг оси 7.262Найти объём тела, образованного вращением параболического сегмента с основанием Приложения определенного интеграла к решению некоторых задач механики, физики и экономики. Статические моменты
При параметрическом задании дуги кривой
Путь Работа Объём продукции Издержки производства 7.263Найти статический момент синусоиды 7.264Найти статический момент и момент инерции относительно оси Ох дуги кривой 7.265Найти статический момент и момент инерции полуокружности радиуса а относительно ее диаметра. 7.266Найти статический момент и момент инерции относительно оси Ох одной арки циклоиды 7.267Найти координаты центра масс дуги окружности 7.268Найти координаты центра масс дуги астроиды 7.269Найти массу стержня длины 7.270Скорость прямолинейного движения тела выражается формулой 7.271Вычислить путь, пройденный свободно падающим в пустоте телом за 7.272Скорость тела, брошенного вертикально вверх с начальной скоростью 7.273Какую работу надо затратить (в 7.274Сила тока, измеряемая в амперах, определяется формулой 7.275Найти количество тепла 7.276Сила переменного тока меняется по закону 7.277Найти среднее значение издержек производства некоторой продукции при заданном изменении объёма производства а) б) 7.278Доход от инвестиций в некоторое производство равен нулю в течение первого года, а затем изменяется по закону 7.279Найти среднее значение издержек производства и объём продукции 7.280Определить объём продукции, произведённой рабочим за указанный промежуток времени рабочего дня, если производительность труда характеризуется функцией |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 211. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
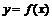 интегрируема на отрезке
интегрируема на отрезке 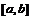 , то несобственным интегралом первого рода от функции
, то несобственным интегралом первого рода от функции 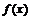 на промежутке
на промежутке 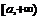 называется
называется 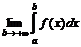 и обозначается
и обозначается 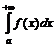 , т.е.
, т.е. 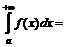
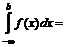
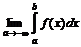 .
.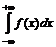 определяется равенством:
определяется равенством: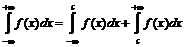 , где
, где 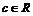 - произвольное число, причём интеграл в левой части равенства сходится, если сходятся оба интеграла в правой части.
- произвольное число, причём интеграл в левой части равенства сходится, если сходятся оба интеграла в правой части.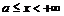
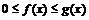 . Тогда, если
. Тогда, если 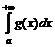 сходится, то сходится и
сходится, то сходится и 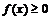 и
и 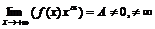 , т.е.
, т.е. 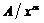 при
при 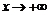 , то: 1) при
, то: 1) при 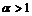
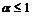 расходится.
расходится.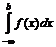 .
.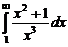 . 7.206
. 7.206 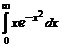 . 7.207
. 7.207 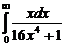 .
.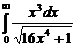 . 7.209
. 7.209 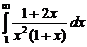 . 7.210
. 7.210 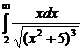 .
.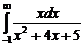 . 7.212
. 7.212 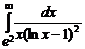 . 7.213
. 7.213 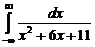 .
.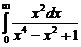 . 7.215
. 7.215 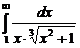 . 7.216
. 7.216 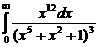 .
.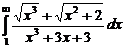 7.218
7.218 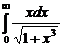 7.219
7.219 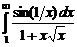 .
.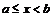 и
и 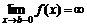 , то несобственным интегралом второго рода от функции
, то несобственным интегралом второго рода от функции 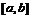 называется
называется 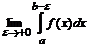 и обозначается
и обозначается 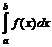 , т.е.
, т.е. 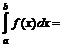
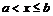 и
и 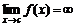 :
:  .
.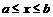
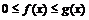 ,
, 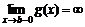 . Тогда, если
. Тогда, если 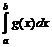 сходится, то сходится и
сходится, то сходится и 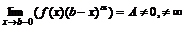 , т.е.
, т.е. 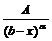 при
при 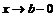 , то: 1) при
, то: 1) при 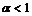
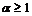 расходится.
расходится.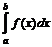 при
при 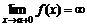 ,
, 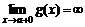 .
.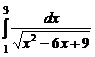 . 7.221
. 7.221 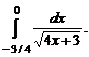 7.222
7.222 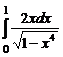 .
.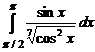 . 7.224
. 7.224 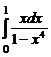 . 7.225
. 7.225 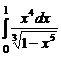 .
.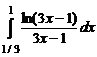 . 7.227
. 7.227 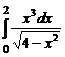 . 7.228
. 7.228 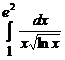 .
.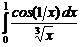 . 7.230
. 7.230 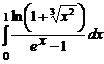 . 7.231
. 7.231 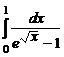 .
.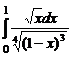 . 7.233
. 7.233 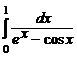 . 7.234
. 7.234 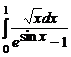 .
.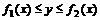 равна
равна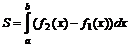 .
.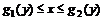 ,
, 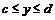 равна
равна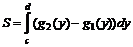 .
.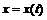 ,
, 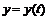 , прямыми
, прямыми 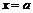 ,
, 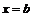 и осью
и осью 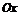 , то её площадь равна
, то её площадь равна 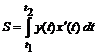 , где
, где 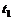 и
и 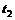 определяются из уравнений
определяются из уравнений 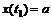 ,
, 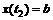 (
( 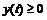 на отрезке
на отрезке 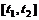 ).
).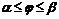 ,
, 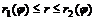 , где
, где 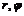 - полярные координаты, равна
- полярные координаты, равна 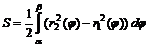 .
.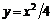 ,
, 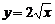 ; б)
; б) 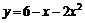 ,
, 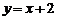 ;
;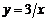 ,
, 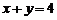 .
.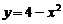 ,
, 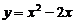 ; б)
; б) 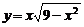 ,
, 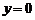 ;
; 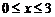 в)
в)  ,
, 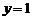 ,
, 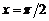 ,
, 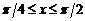 .
.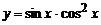 ,
, 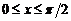 ;
; 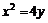 ,
, 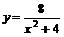 ; в)
; в)  ,
, 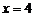 ,
, 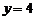 ,
, 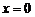 ,
, 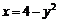 ,
, 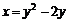 ; б)
; б) 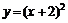 ,
, 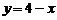 ;
; 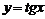 ,
,  ,
, 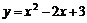 , касательной к ней в точке
, касательной к ней в точке 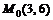 и осями координат
и осями координат 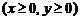 .
.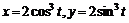 (астроида);
(астроида);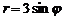 ,
, 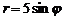 (окружности).
(окружности). 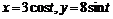 (эллипс) и
(эллипс) и 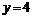
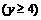 ;
;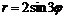 (трилистник) .
(трилистник) . 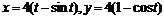
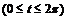 (циклоида)и
(циклоида)и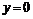 ;
;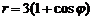 (кардиоида)
(кардиоида) 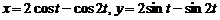 (кардиоида);
(кардиоида); 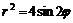 (лемниската).
(лемниската). 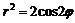 и окружностью
и окружностью 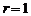
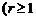 ).
).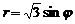 и кардиоидой
и кардиоидой 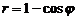 (вне кардиоиды).
(вне кардиоиды).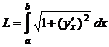
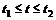 , равна
, равна 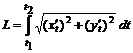 .
.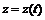 ,
, 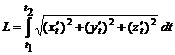 .
.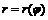 ,
, 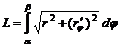 .
.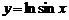
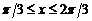 ;
;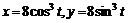
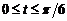 (астроида);
(астроида);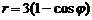 (кардиоида).
(кардиоида).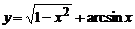
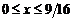 ;
;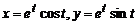
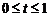
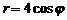 (окружность).
(окружность).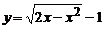
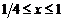 ;
;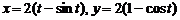
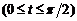 (циклоида)
(циклоида)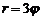
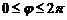 (спираль Архимеда).
(спираль Архимеда).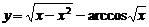
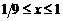 ;
;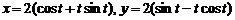
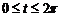 ;
;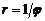
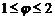 (гиперболическая спираль) .
(гиперболическая спираль) .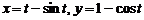 найти точку
найти точку  , которая делит длину первой арки циклоиды в отношении
, которая делит длину первой арки циклоиды в отношении 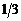 , считая от начала координат.
, считая от начала координат.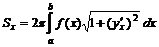 .
.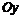 дуги кривой
дуги кривой 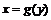 ,
, 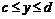 , равна
, равна 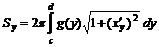 .
.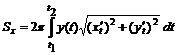 ,
, 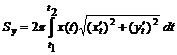 .
.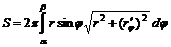 .
.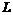 вокруг указанной оси.
вокруг указанной оси.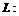
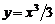 ,
, 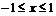 вокруг оси
вокруг оси 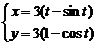
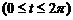 (циклоида) вокруг оси
(циклоида) вокруг оси 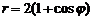 (кардиоида) вокруг полярной оси.
(кардиоида) вокруг полярной оси.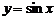 ,
, 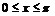 вокруг оси
вокруг оси 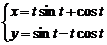
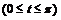 (эвольвента окружности)
(эвольвента окружности) 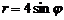 (окружность) вокруг полярной оси.
(окружность) вокруг полярной оси.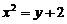 ,
, 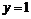 вокруг оси
вокруг оси 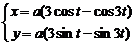
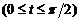 вокруг оси
вокруг оси 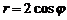 (окружность) вокруг полярной оси.
(окружность) вокруг полярной оси.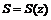 - площадь сечения тела плоскостью, перпендикулярной к оси
- площадь сечения тела плоскостью, перпендикулярной к оси 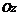 , в точке с аппликатой
, в точке с аппликатой 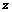 , то объём этого тела равен
, то объём этого тела равен 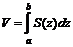 , где
, где 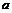 и
и 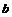 - аппликаты крайних сечений тела.
- аппликаты крайних сечений тела.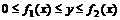 равен
равен 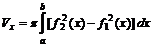 .
.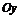 плоской фигуры
плоской фигуры 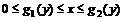 ,
, 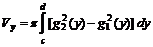 .
.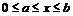 ,
, 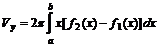 .
.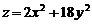 ,
, 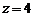 ; б)
; б) 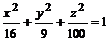 ,
,  ,
, 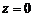 ;
;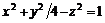 ,
, 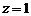 ,
, 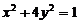 ,
, 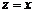
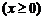 ,
, 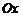 ; б) оси
; б) оси 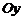 .
.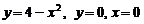
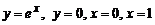 . 7.257 Ф:
. 7.257 Ф: 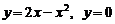 .
.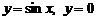
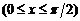 .
.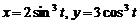
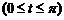 (циклоида).
(циклоида).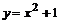 ,
, 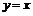 ,
, 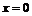 ,
, 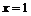 .
.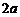 и высотой
и высотой 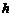 вокруг высоты.
вокруг высоты.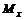 и
и 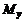 , моменты инерции
, моменты инерции 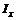 и
и 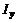 , масса
, масса 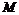 , координаты
, координаты 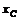 и
и 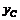 центра масс
центра масс 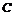 дуги кривой
дуги кривой 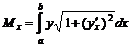 ,
, 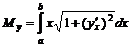 ,
,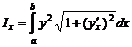 ,
, 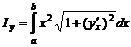 ,
,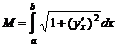 ,
, 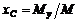 ,
, 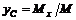 .
.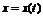 ,
, 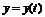 ,
, 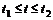 :
: 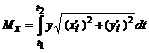 ,
, 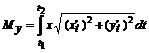 ,
, 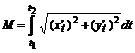
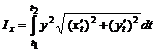 ,
, 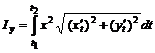 .
.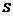 , пройденный телом со скоростью
, пройденный телом со скоростью 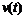 за отрезок времени
за отрезок времени 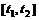 , равен
, равен 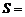
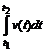 .
.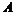 переменной силы
переменной силы 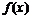 , действующей вдоль оси
, действующей вдоль оси 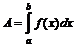 .
.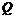 , произведённой за отрезок времени
, произведённой за отрезок времени 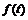 , равен
, равен 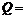
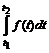 .
.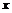 производства
производства 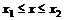 равны
равны 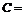
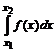
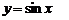
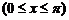 относительно оси Ох.
относительно оси Ох.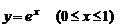 .
.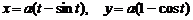 .
.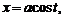
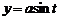 , расположенной в первой четверти.
, расположенной в первой четверти.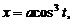
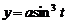 , расположенной выше оси Ох.
, расположенной выше оси Ох.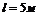 , если линейная плотность стержня меняется по закону
, если линейная плотность стержня меняется по закону 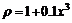 (кг/м3) , где
(кг/м3) , где 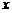 - расстояние от одного из концов стержня.
- расстояние от одного из концов стержня.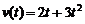 (м/сек). Найти путь
(м/сек). Найти путь 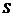 , пройденный телом за
, пройденный телом за 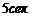 от начала движения.
от начала движения.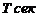 , если известно, что скорость
, если известно, что скорость 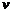 свободного падения в пустоте определяется формулой
свободного падения в пустоте определяется формулой 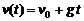 , где
, где 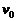 - начальная скорость тела,
- начальная скорость тела, 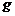 - ускорение свободного падения.
- ускорение свободного падения.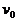 , без учета сопротивления воздуха равна
, без учета сопротивления воздуха равна 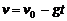 , где t- протекшее время, g- ускорение свободного падения. На какую максимальную высоту поднимется тело?
, где t- протекшее время, g- ускорение свободного падения. На какую максимальную высоту поднимется тело?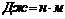 ), чтобы растянуть пружину на
), чтобы растянуть пружину на 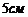 , если сила в
, если сила в 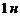 растягивает её на
растягивает её на 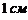 (Указание: по закону Гука сила прямо пропорциональна растяжению пружины).
(Указание: по закону Гука сила прямо пропорциональна растяжению пружины).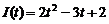 . Найти количество электричества (в кулонах), протекшее через поперечное сечение проводника за
. Найти количество электричества (в кулонах), протекшее через поперечное сечение проводника за 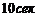 , считая время от начала опыта.
, считая время от начала опыта.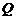 , выделяемое переменным током
, выделяемое переменным током 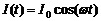 за время
за время 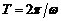 в проводнике с сопротивлением
в проводнике с сопротивлением 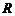 (Указание: по закону Джоуля-Ленца количество тепла, выделяемой постоянным током за время
(Указание: по закону Джоуля-Ленца количество тепла, выделяемой постоянным током за время 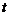 , равно
, равно 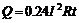 ).
).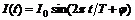 , где
, где 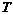 -период. Найти среднее значение силы тока за полупериод
-период. Найти среднее значение силы тока за полупериод  .
.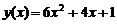 ,
, 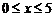 ;
;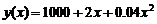 ,
, 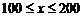 .
.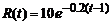 , где
, где 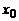 , при котором издержки, задаваемые функцией
, при котором издержки, задаваемые функцией 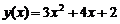 ,
, 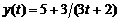 : а)за пятый час рабочего дня; б)за первые 3 часа рабочего дня.
: а)за пятый час рабочего дня; б)за первые 3 часа рабочего дня.