
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определённый интеграл и методы его вычисления. К понятию определённого интеграла можно прийти, решая задачу о вычислении площади криволинейной трапеции, т.е. фигуры, заключённой между прямыми Функция Если функция
Основные свойства определённого интеграла: 1. 2. 3. 4.Если 5.Если 6.Если Понятие определённого интеграла тесно связано с понятием неопределённого интеграла (первообразной). Если функция
Следствиями формулы Ньютона-Лейбница являются формулы замены переменной и интегрирования по частям в определённом интеграле. Если функции  Если функция
В формуле замены переменной в определённом интеграле, вообще говоря, не предполагается монотонности функции При вычислении неопределённого интеграла по умолчанию предполагалось, что первообразная находится на тех промежутках, на которых выполняемые преобразования подынтегральной функции являются тождественными. При вычислении же определённого интеграла первообразная находится на заданном отрезке, поэтому здесь уже необходимо следить за тождественностью выполняемых преобразований. 7.181Используя теорему об оценке определённого интеграла, оценить следующие интегралы: а) 7.182Не вычисляя интегралов, определить, какой из интегралов больше: а) 7.183Определить средние значения данных функций в указанных промежутках: а) в) 7.184Объяснить, почему формальное применение формулы Ньютона-Лейбница приводит к неверным результатам: а) 7.185Можно ли в интеграле 7.186Доказать, чтодлянепрерывной на отрезке 2) 7.187Доказать, чтоесли 7.188Доказать справедливость следующих равенств: 1) 3) 7.189Найти наибольшее и наименьшее значения функции В задачах 7.190-7.204 вычислить следующие интегралы: 7.190 а) 7.191 а) 7.192 а) 7.193 а) 7.194 а) 7.195 а) 7.196 а) 7.197 а) 7.198 а) 7.199 а) 7.200 а) 7.201 а) 7.202 а) 7.203 а) 7.204 а) Несобственные интегралы. |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 128. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
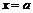 ,
, 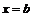 ,
,  и кривой
и кривой 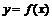 . Число, равное площади криволинейной трапеции, причём площадь той части, которая лежит выше оси
. Число, равное площади криволинейной трапеции, причём площадь той части, которая лежит выше оси 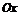 берётся со знаком «+», и ниже её – со знаком «
берётся со знаком «+», и ниже её – со знаком «  » и называется определённым интегралом от функции
» и называется определённым интегралом от функции 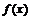 на отрезке
на отрезке 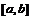 . Определённый интеграл обозначается
. Определённый интеграл обозначается  , где числа
, где числа 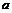 ,
, 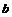 называются нижним и верхним пределами интегрирования.
называются нижним и верхним пределами интегрирования. ,
,  .
.
 .
.  .
. .
.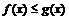 на
на  .
.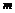 - наименьшее,
- наименьшее, 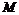 - наибольшее значения
- наибольшее значения  (теорема об оценке определённого интеграла) .
(теорема об оценке определённого интеграла) . такая, что справедливо равенство
такая, что справедливо равенство  (теорема о среднем значении). Число
(теорема о среднем значении). Число  называется при этом средним значением функции
называется при этом средним значением функции  - одна из её первообразных, то справедливо равенство:
- одна из её первообразных, то справедливо равенство: (формула Ньютона-Лейбница).
(формула Ньютона-Лейбница).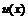 и
и 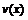 непрерывно дифференцируемы на
непрерывно дифференцируемы на  (формула интегрирования по частям).
(формула интегрирования по частям). - непрерывно дифференцируема на отрезке
- непрерывно дифференцируема на отрезке 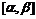 и функция
и функция  , где
, где  ,
,  (
(  -образ отрезка
-образ отрезка 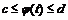 при всех
при всех  ), то
), то (формула замены переменной).
(формула замены переменной). ; б)
; б)  ; в)
; в) 
 или
или  ; б)
; б)  или
или 
 на
на 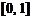 ; б)
; б)  на
на  ;
; на
на  ; г)
; г)  на
на  .
. ; б)
; б) 

 положить
положить  .
. функции
функции 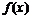 имеем: 1)
имеем: 1)  , если
, если  , если
, если  -непрерывная периодическая функция, определённая при
-непрерывная периодическая функция, определённая при  и имеющая период
и имеющая период  , то
, то  , где
, где  - любое число.
- любое число. ; 2)
; 2)  ;
; ; 4)
; 4) 
 .
. на отрезке
на отрезке 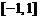 .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 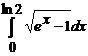 ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 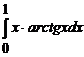 ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в) 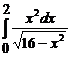 .
.