
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Золотое сечение: арифметика роста ⇐ ПредыдущаяСтр 3 из 3 D Греции золотое сечение обозначали буквой may (ей начиналось греческое слово, в переводе означающее «разрезать» или «делить»), а с начала XX века — буквой фи (Ф) — первой в имени самого прославленного греческого скульптора Фидия (490^30 до н. э.) в знак того, что золотое сечение часто встречается в различных красивых формах. Позднее мы расскажем об использовании Ф в произведениях искусства, включая его относительно узкое применение в главном творении Фидия — афинском Парфеноне (см. с. 124—127). Создание золотого сечения Фи (Ф) — священное число, равное 1,6180339887... Его можно использовать для разделения прямой или прямоугольника на две неравные части, причем отношение двух получившихся частей друг к другу будет таким же, как отношение большей части к целому. Всесторонний подход к вопросу показывает, что деление на это число подобно делению клеток: разделение отрезка в такой пропорции создает другой отрезок, подобный первоначальному. Этот новый отрезок можно считать «ребенком» исходного. Ф позволяет бесконечно продолжать процесс, что может говорить о его участии в воспроизводстве, а следовательно, и в росте. Разделим его точкой Y на отрезки AY и YB. Чтобы эти две части соответствовали золотому сечению, соотношение AY и YB должно быть таким же, как АВ и AY. Оно всегда равно 1.6180339887... к 1. Эта десятичная дробь бесконечна, поэтому в таком виде точно записать ее значение невозможно. Она представляет собой иррациональное число. Иррациональные числа — это числа, которые нельзя передать конечным или периодическим (повторяющимся) набором цифр после десятичной запятой. Еще одно иррациональное число — пи (л -  3,0.. .). Но, будучи иррациональным числом, Ф в отношениях с собой может давать целые рациональные числа. В геометрии это свойство используется при создании многогранников (см. с. 56—57). Многие источники констатируют, что Ф участвует в создании многочисленных жизненных форм в природе. Построение пятиугольника
Алина стороны правильного пятиугольника, вписанного в круг с радиусом 1 ед. = V(10 - 2л/5)/2
Как геометрически построить золотое сечение Чтобы разделить любой отрезок по пропорциям золотого сечения, можно использовать следующий метод треугольников Пифагора. 1. Проведите отрезок АВ. 2. Восстановите из В перпендикуляр ВС. Длина ВС должна составлять половину длины АВ. 3. Проведите отрезок АС. Вы построили прямоугольный треугольник. 4. Поставьте острие циркуля в точку С и проведите дугу радиуса СВ, пересекающую отрезок АС в точке X. 5. Поставьте острие циркуля в точку А и проведите дугу радиуса АХ, пересекающую отрезок АВ в точке V. Точка Y делит отрезок АВ в пропорциях золотого сечения. Некоторые формулы золотого сечения (Ф) Ф = (л/5 + 1)/2 = 1,618 Ф2 = (л/5 + 3)/2 = 2,618 1/Ф = (V5 - 1)/2 = 0,618 Из этого можно заключить, что: Ф2 = Ф + 1 Ф = Ф2 - 1 Ф + Ф2 = Ф' Ф + Ф2 + Ф1 = Ф4 И так далее до бесконечности. Ф = (csc 18°)/2 = 1/(2 sin 18°) = 2 cos 36° = 2/(sec 36°) = 2 sin 54° = 2/(csc 54°) = (sec 72°)/2 = 1/(2 cos 72°) Отсюда ясно, что основные числа - 18, 36, 54 и 72. Поскольку все они произведения 18, это число тесно связано с Ф. Мы уже говорили, что древние люди предпочитали числа, которые можно выразить как целые или дробные числа (2/з> 1/г, 3/4, V9), а еще лучше — дробями, в числителе которых СТОИТ 1 (!/з, Ч6, ■/во). Здесь фи выражено как дробь: Ф = (1 + у/5)12 Можно упростить формулу, разделив все на 2: Ф = 0,5 + 0,5 х V5 Таким образом, Ф полностью выражается через пятерку, поэтому не нужно удивляться тому, что «пятеричность» — это свойство Ф и что Ф наблюдается в пропорциях пятиугольника и пентаграммы. Несоизмеримые числа Однако в десятичной форме фи — бесконечное число. Числа, которые никогда не заканчиваются и не могут быть выражены абсолютно точно, называются несоизмеримыми. Их невозможно построить при помощи базовой геометрии Евклида, циркуля и линейки. Они вызывали любопытство со времен античности. Одна довольно цветистая история повествует, что, когда Гиппас из Метапонтума (кон. VI — нач. V в.) открыл, что золотое сечение невозможно выразить как дробь или отношение двух целых чисел, его собратья-пифагорейцы якобы были настолько шокированы, что принесли в жертву 100 быков. Мне это кажется преувеличением, учитывая, что пифагорейцы были вегетарианцами, но их реакция показывает степень почтения к целым числам и рациональным отношениям, которые выражаются рациональными дробями. Ямвлих из Халкиды (ок. 245—325) утверждал, что пифагорейцы для того, кто открыл несоизмеримые числа, построили гробницу, означавшую, что он должен навсегда удалиться от жизни и пифагорейского братства. Золотой треугольник Золотой, или совершенный, треугольник — это равнобедренный треугольник с углами у основания по 72° и углом при вершине 36°. Разделив пополам углы при основании, мы получаем два — опять-таки золотых! — треугольника. Геометрия пентаграммы
Каждый из треугольников, как CKD на рисунке, является золотым, углы при основании равны 72°, при вершине - 36°. Если считать, что стороны равны 1 ед., основание будет равно 0,618... ед., другими словами, отношение стороны к основанию равно Ф (1,618...).
Золотой треугольник тоже дает золотое сечение 1,618, потому что отношение длинной стороны треугольника к короткой равняется фи, как видно на верхнем рисунке. При помощи этого треугольника можно также получить логарифмическую спираль (см. с. 48-51). Золотая пентаграмма Пентаграмма, или пятиконечная звезда, издавна считается магическим символом. На Западе пентаграмму, направленную одним лучом вверх, часто используют для защиты от зла. Если один луч направлен вниз, пентаграмму считают символом дьявола. Самое известное магическое братство нескольких последних веков — герметический
орден Золотой Зари - разработало Изгоняющий ритуал пентаграммы для рассеивания злых чар. Поэтому неудивительно, что эта ~Ч; фигура обладает особой геометрией. Если внимательно посмотреть | ... на пентаграмму, вы увидите, что она состоит из пяти треугольников, соединенных с перевернута тым правильным пятиугольни- ^ f ком. Если принять длину стороны треугольника за 1 ед., то основание треугольника (или сторона пятиугольника) будет равна 0,618. При этом 1/0,618 = Ф. Другими словами, если разделить длину стороны треугольника на длину основания, получится Ф. Таким образом, правильная пентаграмма состоит из пяти золотых треугольников, соединенных с пятиугольником. Фибоначчи и волшебная последовательность Хотя мировая слава принадлежит Леонардо да Винчи, одно из главных открытий, лежащих в основе современной геометрии, совершил другой Леонардо. В 1202 году Леонардо Пизанский, или Фибоначчи (ок. 1170 — ок. 1240), выпустил «Liber abaci» («Книгу счета»). Там он в 15 главах объяснял основные арифметические действия, в частности, теорию простых чисел, дробей и Евклидову геометрию. А затем, в качестве некой математической забавы, практически случайно, изложил идею числовой последовательности, которой присвоили его имя. Считается, что Леонардо Пизанский принес математическое искусство в Италию из Аравии, т. е. занимался переводами с арабского на латинский язык основных математических работ. Он приобрел их во время многочисленных путешествий в традиционные образовательные центры, включая Египет, Сирию, Грецию, Сицилию и Прованс. Сицилия (как и Толедо) играла особую роль в ознакомлении Запада с арабской наукой. В 827 году остров захватили сарацины, изгнанные норманнскими рыцарями лишь в 1060—1092 годах. В результате во время Леонардо Пизанского там наблюдалось смешение греческой, латинской и арабской культуры и науки. Основа красоты
Леонардо Пизанский первоначально придумал свою последовательность в качестве математического развлечения для подсчета растущей популяции кроликов, которая начинается с одной пары животных. В каждом поколении получалось следующее число кроликов: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... Каждое число является суммой двух предыдущих, поэтому последовательность все время «растет», исходя из предшествующих «родительских» чисел. Эта последовательность кажется самой обычной, если не всматриваться в соотношения двух соседних чисел. Если разделить каждое число на предшествующее, то (округляя до тысячных долей) получится: 3:2 = 1,500 5:3 = 1,666 8:5 = 1,600 13:8 = 1,625 21 : 13 = 1,615 34:21 = 1,619 55:34 = 1,617 89:55 = 1,618 Последующие результаты слегка колеблются в обе стороны, но потом останавливаются на 1,6180339887... Это магическое число передается греческой буквой фи — Ф (см. с. 34). Оно, несомненно, является частью базовой структуры Вселенной и потому может по праву называться священным.
Глава 2
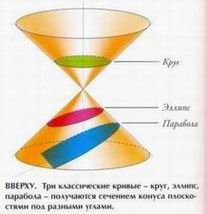
Сначала мы рассмотрим основные фигуры (круг и четыре вида треугольников), а потом три классические геометрические задачи: квадратуру круга, удвоение куба и трисекцию утла. Из всех существующих трехмерных тел только пять (тела Платона) считаются совершенными и еще 13 (связанных с именем Архимеда) — важными. Кроме того, греки также открыли удивительные свойства конуса и рассчитали ряд кривых (включая логарифмическую кривую), которые играют большую роль в геометрии жизни. Греческие геометры построили геометрические фигуры, воплощавшие иррациональные числа, которые вызывали ужас и считались несовершенными. Эти числа, особенно квадратные корни из 2, 3 и 5, играли важную роль в священной геометрии, потому что часто выражали длину диагоналей квадратов и треугольников, построенных в небольших целых числах. Евклид — отец геометрии
С амая известная книга в истории геометрии, да и всей математики, — «Начала» («Элементы») Евклида. В Европе только Библия была продана в большем количестве экземпляров, пока в XX веке не появились такие бестселлеры, как «Властелин колец», «Код да Винчи» и цикл книг о приключениях Гарри Поттера. Вероятно, изучать математику Евклид начал в Афинах с учениками Платона. Он написал десятки книг по различным темам — музыке, математике, оптике, но до нас дошли лишь четыре. «Оптика» содержит одно из первых исследований перспективы (см. с. 142—143). В IV веке Теон Александрийский написал исправленную версию «Начал», которая легла в основу всех переводов вплоть до XIX века, когда в библиотеке Ватикана был найден другой текст. В Средневековье «Начала» не меньше трех раз переводились на арабский. Английский монах-бенедиктинец Аделард Батский (ок. 1070-1 145), путешествовавший по Испании под видом студента-мусульманина, обнаружил арабский текст «Начал» и к 1120 году закончил его перевод на латынь. Этот перевод стал фундаментом всех европейских изданий до XVI века. В 1570 году Генри Биллингсли перевел «Начала» на английский. Джон Ди (см. с. 93—95) написал предисловие к переводу и отметил, что знание основ Евклида способствует изучению оптики, строительства и архитектуры. Великие греческие геометры Древние греки искали красивые решения геометрических задач ради чистого результата. Их геометрия включала расчеты гармонии, которые и составляют священную геометрию, а их последовательная логика стала основой современного научного мышления. Греки создали представления о классической красоте (особенно в скульптуре), потрясающую архитектуру (через греческое и римское Возрождение) и логический научный подход к решению проблем. Эти представления о красоте дополнялись знаниями о форме и пропорциях, на которых стоит вся священная геометрия. Евклид систематизировал геометрию, а Пифагор говорил о святости чисел. Греческие геометры участвовали в разработке теории архитектуры, астрономии, механики и оптики. Их работа по сей день лежит в основании всей западной науки. «Начала» Евклида 13 книг «Начал» содержат основы античной математики. В них входит практически все, что нам известно об элементарной геометрии и многое из геометрии сфер, конусов и других обьемных тел. Для Евклидовой геометрии нужны только циркуль и линейка, причем деления на ней не обязательны, потому что теоремы Евклида выполняются независимо от размеров. Приведенный список книг «Начал» поможет определить источник наиболее важных теорем и кониепиий Евклида. Книги I-IV касаются геометрии плоскости, которую изучают в школе и которая известна как Евклидова геометрия. В книгах I, II и IV рассказывается о прямых и фигурах на плоскости, а III по- свяшена свойствам круга. Книга V- обширный труд о пропорции, основу которого заложил Евдокс Книдский. Эта книга имеет большое значение в изучении священной геометрии. В книге VI изложено учение о подобии. Книги VII-IX рассматривают теорию чисел и основы арифметики. Книга VII посвяшена теории чисел как таковой. Книга X посвяшена иррациональным числам и опирается в основном на работу Теэтета Афинского. Книга XI - основы геометрии твердых тел. Книга XII доказывает теорему о плошади круга. Опирается на работы Евдокса. Книга XIII приводит построение пяти тел Платона. Опирается на работу Теэтета. Эта книга тоже имеет большое значение для священной геометрии.
Фалес Милетский (624—546 до н. э.) Фалес одним из первых привез в Грецию науку геометрию из Египта — за три века до Евклида. Его иногда называют «отцом дедуктивного мышления». Платон (427—347 до н. э.) В 387 году до н. э. Платон основал Академию, которая просуществовала до 529 года. Диалог Платона «Федон» поддерживал теории Пифагора, доказывая, что числа и фигуры - совершенные ноуменальные формы, стоящие за воплощенной реальностью. Теэтет Афинский (417—369 до н. э.) Создатель геометрии пяти тел Платона (см. с. 54—55). Его работа была популярна в эпоху Возрождения среди ученых, занимавшихся пропорциями и священной геометрией. Евдокс Книдский (408—355 до н. э.) Его работа касается пропорций и гармонии — основных элементов греческой архитектуры и священной геометрии. Она изложена в 5-й книге «Начал» Евклида. Евдокс открыл способ определения площади круга и объема пирамиды и конуса.
Менехм (380—320 до н. э.) Первым открыл, что эллипсы, гиперболы и параболы можно получить с помощью конических сечений. Рассчитывая эллиптические орбиты планет, Кеплер опирался на работу Менехма (см. с. 78-79). Архимед (ок. 287—212 до н. э.) Формализовал геометрию простых механизмов. Изучал логарифмические кривые (см. с. 48—51). Архимед открыл 13 полуправильных трехмерных тел (см. с. 56—57). Аполлоний Пергский (262-190 до н. э.) Рассчитал значение числа пи точнее, чем Архимед. Главный вклад Аполлония в геометрию - определение центра кривизны и эволюты эллипса, параболы (см. с. 48-51) и гиперболы. Гиппарх Родосский (190—120 до н. э.) Опубликовал первые тригонометрические таблицы; может быть, изобрел тригонометрию как таковую. Любопытно отметить, что таблицы были основаны на делении крута на 360 градусов (впервые), а каждого градуса — на 60
минут. Эта идея заимствована у вавилонских ученых. Герои Александрийский (10—75) Герон изучал как фигуры на плоскости, так и поверхности объемных тел. Он занимался способами деления областей и объемов в заданной пропорции, что включало, в частности, вычисление кубического корня числа. Менелай Александрийский (70-130) Применил сферическую геометрию в астрономии и тем заложил основы сложных астрономических вычислений. Клавдий Птолемей (85—165) Написал «Альмагест» (в 13 книгах), который считался основным астрономическим трудом, пока теории Птолемея не опровергли Коперник и Кеплер (см. с. 75—79). Математически рассмотрел геоцентрическую теорию движения планет. Папп Александрийский (290—350) Папп работал с пропорциями, геометрическими парадоксами, квадратрисой, трисекцией, сотами, полуправильными телами, минимальной поверхностью, астрономией и механикой. Он также заложил основы современной проективной геометрии, которая используется в картографии. Гипатия Ахександрийская (370—415) Дочь Теона Александрийского, Гипатия воплощала связь философии и геометрии. Она выпустила исправленный вариант «Начал» Евклида и около 400 года возглавила последнюю школу платоников в Александрии.
Основной геометрическим элемент — точка. Две точки определяют прямую. Кривые линии образуют окружности, эллипсы и параболы.
Угол прямой линии равен 1 80°. Три пересекающиеся прямые образуют трехстороннюю фигуру, которая является, наверное, самой устойчивой в геометрии. На этом основан метод триангуляции и измерения земли в картографии. Устойчивость треугольника объясняется тем, что сумма его внутренних углов всегда равна 180° — полукругу. Прямоугольные треугольники Прямоугольный треугольник характеризуется прежде всего тем, что один его угол равен 90°. Остальные два угла могут принимать любые значения (даже 1° и 89°), но сумма трех углов всегда будет равна 180°. Три стороны такого треугольника связаны теоремой Пифагора (см. с. 17). Без прямоугольного треуголь ника не обойтись при постройке зданий и измерении земли. Отдельный случай — прямоугольный треугольник со сторонами 3, 4, 5, который древние египтяне использовали при закладывании полей.
Другой пример — так называемый треугольник Великой пирамиды (см. с. 117-119), стороны которого равны 1, VO (1,273...) и Ф (1,618...). Равносторонние треугольники Следующий важный вид треугольников - равносторонний, все стороны которого одинаковой длины, а все углы равны 60° при любой длине сторон. Шесть соприкасающихся равносторонних треугольников вписываются в окружность (6 х 60° = 360°) и образуют правильный шестиугольник. Равнобедренные треугольники У равнобедренных треугольников равны два угла и длины двух сторон, прилежащих к этим углам. Частный случай — золотой треугольник (см. с. 36—37) с углами 72°, 72° и 36°.
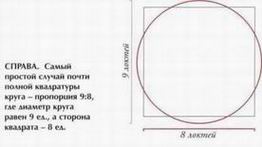
квадратура круга Эта задача возникла из необходимости вычислить площадь круга. В качестве решения было необходимо найти формулу или геометрическое построение, позволяющее быстро построить квадрат, площадь которого будет точно соответствовать площади искомого круга. Это довольно сложная задача, поэтому понятием «квадратура круга» стали обозначать нечто мистическое и почти невозможное. Древние египтяне нашли определенные пары целых чисел (чаще всего упоминаются 8 и 9), которые очень близки к квадратуре круга. Площадь круга диаметром 9 ед. приближенно равна площади квадрата со стороной 8 ед.: Площадь круга = л г = 22/7 х 4,5 х 45 = 63,64 ед.2 Площадь квадрата = 8 х 8 = 64 ед.2 Довольно точно, но все же есть расхождение в 0,56%. Соотношение 8:9 очень интересно, потому что оно соответствует второй ноте гаммы — ре (см. с. 22-23). В 1872 году немецкий математик Фердинанд фон Линдеман (1852—1939) доказал, что л — трансцендентное число. Это окончательно подтвердило невозможность найти квадратуру круга, используя только циркуль и линейку. Еще одно близкое значение можно получить, построив квадрат со стороной 3,14164. Это число получено из: 6 (1 + Ф) / 5 = 3,141640. Этот очень любопытный пример показывает существование почти точной связи между л (3,1415926...) и Ф (золотым сечением, 1,618...). Удвоение куба Вторая задача — построить куб, объем которого был бы ровно в два раза больше заданного. Сначала может показаться, что достаточно удвоить длину каждого ребра, но это даст объем в 2 х 2 х 2 = 8 раз больше первоначального. Для решения необходимо использовать кубические корни, которые в силу их природы невозможно построить только при помощи Евклидовой геометрии. Эта задача тоже имеет практическое значение, потому что связана с созданием стандартных мерных сосудов для жидкостей и зерна. Она применялась и при постройке Парфенона, объем которого в два раза превышал объем первоначального храма (см.
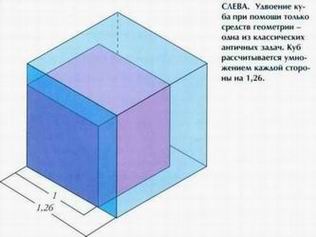
Эту задачу можно решить алгебраически. Если длина стороны первоначального куба равна S, его объем составляет S'. Следовательно, в два раза больший объем куба равен 2S3. А сторона такого куба будет равна V^(2S’) = SV2 = S х 1,26. Трисекция утла Третья задача — разделение угла на три равные части без помощи транспортира. Некоторые углы — например, 135° или 90° — можно разделить на три при помощи циркуля и линейки, но таких углов очень немного. Квадратриса
Греческий философ Гиппий Элидский (ок. 460 - ок. 400 до н. э.) нашел самое точное решение двух из этих трех геометрических задач, когда открыл кривую, названную им квадратрисой.Она строится в квадрате (см. рис. ABCD). Пусть отрезок AD равномерно вращается по часовой стрелке вокруг точки А. Точка D при этом опускается вниз по кривой DFB, пока не совместится с точкой В. DFB образует часть окружности. Пусть одновременно горизонтальная линия (обозначена пунктиром) с той же скоростью опускается из DC в АВ. Точка пересечения горизонтальной линии с врашаюшимся отрезком AD будет перемешаться по кривой DXYG. Эта линия DXVG и есть квадратриса. Ее формула: у = х ctg (х/г х л/2) (г = AD). Рассмотрим прямой угол DAB. Чтобы решить задачу трисекиии угла, проведем пунктирную линию на трети от высоты квадрата. Проведя отрезок из А в точку пересечения этой пунктирной линии с квадратрисой, мы получим угол, равный трети угла DAB. Затем проведем пунктирную линию на двух третях от высоты квадрата, и угол DAY будет равен двум третям угла DAB (углы отсчитываются от перпендикуляра AD). Чтобы построить угол BAZ, равный одной шестой угла DAB, используйте пунктирную линию на одной шестой от высоты квадрата (см. правый рисунок). При помоши квадратрисы можно получить и почти точную квадратуру круга.
поэт Дилан Томас. Логарифмические спирали Существует множест во видов спиралей: плоские, трехмерные, правосторонние, левосторонние, равноугольные, геометрические, логарифмические и прямоугольные. Трехмерные, или объемные, спирали получаются, когда спираль проходит вокруг другого геометрического тела — конуса или цилиндра, создавая винтовые линии, подобные молекуле ДНК (см. с. 72-73). Логарифмическая, или равноугольная, спираль получается, когда в качестве базового числа используется фи (золотое сечение). Логарифмическая спираль строится при помощи «вращающихся квадратов», увеличивающихся из центра вовне в ^«-управляемой гармонической прогрессии (см. с. 49). Логарифмическая спираль - единственная кривая, которая по мере роста не меняет форму. Позднее логарифмическими спиралями занимались основатель логики Рене Декарт (1596—1650) и Якоб Бернулли (1654-1705). Бернулли был настолько восхищен свойствами логарифмической спирали, что попросил нанести ее на свое надгробие со словами Eadem mutata resurgo («Восстану преображенным»). Классические кривые Самая главная кривая - это окружность, но существуют и другие классические кривые, которые знали и которыми пользовались наши предки. Некоторые из них еще только ожидают своего признания как неотъемлемые части природы и священной геометрии. Парабола Парабола — кривая, обладающая интереснейшими качествами. Комната со стенами, имеющими с двух сторон форму параболы, будет пе-
Построение
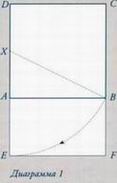
1. Постройте квадрат ABCD со стороной 1 ед. (неважно, в дюймах, сантиметрах или в других единицах). Середину отрезка DA обозначьте X (см. диаграмму 1). 2. 3. Если теперь провести диагонали BE и DF, они будут пересекаться под прямым углом (см. диаграмму 2). Поэтому полученная таким образом логарифмическая спираль называется прямоугольной. 4. HFCG, IJCG, IKLG, IKMN и РКМО соответственно (диаграмма 3). 5. Наконец, проведите плавную кривую, соединяющую внешние углы последовательно добавленных квадратов. Квадраты «врашаются» наружу, сохраняя пропорции золотого сечения (диаграмма 3). редавать звук шепота из фокуса одной параболы в фокус другой даже при наличии прочих шумов. Такая комната существует, например, в Эксплорагори- уме в Сан-Франциско (Калифорния, США). Эллипс Эллипс интересен тем, что его форму имеют орбиты планет, вращающихся вокруг Солнца. Эллипс был известен еще греческим геометрам, но первым применил его к движению планет Иоганн Кеплер (1571 — 1630). Гиппократова луночка Гиппократова луночка — фигура, образованная двумя пересекающимися окружностями с разным радиусом. Гиппократ Хиосский (460—380 до н. э.) рассматривал луночки как возможное средство нахождения квадратуры круга (но безуспешно) (см. с. 46).
Эвольвента Естественная кривая. Ее можно увидеть, например, в изгибе клюва орла, спинном плавнике акулы, кончиках пальмовых листьев. Циклоида Циклоида — это кривая, которую описывает точка на поверхности цилиндра, катящегося по ровной поверхности. Она известна с давних времен: ее используют при строительстве арок и других сооружений. В XVII веке магия циклоиды покоряла математиков и философов, включая Галилея, Паскаля, Декарта, Лейбница и Ньютона. Из-за красоты ее называли «Еленой геометрии». Очень интересны свойства циклоиды: • Длина циклоиды составляет ровно четыре диаметра круга, которым она создана, — очень рациональное число. • • • Циклоида — очень рациональная фигура, получаемая при помощи круга, размеры которого иррациональны (потому что пи — иррациональное число). Конхоида
Евклидова геометрия прямых, — об удвоении куба и трисекции угла (см. с. 46—47). Конхоида имеет форму раковины и образуется взаимодействием фиксированной (базовой) прямой и фиксированной точки (полюса). Обозначим полюс Р и проведем из него пучок лучей так, чтобы они пересекали базовую линию, b — расстояние между Р и линией.
Задолго до нашей эры треугольники использовались для измерения земли — этот метод называется триангуляцией и применяется по сей день. Он основан на том, что на большой территории трудно разметить точный прямоугольник — из-за ошибок при построении углов часто получается параллелограмм. Треугольник гораздо надежней, потому что проводят только одну сторону, а две другие сходятся в точке. Если при этом пользоваться тремя отрезками веревки с узлами (как поступали в Древнем Египте), то можно быстро и практически без ошибок построить треугольник от базовой линии. Разметить прямоугольный треугольник несколько сложнее. Потом из двух таких треугольников вы можете составить идеальный прямоугольник, что очень важно, если вы хотите точно измерить землю и избежать бесконечных территориальных споров. Египтянам приходилось ежегодно повторять измерения земли — после каждого разлива Нила вода уничтожала разметку. Поэтому они достигли в этом совершенства. Египтяне задолго до Пифагора знали, что треугольники со сторонами определенной длины (3,4 и 5 или 17, 144, 145) всегда будуг прямоугольными. Эти особые целые числа позднее были названы тройками Пифагора. Мерные веревки египтян были завязаны таким образом, чтобы давать стороны треугольников, длина которых составляла тройки Пифагора. Конечно, не у всех треугольников такие удобные размеры. Прямоугольные треугольники, образованные не тройками Пифагора, всегда имеют иррациональную гипотенузу (длинную сторону). Вычисление гипотенузы Рассмотрим несколько простых примеров по вычислению гипотенузы с помощью теоремы Пифагора (см. с. 17).
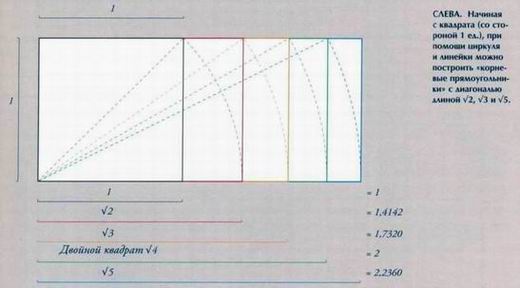
Таким образом, прямоугольные треугольники или состоят из троек Пифагора, или дают иррациональные числа. Поэтому такие «иррациональные числа» и были важны. Древние египтяне нашли геометрический способ получать их, используя «корневые прямоугольники».
Построение «корневых прямоугольников» Начнем с самой простой фигуры - квадрата со стороной 1 ед. Неважно, чему равна единица измерения - дюйму, локтю, метру или даже километру. 1. Проведите диагональ. Получится два прямоугольных треугольника. При помощи теоремы Пифагора найдем длину гипотенузы и таким образом получим первое иррациональное число. Гипотенуза2 = катет I2 + катет 22 Гипотенуза2 = 12 + 12 Гипотенуза2 =1+1=2 Следовательно, гипотенуза = V2 2. Теперь поставим ножку циркуля в начало диагонали и отмерим ее длину. Проведем дугу. 3. Продлим стороны квадрата и получим прямоугольник (красный - см. рис. внизу). Проведем его диагональ - она будет равна V3. Таким образом, мы получаем второе иррациональное число. 4. Повторяйте процесс сколько угодно, каждый раз проводя новую диагональ. Вы получите V4, или двойной квадрат, V5 и т. д. Конечно, V4 - не иррациональное число, оно равно 2, что и дает двойной квадрат. Так наши предки получали иррациональные числа. Очевидно, что они «иррациональны» только при использовании десятичной системы. Геометрически они намного понятней: по сути, это диагонали столь просто построенных прямоугольников.
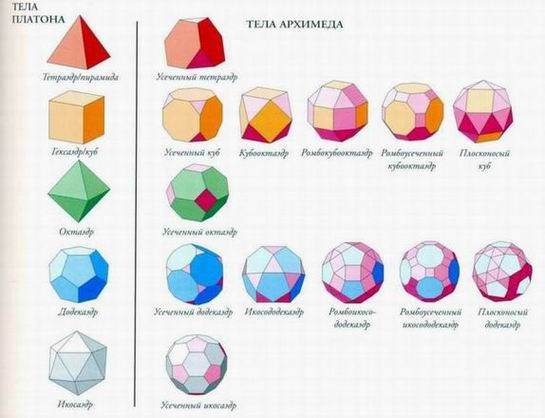
їлатон выделял пять твердых тел, которые считал совершенными: Тетраэдр Четырехгранник (тетра = 4) Гексаэдр/Куб Шестигранник (гекса = 6) Октаэдр Восьмигранник (окта = 8) Додекаэдр Двенадцатигранник (додека = 12) Икосаэдр Двадцатигранник (икоса = 20). Эти пять тел стали важной частью и практической, и священной геометрии, хотя Платон не первым заговорил о них. Первые три — детища Пифагора, в последние два — Теэтета. Миллионы тел состоят из неправильных многогранников, но только пять - из правильных. Из их малочисленности Платон и Аристотель сделали вывод, что они образуют базовые элементы материи и соотнесли пять твердых тел с четырьмя классическими стихиями плюс эфир. «Эдр» означает просто «поверхность», поэтому многогранники, полиэдры, - это трехмерные объекты, поверхности которых являются симметричными многоугольниками (см. табл. ниже). Параметры многогранников связаны друг с другом простым соотношением (теорема Эйлера): Количество ребер + 2 = количество граней + количество вершин
Тела могут показаться на вид сложными, но на самом деле все довольно просто: • • Тетраэдр — пирамида с треугольным основанием. • Октаэдр - две одинаковые пирамиды с квадратным основанием, соединенные вместе. Пять тел соответствуют двум парам стихий («дуалов») и эфиру. Куб (земля) и октаэдр (воздух) — геометрические «дуалы», т. е. один можно построить внутри другого, соединив центры всех граней. Таким образом, можно создать куб в октаэдре внутри куба в октаэдре и т. д., до бесконечности.
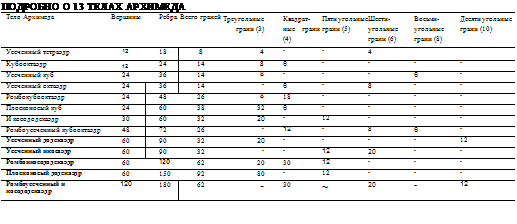
Тел Архимеда Пять тел Платона — «чистые», они состоят из одинаковых многоугольников. Архимед описал 13 дополнительных тел, которые включают два или больше типов многоугольников.
Подлинные труды Архимеда по этой теме до нас не дошли. В эпоху Возрождения все тела, кроме одного, были постепенно открыты заново. И наконец Иоганн Кеплер в поисках священных чисел, лежащих в основе планетарных орбит (см. с. 78-79), восстановил весь набор. Каждая грань любого из 13 тел Архимеда представляет собой симметричный правильный многоугольник. Все многогранники состоят из геометрических фигур Евклида. У каждой вершины тела сходятся одни и те же многоугольники в одной и той же последовательности. Например, к каждой вершине усеченного тетраэдра сходится последовательность шестиугольник—треугольник—шестиугольник. Чтобы дать исчерпывающую оценку этим телам, необходимо рассмотреть взаимосвязь между числом их вершин, ребер и граней (см. табл. внизу). Грани разделены по количеству сторон. Если считать их по вершинам, начинает прослеживаться четкая структура: количество вершин является кратным 12, за исключением икосододекаэдра. 13 тел описываются по типам многоугольников, сходящихся к каждой вершине, — этого достаточно, чтобы их различать. Например, у каждой из 24 вершин усеченного гексаэдра (или усеченного куба) сходятся треугольник (три стороны), восьмиугольник (восемь) и еще один восьмиугольник (снова восемь) - поэтому его можно определять как 3, 8, 8. Однако необходимо обращать внимание и на порядок чисел, описывающих многогранники, особенно когда у вершины сходится больше грех граней.
Как они строятся Семь из 13 тел Архимеда можно получить усечением одного из тел Платона. Усечение — это срезание углов существующего тела, что дает новую грань вместо каждой прежней вершины. Например, квадратная грань (четыре ребра) заменяется восьмиугольной (восемь ребер) — вместо квадратов получаются восьмиугольники. Два архимедовых тела (ромбоикосо- додекаэдр и ромбокубооктаэдр) можно получить противоположным процессом — расширением Платонова тела, поэтому они в каком-то смысле тоже производные от пяти основных тел Платона. Оставшиеся два тела (плосконосый куб и плосконосый додекаэдр) можно получить смещением граней куба и додекаэдра наружу с легким поворотом. При этом каждый многоугольник обрамляется равносторонними треугольниками (например, при получении из куба плосконосого куба).
Свойства фракталов
Фрактальная геометрия приводит к убедительным изображениям феномена естественного роста — береговая линия, листья папоротника, кора деревьев. Они также могут возникать под воздействием климата и вследствие человеческой деятельности — в виде графиков биржевых цен и экономических прогнозов, которые являются самоподобными. Некоторые папоротники — классические примеры природных фракталов: каждая их секция (листочек) — миниатюрная копия всего листа. При увеличение такой листочек выглядит как целый лист. Кроме того, у некоторых видов почки распускаются по логарифмической спирали. Эго означает, что природе не приходится изменять лист на каждой стадии роста, она продолжает повторять изначальную форму. Часто остается незамеченным тот факт, что природные фракталы, в отличие от математически построенных, имеют конец. Фрактал, который описывает карту побережья Великобритании, можно исследовать все в большем и большем увеличении, пока вы не достигнете, скажем, песчинок на берегу. Но вы не сможете дальше уменьшать шкалу, как бывает с чисто математическим фракталом. Важное свойство фракталов — масштабная инвариантность.
|
 Если строить пятиугольник не с помощью циркуля, а благодаря измерениям, то используется формула:
Если строить пятиугольник не с помощью циркуля, а благодаря измерениям, то используется формула: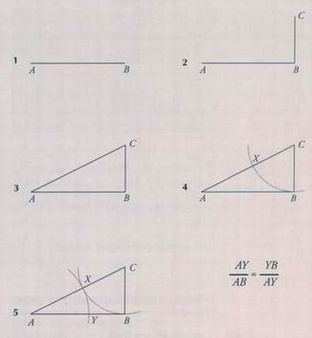 СПРАВА. Палаиио Строиии (Флоренция, 1489), созданный Аеонолл Батиста Альберти, имеет один из самых строгих геометрических планов, подчиняющихся канону архитектурных пропорций XV века.
СПРАВА. Палаиио Строиии (Флоренция, 1489), созданный Аеонолл Батиста Альберти, имеет один из самых строгих геометрических планов, подчиняющихся канону архитектурных пропорций XV века.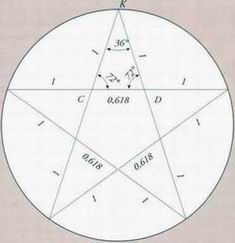 Правильная пентаграмма, вписанная в круг, состоит из перевернутого пятиугольника и пяти треугольников.
Правильная пентаграмма, вписанная в круг, состоит из перевернутого пятиугольника и пяти треугольников.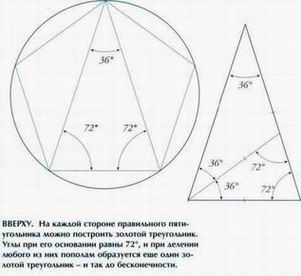 Это действие можно повторять до бесконечности, каждый раз получая новые золотые треугольники.
Это действие можно повторять до бесконечности, каждый раз получая новые золотые треугольники.

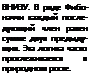
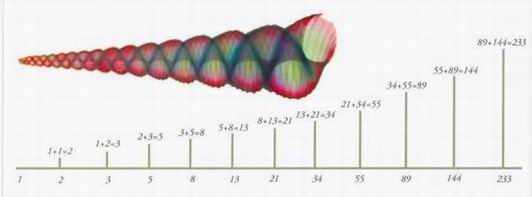
 Дэн Браун использует числа Фибоначчи в самом начале книги «Код да Винчи»: эту последовательность пишет на полу умирающий куратор Соньер, а потом она используется как пароль к банковской ячейке.
Дэн Браун использует числа Фибоначчи в самом начале книги «Код да Винчи»: эту последовательность пишет на полу умирающий куратор Соньер, а потом она используется как пароль к банковской ячейке. Архитекторы Древней Греции и эпохи Возрождения эффективно использовали фи для создания приятных глазу пропорций здания, иногда вплоть до размеров дверей и окон. Достаточно сравнить постройки этих периодов с, допустим, современными сооружениями 1960-х годов, характеризующимися произвольными, «социально ориентированными» размерами, и станет понятно, что Ф — не просто математическая концепция, а часть основ красоты.
Архитекторы Древней Греции и эпохи Возрождения эффективно использовали фи для создания приятных глазу пропорций здания, иногда вплоть до размеров дверей и окон. Достаточно сравнить постройки этих периодов с, допустим, современными сооружениями 1960-х годов, характеризующимися произвольными, «социально ориентированными» размерами, и станет понятно, что Ф — не просто математическая концепция, а часть основ красоты. Греческие геометры, величайшим из которых был Евклид, рассматривали совершенство геометрии как отражение разума Творца. Чтобы максимально отделить ее от физического мира, для начертания и доказательства теорем они использовали только прямую направляющую (линейку без делений) и циркуль.
Греческие геометры, величайшим из которых был Евклид, рассматривали совершенство геометрии как отражение разума Творца. Чтобы максимально отделить ее от физического мира, для начертания и доказательства теорем они использовали только прямую направляющую (линейку без делений) и циркуль.






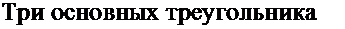
 о<
о< Две прямые линии дают угол, который измеряется в градусах и минутах по шестидесятеричной системе, изобретенной в Вавилоне много тысяч лет назад. Она намного лучше подходит для работы с дробями, чем современная десятеричная система. Вавилоняне разделили круг на 360 градусов, каждый градус — на 60 минут, а каждую минуту — на 60 секунд. Благодаря своей системе счета они могли с высокой точностью записывать иррациональные числа (например, у/2 - с точностью до восьмого знака).
Две прямые линии дают угол, который измеряется в градусах и минутах по шестидесятеричной системе, изобретенной в Вавилоне много тысяч лет назад. Она намного лучше подходит для работы с дробями, чем современная десятеричная система. Вавилоняне разделили круг на 360 градусов, каждый градус — на 60 минут, а каждую минуту — на 60 секунд. Благодаря своей системе счета они могли с высокой точностью записывать иррациональные числа (например, у/2 - с точностью до восьмого знака).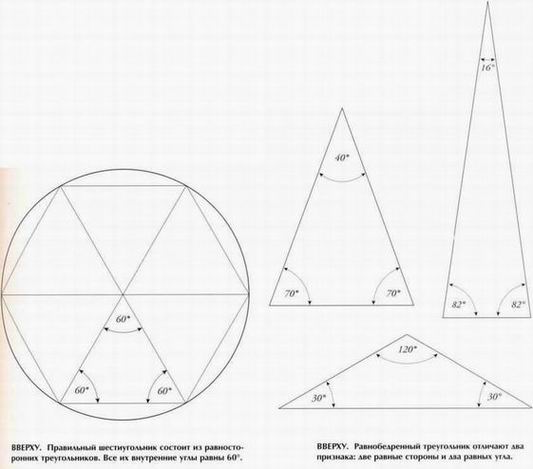 Они брали веревку с 12 узлами, завязанными через равные промежутки, и, натягивая ее, получали прямоугольный треугольник со сторонами 3, 4 и 5 ед.
Они брали веревку с 12 узлами, завязанными через равные промежутки, и, натягивая ее, получали прямоугольный треугольник со сторонами 3, 4 и 5 ед.
 с. 124-127).
с. 124-127).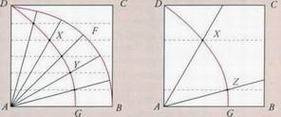

 логарифмической спирали
логарифмической спирали Поставьте ножку циркуля в точку X и начертите окружность радиусом ВХ. Пересечение окружности с прямой, которой принадлежит отрезок DA, обозначьте Е. Из точки Е постройте новый прямоугольник EFBA (см. диаграмму 1). Таким образом, мы получаем золотой прямоугольник EFCD и приходим к нескольким «волшебным» результатам. Например, отрезок DE делится точкой А в пропорции золотого сечения.
Поставьте ножку циркуля в точку X и начертите окружность радиусом ВХ. Пересечение окружности с прямой, которой принадлежит отрезок DA, обозначьте Е. Из точки Е постройте новый прямоугольник EFBA (см. диаграмму 1). Таким образом, мы получаем золотой прямоугольник EFCD и приходим к нескольким «волшебным» результатам. Например, отрезок DE делится точкой А в пропорции золотого сечения.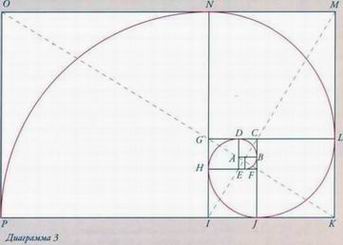 Теперь возьмите длинную сторону золотого прямоугольника, DE, и постройте квадрат HEDG. Продолжайте строить квадраты, каждый раз пользуясь длинной стороной полученного золотого прямоугольника - HF, )С, LG и N1, чтобы создавать новые золотые прямоугольники,
Теперь возьмите длинную сторону золотого прямоугольника, DE, и постройте квадрат HEDG. Продолжайте строить квадраты, каждый раз пользуясь длинной стороной полученного золотого прямоугольника - HF, )С, LG и N1, чтобы создавать новые золотые прямоугольники,

 Площадь под дугой арки любой циклоиды равна точно трем площадям круга, вращением которого она образуется.
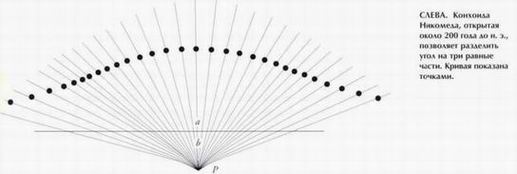
Площадь под дугой арки любой циклоиды равна точно трем площадям круга, вращением которого она образуется.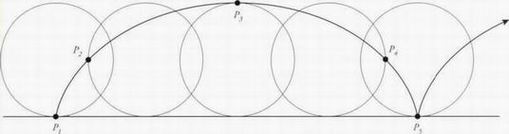 Говорят, что греческий математик Нико- мед (3—2 вв. до н. э.) открыл конхоиду и использовал ее для решения двух классических задач, которые не могла решить
Говорят, что греческий математик Нико- мед (3—2 вв. до н. э.) открыл конхоиду и использовал ее для решения двух классических задач, которые не могла решить При помощи линейки отложите на каждом луче выше линии отрезок длиной а. Конхоида — это кривая, которая соединяет концы этих отрезков.
При помощи линейки отложите на каждом луче выше линии отрезок длиной а. Конхоида — это кривая, которая соединяет концы этих отрезков.


 П
П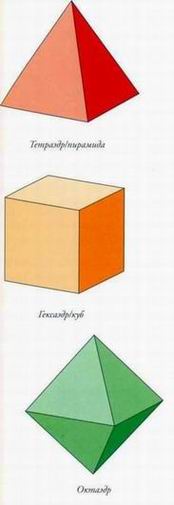 Куб — основная форма коробок.
Куб — основная форма коробок. Аналогично, другие стихии символизируют тетраэдр (огонь) и икосаэдр (вода) — они тоже «дуалы» и тоже строятся друг внутри друга.
Аналогично, другие стихии символизируют тетраэдр (огонь) и икосаэдр (вода) — они тоже «дуалы» и тоже строятся друг внутри друга.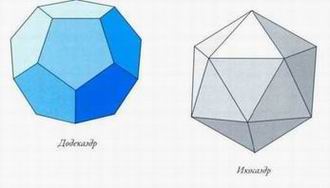 Таким образом, получается полная симметрия между двумя парами стихий: земля—воздух и огонь—вода. Додекаэдр — собственный «дуал», т. е. эфир может самовоспроизводиться.
Таким образом, получается полная симметрия между двумя парами стихий: земля—воздух и огонь—вода. Додекаэдр — собственный «дуал», т. е. эфир может самовоспроизводиться.

 1975 году французский математик Бенуа Мандельброт определил фрактал как объект, каждый фрагмент которого повторяется при любом уменьшении масштаба. Это качество напоминает о фи (золотом сечении), священной пропорции, сохраняющейся при каждом делении отрезка или прямоугольника (см. с. 34—39). На самом деле, и фракталы, и фи имеют отношение к закономерностям природного роста.
1975 году французский математик Бенуа Мандельброт определил фрактал как объект, каждый фрагмент которого повторяется при любом уменьшении масштаба. Это качество напоминает о фи (золотом сечении), священной пропорции, сохраняющейся при каждом делении отрезка или прямоугольника (см. с. 34—39). На самом деле, и фракталы, и фи имеют отношение к закономерностям природного роста. Существует два типа фракталов: геометрический и случайный. Снежинка — геометрический фрактал, который растет путем добавления равносторонних треугольников по особым схемам. Случайные фракталы создаются в процессе компьютерного моделирования.
Существует два типа фракталов: геометрический и случайный. Снежинка — геометрический фрактал, который растет путем добавления равносторонних треугольников по особым схемам. Случайные фракталы создаются в процессе компьютерного моделирования.