Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Скалярное произведение в координатной форме.(формула) ⇐ ПредыдущаяСтр 3 из 3 Если векторы заданы своими координатами
18.Векторное произведение векторов(определение) Векторным произведением вектора 1. 2. 3. Векторное произведение обладает следующими свойствами: 1. 2. 3. 4. Векторное произведение равно нулю (нуль вектору) тогда и только тогда, когда 5. Если 19.Векторное произведение векторов в координатной форме(формула) 20.Смешанное произведение векторов (определение). Смешанным произведением тройки векторов  Таким образом, смешанное произведение векторов Знак произведение положителен, если векторы 21.Смешанное произведение векторов в координатной форме. .
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 197. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  , т.е.
, т.е.  ,
,  , то, перемножая эти векторы скалярно и используя таблицу умножения ортов, получим выражение скалярного произведения
, то, перемножая эти векторы скалярно и используя таблицу умножения ортов, получим выражение скалярного произведения  через координаты векторов:
через координаты векторов:
 на вектор
на вектор  называется вектор
называется вектор  , длина и направление которого определяется условиями:
, длина и направление которого определяется условиями: , где
, где 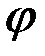 ‑ угол между
‑ угол между  и
и 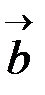 ;
;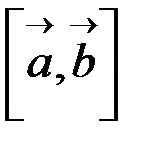 перпендикул каждому из векторов
перпендикул каждому из векторов 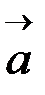 и
и  ;
; направлен так, что кратчайший поворот от
направлен так, что кратчайший поворот от  к
к  виден из его конца совершающимся против часовой стрелки.
виден из его конца совершающимся против часовой стрелки. ;
; ;
; ;
; и
и  коллинеарны. В частности,
коллинеарны. В частности,  для любого вектора
для любого вектора  ;
; и
и  неколлинеарны, то модуль векторного произведения равен площади параллелограмма
неколлинеарны, то модуль векторного произведения равен площади параллелограмма  построенного на этих векторах, как на сторонах.
построенного на этих векторах, как на сторонах.
 и
и  называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора  на векторное произведение
на векторное произведение  . Если рассматриваемые векторы
. Если рассматриваемые векторы  есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор
есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор  , то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов
, то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов  (которое обозначается
(которое обозначается  ) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах
) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах  направлен так, что кратчайший поворот от
направлен так, что кратчайший поворот от  к
к  виден из его конца совершающимся против часовой стрелки.
виден из его конца совершающимся против часовой стрелки.