
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Производная высших порядков.Стр 1 из 3Следующая ⇒ Предел функции по Гейне (на языке последовательности) А называется пределом функции y=f(x) при x→xо , если для любой последовательности допустимых аргументов сходящихся к хо (
Предел функции по Каши (на языке ε- окрестности)А называется пределом функции y=f(x) при x→xо если для любого ε > 0 (сколь угодно малого) найдётся так будет выполняться неравенство (f(x)-A) < 4.Теорема о существовании конечного предела: 5.1-ый замечательный предел:
6.2-ой замечательный предел: 7.Непрерывность функции в точке: Ф-ция y = f(x) называется непрерывной в (.) х0, если: 1. Она определена в этой точке (.) х0 2. Существует 3. y = x2 – непрыв. в (.) x0 1. 2. 3. В (.) x0 = 2 f(x) непрерыв. Ф-ция y = f(x) называется непрерывной в (.) х0, если: 1. б. м преращение аргумент ∆x соответствует 2. она определенна в (.) х0 ; Ф-ция y = f(x) называется непрерывной в (.) х0, если: 1. она определенна в (.) х0 ; 2.
3.
8.Точки разрыва функции Различают 2 вида разрыва ф-ции: Го рода Го рода Если хотя бы одно из условий непрерывности не выполняется, то х0 – (.) разрыва Если (А и В – конечные числа, при чём А Если А = В, то в (.) х0 – устранимый разрыв 1-го рода Если хотя бы один из односторонних пределов не существует или равен 9.Производная – предел отношение преращения ф-ции к преращению аргумента при условии, что последнее стремится к 0.  Производная сложной функции Пусть
Или более кратко Правило можно записать также в виде: 11. Производная функции, заданная параметрически.Теорема: Пусть функция задана параметрически Производная высших порядков. Если функция f(x) , определенная в A , имеет производную во всех точках A , то эту производную можно рассматривать как новую функцию g(x)=f’(x) ,x принадлежит А . К этой функции применимы все предельные законы, в том числе и дифференцирование. Если g(x), определенная в A , имеет конечную производную g’(x) в точке x прин. A , то значение этой производной является второй производной функции f(x) . Аналогично вычисляются производные более высоких порядков. 13.Исследование функции на монотонность. Точки экстремума. Функция Теорема. Если функция Дифференцируемая функция является возрастающей на промежутке Локальный экстремум Точка Точка Точки локального минимума и локального максимума называются точками локального экстремума. Необходимым условием локального экстремума дифференцируемой функции является выполнение равенства Решения этого уравнения называют стационарными точками. Исследование стационарных точек I правило. Если при возрастании II правило. Если вторая производная Точками локального экстремума функции могут быть такие точки, в которых производная не существует или обращается в бесконечность. Исследовать такие точки можно по I правилу. Экстремум в такой точке называется острым экстремумом. Глобальный экстремум.Непрерывная на отрезке · Находят стационарные точки · Находят точки · Вычисляют значения:
Это и будут |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 181. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
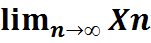 = xo ), соответственно последовательность функций сходится к числу А
= xo ), соответственно последовательность функций сходится к числу А  =A, запис.
=A, запис.  =A
=A такое, что: как только будет выполняться неравенство 0 < (x - xо) <
такое, что: как только будет выполняться неравенство 0 < (x - xо) < 









 б.м преращение ф-ии
б.м преращение ф-ии
 односторонние пределы
односторонние пределы
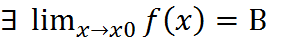
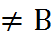 , то в (.) х0 разрыв 1-го рода, в (.) х0 – скачок =
, то в (.) х0 разрыв 1-го рода, в (.) х0 – скачок = 
 то в (.) х0 разрыв 2-го рода.
то в (.) х0 разрыв 2-го рода. и
и  . Тогда можно определить сложную функцию
. Тогда можно определить сложную функцию  . Если функция
. Если функция  дифференцируема в точке
дифференцируема в точке 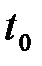 , а функция
, а функция  дифференцируема в точке
дифференцируема в точке  , то сложная функция по правилу цепочки:
, то сложная функция по правилу цепочки: .
. .
. .
. , где функции x(t) и y(t) дифференцируемы. Тогда y’x=
, где функции x(t) и y(t) дифференцируемы. Тогда y’x=  .
. называется возрастающей на промежутке
называется возрастающей на промежутке  , если
, если 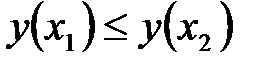 для любых точек
для любых точек  и
и  из промежутка
из промежутка  . Функция называется убывающей на
. Функция называется убывающей на  .
. непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  , то для того, чтобы
, то для того, чтобы 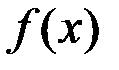 была возрастающей (убывающей) необходимо и достаточно, чтобы
была возрастающей (убывающей) необходимо и достаточно, чтобы 
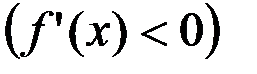 в каждой внутренней точке интервала
в каждой внутренней точке интервала 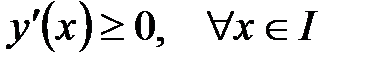
 называется точкой локального максимума функции
называется точкой локального максимума функции  , если существует интервал
, если существует интервал  , содержащий точку
, содержащий точку 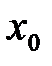 такой что
такой что  .
. .
. . Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение:
. Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение:  при переходе через стационарную точку
при переходе через стационарную точку  производная
производная 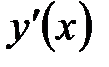 меняет знак с + на ‑ , то
меняет знак с + на ‑ , то  ‑ точка локального минимума функции
‑ точка локального минимума функции  . Если
. Если  не меняет знак в точке
не меняет знак в точке  в стационарной точке
в стационарной точке  функция
функция  принимает свое наибольшее значение
принимает свое наибольшее значение 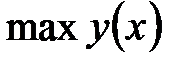 и свое наименьшее значение
и свое наименьшее значение  в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений
в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений  функции;
функции; , в которых производная
, в которых производная  не существует или обращается в бесконечность;
не существует или обращается в бесконечность; ‑ и выбирают среди этих чисел наибольшее и наименьшее.
‑ и выбирают среди этих чисел наибольшее и наименьшее. и
и