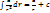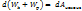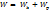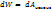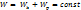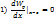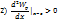Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Кинетическая энергия и ее свойства. Доказательство теоремы о кинетической энергии.
mV^2/2=Wk Wk – кинетическая энергия 1) Wk 2)Wk не зависит от выбора СО 3) Wk = mV^2/2* m/m=(mV)^2/2m=p^2/2m dWk=dA ∆Wk=A mV2^2/2 – mV1^2/2=A Теорема о кинетической энергии Изменение кинетической энергии тела равно работе всех сил, действующих на это тело dA=Fdl=ma*dl*m*dV/dt=mVdV=d(mV^2/2)=dWk Работа как функция процесса. Консервативные силы. Потенциальная энергия. Работа- ф-ия процесса. Зависит от траектории. dA=F*dl A12= Консервативные силы - силы, работа которых не зависит от траектории, по которой движется тело, а зависит от нач и кон точек h1 h1 Работа силы тяжести определ. только положением нач и кон точек траектории Консервативные силы: кулоновские, упругости, меж молек взаимод, гравитационные
A= Wp-потенциальная энергия тела в данном силовом поле (характеризует взаимодействие тела с др телами, с теми телами, которые создают данное силовое поле) A1,2= -∆Wp Работа консервативной силы = убыли потенциальной энергии тела Связь потенциальной энергии с консервативной силой. Примеры: сила тяжести, сила упругости. A= -∆Wp dA=-dWp, // 1) dr=(dx, 0, 0) Fxdx=-dWp Fx= - dWp/dx 2) dr=(0,dy, 0) Fy= - dWp/dy 3) dr=(0,0,dz) Fz= - dWp/dz F=Fxi+Fyj+Fzk= - (
F= - 1)Тело в однородном поле тяжести(тело движ по оси z) F=(0,0,-mg) Fz=-dWp/dz dWp= -Fzdz=mgdz Wp= Wp=mgz 2)сила упругости F=(-kx,0,0) Fупр= dWp/dx dWp=-Fупрdx= kxdx Wp= X=0, Wp=0, 0=0+c c=0 Wp=kx^2/2 F= F ’ =
9. Поле центральных сил. Его потенциальность. Связь центральной силы и потенциальной энергии. Кулоновские поля  F= r/r=er Т.к. сила наз центральной, то и поле центральное. Все центральные силы явл консервативными. А12= r*dr=1/2*d(r*r)=1/2dr^2=rdr Центральная силa не зависит от ее природы Связь центральной силы и потенциальной энергии F= = - ( F= - dWp/dr*r/r=dWp/dr *er Fr= - dWp/dr Кулоновской наз сила, которая изменяется по з-ну обратных квадратов F dWp=-Fr dr= - Wp= - r Wp= Закон сохранения механической энергии. Границы движения частиц в потенциальном поле. Условия устойчивого равновесия.
Изменение полной механической энергии системы равно работе неконсервативных сил, действующих в этой системе.
Закон сохранения механической энергии: Полная механическая энергия системы есть величина постоянная, если в системе не действует неконсервативная сила.
Финитным называется движение частицы в ограниченной области пространства (Пример: Солнеч. система) Инфинитным называется движение, при котором частица может удалятся от начала координат на сколь угодное расстояние. Условия устойчивого равновесия:
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 247. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
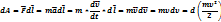
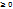

 h2 угол не 90 градусов A=mg(h1-h2)
h2 угол не 90 градусов A=mg(h1-h2)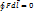 –признак потенциальности поля (консервативности сил)
–признак потенциальности поля (консервативности сил) = -∆Wp
= -∆Wp
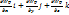 )=-gradWp (grad-сумма производных(показывает направление бысрейшего возрастания функции))
)=-gradWp (grad-сумма производных(показывает направление бысрейшего возрастания функции)) =∂/∂xi+∂/∂yj+∂/∂zk
=∂/∂xi+∂/∂yj+∂/∂zk ∂Wp/∂xi+∂Wp/∂yj+∂Wp/∂zk=gradWp
∂Wp/∂xi+∂Wp/∂yj+∂Wp/∂zk=gradWp Wp
Wp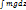 =mgz+C, z=0, Wp=0 0=0+cc=0
=mgz+C, z=0, Wp=0 0=0+cc=0 +c
+c
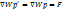
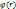 * r/r=
* r/r=  (r)er
(r)er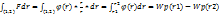
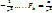
 /r^2 dr
/r^2 dr