
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Зведення задач теорії ігор до задач лінійного програмування ⇐ ПредыдущаяСтр 5 из 5 Розглянемо гру
Відповідно до теореми 3, для оптимальної стратегії першого гравця Розділивши тепер обидві частини останньої нерівності на
Покладемо
Використовуючи введене позначення, перепишемо умову
Так як перший гравець прагне одержати максимальний виграш, то він повинен забезпечити мінімум величині Аналогічні міркування показують, що визначення оптимальної стратегії другого гравця зводиться до знаходження максимального значення функції Таким чином, щоб знайти розв’язок даної гри, обумовленої матрицею Пряма задача: знайти максимальне значення функції
за умов Двоїста задача: знайти мінімальне значення функції за умов Використовуючи розв’язок пари двоїстих задач, одержуємо формули для визначення стратегій і ціни гри:
Отже, процес знаходження розв’язку гри з використанням методів лінійного програмування включає наступні етапи: 1. Складають пари двоїстих задач лінійного програмування, еквівалентних даній матричній грі.  2. Визначають оптимальні плани пари двоїстих задач. 3. Використовуючи співвідношення між планами пари двоїстих задач і оптимальними стратегіями і ціною гри, знаходять розв’язок гри. Приклад 4. Знайти рішення гри, обумовленою матрицею
Рішення. Складемо двоїсту пару задач лінійного програмування: пряма задача: знайти максимум функції за умов
двоїста задача: знайти мінімум функції за умов
Знаходимо оптимальні плани прямої і двоїстої задач Вихідна задача має оптимальний план Оптимальний план двоїстої задачі Отже, ціна гри а оптимальні стратегії гравців:
Вище було показано, що для всякої матричної гри можна записати симетричну пару двоїстих задач. Справедливо і зворотне: для всякої симетричної пари двоїстих задач можна записати матричну гру. Нехай задана симетрична пара двоїстих задач: пряма задача: двоїста задача: Тоді цій симетричній парі двоїстих задач можна поставити у відповідність гру, обумовлену матрицею
Слід зазначити, що якщо кожна матрична гра має оптимальні стратегії, то не всяка задача лінійного програмування має розв’язок. Приклад 5. Побудувати гру, обумовлену наступною парою двоїстих задач:
пряма задача:
двоїста задача:
Рішення.
Отже, вихідній симетричній парі двоїстих задач можна поставити у відповідність матричну гру, обумовлену матрицею
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 208. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , обумовлену матрицею
, обумовлену матрицею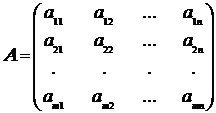 .
. і ціни гри
і ціни гри  виконується нерівність
виконується нерівність  . Припустимо для визначеності, що
. Припустимо для визначеності, що  . Це завжди може бути досягнуте завдяки тому, що додавання до всіх елементів матриці А того самого постійного числа
. Це завжди може бути досягнуте завдяки тому, що додавання до всіх елементів матриці А того самого постійного числа  не приводить до зміни оптимальних стратегій, а тільки лише збільшує ціну гри на
не приводить до зміни оптимальних стратегій, а тільки лише збільшує ціну гри на  .
.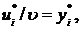 тоді
тоді 
 у виді
у виді .
. . З врахуванням цього, визначення оптимальної стратегії першого гравця зводиться до знаходження мінімального значення функції
. З врахуванням цього, визначення оптимальної стратегії першого гравця зводиться до знаходження мінімального значення функції  при умовах
при умовах 
 при умовах
при умовах  . Тут
. Тут  .
. , потрібно побудувати наступну пару двоїстих задач і знайти їхні розв’язки.
, потрібно побудувати наступну пару двоїстих задач і знайти їхні розв’язки. .
. .
.


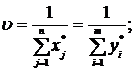
 .
.
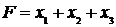
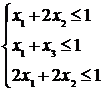




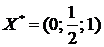 ,
, .
.



 .
. ,
,




 .
.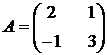 ;
;  ; .
; . 
 .
.