
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Керування дискретними лінійними системами ⇐ ПредыдущаяСтр 3 из 3 Література:[3, c.108-112]. Мета роботи: Застосувати теоретичні критерії дослідження керовності дискретних лінійних систем до розробки алгоритмів розрахунку управління для переведення їх у наперед заданий стан.
Зміст роботи: Дослідити, чи є цілком керовною задана дискретна лінійна система керування. Розрахувати управління для її переведення у наперед заданий стан, використовуючи програмні засоби одного з пакетів Maple, Mathcad чи Matlab.
Методичні вказівки Розглянемо дискретну лінійну систему керування вигляду
де Теорема. Для того, щоб лінійна дискретна система (4.1) була цілком керовною на проміжку від
При цьому керування, яке переводить систему із стану
У випадку стаціонарних дискретних систем керування умова керовності набуде вигляду
Якщо матриця При цьому система (4.3) запишеться так:
Завдання для самостійної роботи Для заданих матриць  Варіанти матриць
Лабораторна робота №5 Оптимальне керування. Принцип максимуму Понтрягіна Література:[5, с. 421-489], [6, с. 13-85]. Мета роботи: Навчитися застосовувати принцип максимуму Понтрягіна до знаходження оптимального керування динамічними системами.
Зміст роботи: Розв’язати запропоновану задачу пошуку оптимального керування, використовуючи принцип максимуму Понтрягіна. Скласти програму для графічного відображення поведінки системи під дією розрахованого керування однією з алгоритмічних мов.
Методичні вказівки Основна задача. Нехай задана динамічна система
. . . . . . . . . . . . . . . . .
або у векторній формі
де Нехай
або у векторній формі
Система (5.3) називається приєднаною до системи (5.1). Функція Гамільтона задач (5.1),(5.2) має вигляд
Тоді динамічна і приєднана системи можуть бути записані через канонічні рівняння
Теорема. Нехай Якщо необхідно мінімізувати двічі диференційовну за всіма аргументами функцію Якщо ставиться задача мінімізації функціоналу
Приклад 5.1. Розв’язання. Умови трансверсальності.Часто у задачі (5.1),(5.2) накладаються умови вигляду Вимагається знайти таке оптимальне керування, яке переводить точку
Приклад 5.2. Розв’язання. Маємо
З умов Аналогічно одержують умови трасверсальності для початкової точки у випадку, коли Завдання для самостійної роботи Розв’язати наведені нижче задачі. Розробити алгоритми і скласти програму для графічного відображення поведінки системи під дією розрахованого керування. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28.
Література 1. Александров А.Г. Оптимальные и адаптивные системы. – М.: Высшая Школа, 1989. – 263 с. 2. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1986. – 544 с. 3.Бублик Б.Н., Кириченко Н.Ф. Основы теории управления. - К.: Вища школа, 1975. - 328 с. 4.Гантмахер Ф.Р. Теория матриц. - М.: Наука, 1967. - 576 с. 5. Васильев Ф.П. Численные методы решения экстремальных задач. – М.: Наука, 1998. – 552 с. 6.Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. – М.: Наука, 1983. – 392 с. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 174. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (4.1)
, (4.1) —
—  -вимірний вектор стану системи в точці
-вимірний вектор стану системи в точці 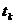 ,
, 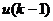 — вектор керування в точці
— вектор керування в точці  ,
, 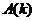 і
і  - деякі матриці, елементи яких залежать від дискретного аргументу
- деякі матриці, елементи яких залежать від дискретного аргументу  до
до  , необхідно і досить, щоб виконувалась умова:
, необхідно і досить, щоб виконувалась умова: (4.2)
(4.2)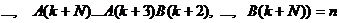 .
. в стан
в стан 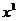 знаходиться як розв’язок системи лінійних алгебраїчних рівнянь
знаходиться як розв’язок системи лінійних алгебраїчних рівнянь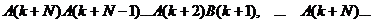
 (4.3)
(4.3)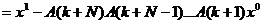 .
. (4.4)
(4.4) у стаціонарній системі складається з одного стовпця, то умова (4.3) зводиться до нерівності
у стаціонарній системі складається з одного стовпця, то умова (4.3) зводиться до нерівності .
.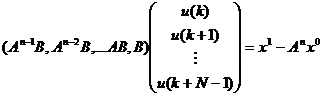 .
. і
і  дискретної стаціонарної лінійної системи керування обчислити керування, яке за п’ять кроків переводить систему із стану з усіма нульовими компонентами у стан з усіма одиничними компонентами. Для проведення відповідних розрахунків можна використати один із пакетів Maple, Mathcad чи Matlab.
дискретної стаціонарної лінійної системи керування обчислити керування, яке за п’ять кроків переводить систему із стану з усіма нульовими компонентами у стан з усіма одиничними компонентами. Для проведення відповідних розрахунків можна використати один із пакетів Maple, Mathcad чи Matlab.
 (5.1)
(5.1)
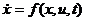 ,
,  з початковою умовою
з початковою умовою 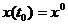 і областю допустимих керувань
і областю допустимих керувань 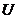 . Тут
. Тут  –
–  мають частинні похідні
мають частинні похідні  (
(  і неперервні разом з цими похідними за сукупністю своїх аргументів. Шукається таке допустиме керування і відповідна траекторія системи (5.1), щоб для фіксованого скінченного моменту часу
і неперервні разом з цими похідними за сукупністю своїх аргументів. Шукається таке допустиме керування і відповідна траекторія системи (5.1), щоб для фіксованого скінченного моменту часу 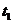 вираз
вираз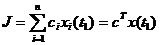 , (5.2)
, (5.2) - задані сталі, був мінімальним.
- задані сталі, був мінімальним. – вектор-функція з компонентами
– вектор-функція з компонентами  , яка є розв’язком задачі
, яка є розв’язком задачі ,
,  ,
,  , (5.3)
, (5.3) ,
,  , де
, де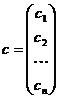 ,
, 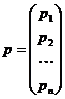 ,
,  .
.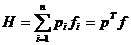 .
. ,
,  ,
,  – розв’язок задачі (5.1),(5.3). Тоді існує функція
– розв’язок задачі (5.1),(5.3). Тоді існує функція  .
. , то в принципі максимуму Понтрягіна початкові умови для приєднаної системи треба замінити на
, то в принципі максимуму Понтрягіна початкові умови для приєднаної системи треба замінити на 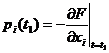 .
. , де функція
, де функція 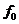 задовольняє ті ж умови, що й
задовольняє ті ж умови, що й 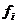 , то функція Гамільтона визначається формулою
, то функція Гамільтона визначається формулою  , а приєднана система має вигляд
, а приєднана система має вигляд ,
,  ,
, 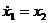 ,
, 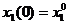
 ,
,  ,
,  ,
, 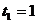 ,
,  .
. ,
, 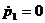 ,
,  ,
,  ,
,  , тобто
, тобто 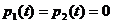 . Звідси
. Звідси  . Максимум
. Максимум  досягається при
досягається при  .
. ,
,  , причому вважається, що функції
, причому вважається, що функції  двічі диференційовні по всіх
двічі диференційовні по всіх  і якобіан
і якобіан  має максимальний ранг
має максимальний ранг  . Тоді умови
. Тоді умови  ,
,  у довільну точку цього многовиду. В цьому випадку кінцеві умови для
у довільну точку цього многовиду. В цьому випадку кінцеві умови для  в принципі максимуму Понтрягіна потрібно замінити умовами трансверсальності
в принципі максимуму Понтрягіна потрібно замінити умовами трансверсальності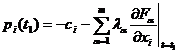 ,
, 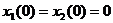 ,
,  ,
, 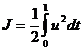 .
. ,
,  ,
, 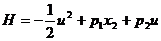 ,
, 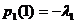 ,
,  , тобто
, тобто  і
і  . Звідси, максимум функції Гамільтона дає оптимальне керування
. Звідси, максимум функції Гамільтона дає оптимальне керування 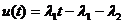 . Невідомі параметри
. Невідомі параметри  і
і  потрібно вибрати так, щоб система переводилась у кінцеву точку
потрібно вибрати так, щоб система переводилась у кінцеву точку  ,
, ,
, 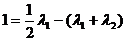 , так що оптимальне керування має вигляд
, так що оптимальне керування має вигляд 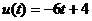 .
. не задано, а лише вимагається, щоб ця точка задовольняла систему
не задано, а лише вимагається, щоб ця точка задовольняла систему  ,
, 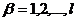 . Тоді для приєднаної вектор-функції має виконуватись умова
. Тоді для приєднаної вектор-функції має виконуватись умова  ,
,  ,
,  ,
,  ,
, 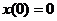 ,
,  .
. ,
,  .
.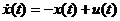 ,
,  ,
, 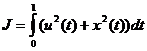 .
. ,
, 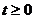 .
. 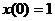 ,
,  ,
,  ,
, 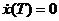 ,
,  .
.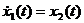 ,
, 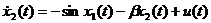 ,
,  ,
,  ,
,  .
. ,
, 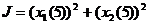 .
. ,
,  ,
,  ,
,  .
. ,
, 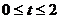 ,
,  ,.
,. ,
,  .
. ,
,  ,
,  ,
,  ,
, .
. ,
,  ,
, 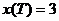 ,
, 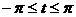 ,
,  ,
,  .
. ,
,  .
. ,
,  .
. ,
,  .
. ,
,  ,
,  ,
,  ,
, 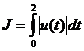 .
. ,
, 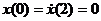 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
,  .
. ,
, 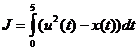 .
. ,
,  .
. ,
,  .
. ,
,  ,
,  ,
,  ,
, 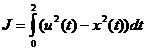

 ,
,