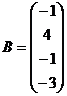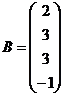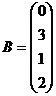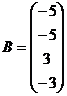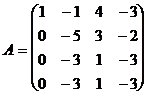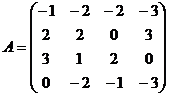Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дослідження керовності механічних коливних системЛітература:[3, с. 82-95] Мета роботи: Вивчити теоретичні критерії дослідження керовності лінійних систем керування і навчитись застосовувати їх для аналізу механічних коливних систем.
Зміст роботи:Побудувати математичну модель механічної коливної системи як системи керування і дослідити її керовність, використовуючи пакети Maple, Mathcad чи Matlab.
Методичні вказівки
Використаємо такі позначення:
Запишемо для матеріальної точки другий закон Ньютона:
Якщо запровадити додаткові змінні система (2.1) набуде вигляду
або у матричній формі
де
Як відомо [3], для того щоб система (2.2) зі сталими матрицями
де
Дослідимо керовність системи, наведеної у прикладі (2.1). Для неї і 
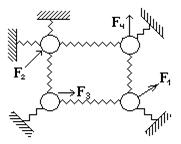
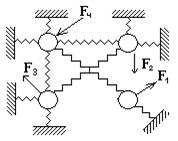
Завдання для самостійної роботи Задається механічна коливна система та набір прикладених до неї сил Для формування матриці
1.
3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27.
Лабораторна робота №3 Модальні регулятори та їх реалізація Література:[3, c.123-131], [4].
Мета роботи: Застосувати теорію з проблем модального керування об’єктами до розробки алгоритму побудови модального регулятора для заданої лінійної системи керування. Скласти і налагодити програму комп’ютерної реалізації алгоритму
Зміст роботи:Реалізувати обчислення матриці оберненого зв’язку для побудови модального регулятора, наприклад, за допомогою одного з пакетів Maple, Mathcad чи Matlab.
Методичні вказівки Розглянемо лінійну стаціонарну систему керування
де
Коефіцієнти
. . . . . . . . . . . . .
де Часто спектр матриці
Тоді однозначно відновлюються коефіцієнти характеристичного рівняння
наприклад за рекурентними співвідношеннями
Відповідь про існування шуканої матриці Теорема. Якщо система (1) є цілком керовною, тобто якщо
Розглянемо два випадки: 1.
2.
де
Обидві підсистеми
Завдання для самостійної роботи Для заданих матриць
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28.
Лабораторна робота №4 |
||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 263. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 матеріальної точки, прикріп-леної до горизонтальної і верти-кальної пружин.
Запровадимо прямокутну сис-тему координат, початок якої розта-шуємо в положенні рівноваги матеріальної точки, а осі напрямимо вздовж пружин (див. Рис. 1).
матеріальної точки, прикріп-леної до горизонтальної і верти-кальної пружин.
Запровадимо прямокутну сис-тему координат, початок якої розта-шуємо в положенні рівноваги матеріальної точки, а осі напрямимо вздовж пружин (див. Рис. 1).
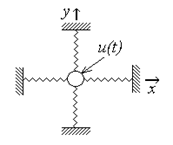 Рис. 1
Рис. 1
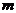 - маса матеріальної точки;
- маса матеріальної точки; - жорсткість пружини, розташованої вздовж осі ОХ;
- жорсткість пружини, розташованої вздовж осі ОХ; - жорсткість пружини, розташованої вздовж осі ОУ;
- жорсткість пружини, розташованої вздовж осі ОУ; - кут між напрямком дії сили
- кут між напрямком дії сили 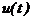 та віссю ОХ;
та віссю ОХ; 
 - координати відхилення матеріальної точки від положення рівноваги в момент часу
- координати відхилення матеріальної точки від положення рівноваги в момент часу  .
.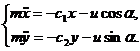 (2.1)
(2.1) то
то ,
,  (2.2)
(2.2) ,
,  ,
,  ,
,  .
. і
і  була цілком керовною, необхідно і досить, щоб виконувалась умова:
була цілком керовною, необхідно і досить, щоб виконувалась умова:
 (2.3)
(2.3) -розмір вектора
-розмір вектора 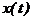 . Для одновимірного вектора керування
. Для одновимірного вектора керування  умова (2.3) еквівалентна
умова (2.3) еквівалентна . (2.4)
. (2.4)
 , отже система (2.1) буде цілком керовною, якщо
, отже система (2.1) буде цілком керовною, якщо  ,
,  та
та  .
. . Визначити, при якій найменшій сукупності сил
. Визначити, при якій найменшій сукупності сил 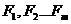
 система керування є цілком керовною.
система керування є цілком керовною. із умови (2.3) і знаходження її рангу можна скористатись стандартними пакетами Maple, Matcad чи Matlab.
із умови (2.3) і знаходження її рангу можна скористатись стандартними пакетами Maple, Matcad чи Matlab.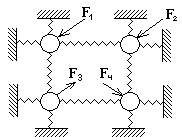 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 
 , (3.1)
, (3.1) – вектор розміру
– вектор розміру  – вектор розміру
– вектор розміру  . Важливою характеристикою для дослідження стійкості тривіального розв’язку, а також частот резонансу системи (1) є спектр матриці
. Важливою характеристикою для дослідження стійкості тривіального розв’язку, а також частот резонансу системи (1) є спектр матриці  .
. характеристичного многочлена можна обчислити методом Левер’є за такою схемою:
характеристичного многочлена можна обчислити методом Левер’є за такою схемою: ,
,  ,
,  ,
, ,
, 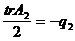 ,
,  ,
, ,
,  ,
,  ,
, ,
,  ,
,  ,
, – слід матриці
– слід матриці  ,
, 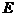 - одинична матриця порядку
- одинична матриця порядку  , де
, де  – матриця розміру
– матриця розміру  , щоб матриця
, щоб матриця 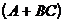 одержаної замкненої системи мала який завгодно, наперед заданий спектр
одержаної замкненої системи мала який завгодно, наперед заданий спектр  .
.
 ,
, ;
;  ,
,  ,
, 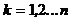 .
.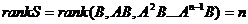 , то матрицю
, то матрицю  (сигнал управління
(сигнал управління  є одновимірним). Тоді
є одновимірним). Тоді 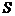 є матрицею розміру
є матрицею розміру  ,
,  ,
,  , де
, де  – матриця розміру
– матриця розміру 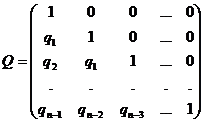 ,
, – вектор коефіцієнтів характеристичного многочлена матриці
– вектор коефіцієнтів характеристичного многочлена матриці 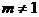 (сигнал управління
(сигнал управління 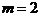 :
:  ,
,  – вектор-стовпці розміру
– вектор-стовпці розміру  виконується:
виконується:  , то побудова модального регулятора легко зводиться до відповідної задачі з одновимірним сигналом керування. Інакше, позначимо ранг матриці
, то побудова модального регулятора легко зводиться до відповідної задачі з одновимірним сигналом керування. Інакше, позначимо ранг матриці 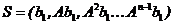 через
через  (
(  ). Тоді вектор-стовпці матриці
). Тоді вектор-стовпці матриці  є лінійно незалежними. Зробимо у системі (1) заміну змінних
є лінійно незалежними. Зробимо у системі (1) заміну змінних  ,
,  , де стовпці
, де стовпці  вибираються так, щоб
вибираються так, щоб  . Тоді система (3.1) набуде вигляду
. Тоді система (3.1) набуде вигляду , (3.2)
, (3.2) ,
,  ,
,  ,
,  ,
,  ,
, ,
,  ,
,  ,
,  .
. і
і  є цілком керовними. Тобто задача побудови модального регулятора зводиться до двох підзадач меншого розміру з одновимірними сигналами керування.
є цілком керовними. Тобто задача побудови модального регулятора зводиться до двох підзадач меншого розміру з одновимірними сигналами керування. підібрати такий обернений зв’язок
підібрати такий обернений зв’язок 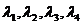 , значення яких вводяться в інтерактивному режимі. Проведення відповідних розрахунків можна виконувати засобами стандартних пакетів Maple, Mathcad чи Matlab.
, значення яких вводяться в інтерактивному режимі. Проведення відповідних розрахунків можна виконувати засобами стандартних пакетів Maple, Mathcad чи Matlab.