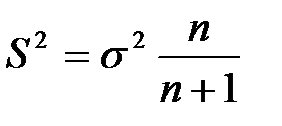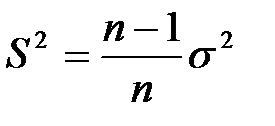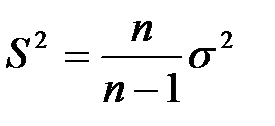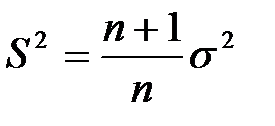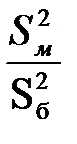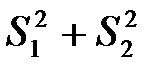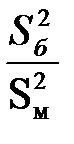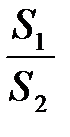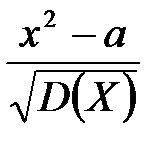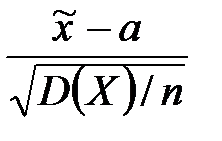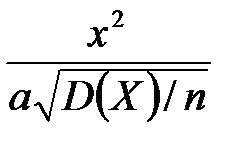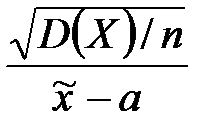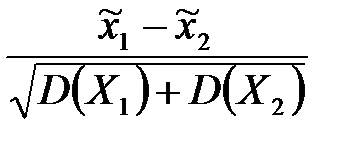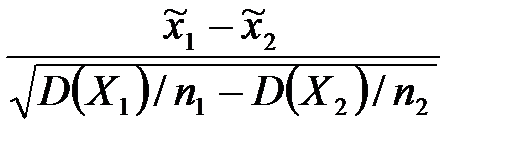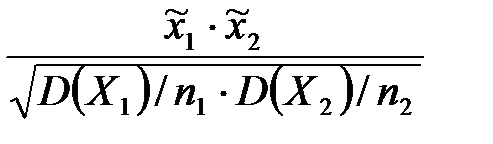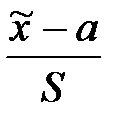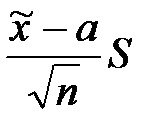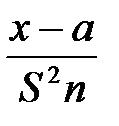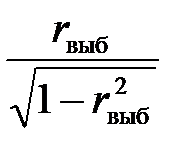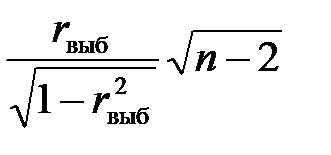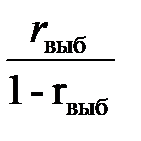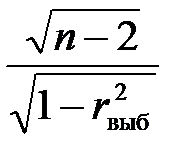Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Статистическая проверка гипотез. ⇐ ПредыдущаяСтр 5 из 5
При статистической проверке гипотез уровнем значимости вероятность допустить ошибку 1 – ого рода, т.е. принять правильную нулевую гипотезу +вероятность допустить ошибку 1 – ого рода, т.е. отвергнуть правильную нулевую гипотезу вероятность допустить ошибку 2 – ого рода, т.е. отвергнуть правильную нулевую гипотезу вероятность допустить ошибку 2 – ого рода, т.е. принять неправильную нулевую гипотезу
Критической областью называется множество значений критерия, где + множество значений критерия, при которых область, в которой область, в которой
Тип (вид) критической области определяется уровнем значимости знаком в нулевой гипотезе знаком +знаком неравенства в альтернативной гипотезе
По данным выборки > или +< или только только <
Статистические гипотезы выдвигаются о выборочных совокупностях, а проверяются по генеральным совокупностям выдвигаются о выборочных совокупностях, а проверяются тоже по выборочным совокупностям +выдвигаются о генеральных совокупностях, а проверяются по выборочным совокупностям выдвигаются о генеральных совокупностях, а проверяются тоже по генеральным совокупностям
Проверяемая гипотеза обозначается +
Множество всех значений критерия, при которых областью определения областью принятия гипотезы +критической областью областью существования 
Форма критической области (левая, правая, двусторонняя) зависит от гипотезы +гипотезы сочетания гипотезы
При статистической проверке гипотез критические точки это множество точек, образующих область принятия множество точек, образующих область принятия +точки, разделяющие область принятия гипотезы область существования
Гипотеза лежит в критической области +лежит в области принятия гипотезы лежит в области существования лежит на границе критической области и области принятия гипотезы
Гипотеза + лежит в критической области лежит в области принятия гипотезы лежит в области существования лежит на границе критической области
При статистической проверке гипотез наблюдаемое значение критерия определяется из таблиц +вычисляется по исходным данным дается в условиях задачи не используется
При статистической проверке гипотез критическое значение критерия + определяется из таблиц вычисляется по исходным данным дается в условиях задачи не используется
При статистической проверке гипотез критерием называется константа, которая находится из условий задачи любая случайная величина +случайная величина с известным распределением константа, которая находится из таблиц
По данным выборки +> или < или только только <
По данным выборки < или +> или только только <
По данным выборки >или только только > +< или
При проверке гипотезы о равенстве генеральных дисперсий в качестве критерия используется случайная величина, имеющая распределение +Фишера – Снедекора (F) Стьюдента (T) нормальное (Z) Пирсона
При проверке гипотезы о равенстве генеральных средних (малые выборки Фишера – Снедекора (F) +Стьюдента (T) нормальное (Z) Пирсона
При проверке гипотезы о равенстве генеральных средних(большие выборки Фишера – Снедекора (F) Стьюдента (T) +нормальное (Z) Пирсона
Альтернативная (конкурирующая) обозначается +
Стандартный размер > или ¹ +< или ¹ только ¹ только<
Уровень значимости определяет тип критической области +значение формулировку нулевой гипотезы формулировку конкурирующей гипотезы
Конкурирующая гипотеза определяет +тип критической области размер критической области распределение случайной величины, используемой в качестве критерия при проверке гипотезы область принятия гипотезы
Если принимается гипотеза +первый станок налажен лучше второй станок налажен лучше станки налажены одинаково нельзя сделать вывода
К непараметрическим относятся гипотезы о равенстве генеральных средних о равестве генеральных дисперсий +о законах распределения об уровне значимости
Если конкурирующая гипотеза имеет вид +правосторонняя левосторонняя двусторонняя любая
Если конкурирующая гипотеза имеет вид правосторонняя двусторонняя +левосторонняя любая
Если конкурирующая гипотеза имеет вид любая +двусторонняя правосторонняя левосторонняя
Если конкурирующая гипотеза имеет вид + двусторонняя левосторонняя любая правосторонняя
Двусторонняя критическая область соответствует гипотезе +
Если принимается гипотеза первый станок налажен лучше второй налажен лучше станки налажены неодинаково +станки налажены одинаковы
Если принимается гипотеза +вес детали соответствует стандарту тяжелее стандарта легче стандарта нельзя сделать вывода
Малые выборки +
Большие выборки +
При статистической проверке гипотезы о равенстве генеральных дисперсий в качестве критерия используется случайная величина, имеющая распределение Стьюдента (Т) +Фишера – Снедекора (F) нормальное (Z) Пирсона
При статистической проверке гипотезы о равенстве генеральных средних, в случае, когда генеральные дисперсии известны, используется случайная величина, имеющая распределение Фишера – Снедекора (F) + нормальное(Z) Стьюдента(Т) Пирсона
При статистической проверке гипотезы о равенстве генеральной средней стандарту (генеральная дисперсия неизвестна) в качестве критерия используется случайная величина, имеющая распределение +Стьюдента (Т) нормальное (Z) Фишера – Снедекора (F) Пирсона
При статистической проверке гипотезы о равенстве генеральной средней стандарту (генеральная дисперсия известна) в качестве критерия используется случайная величина, имеющая распределение + нормальное (Z) Фишера – Снедекора (F) Пирсона Стьюдента (Т)
При статистической проверке гипотезы о равенстве генеральных средних (генеральные дисперсии неизвестны, но равны) в качестве критерия используется случайная величина, имеющая распределение Пирсона нормальное (Z) + Стьюдента (Т) Фишера – Снедекора (F)
Правильная форма нулевой гипотезы +
Альтернативная гипотеза имеет вид правосторонняя произвольная +левосторонняя двусторонняя
Границей между критической областью и областью принятия нулевой гипотезы является прямая окружность +точка парабола
По данным выборки +> или ≠
< или ≠ только ≠ только <
Альтернативная гипотеза имеет вид правосторонняя +двусторонняя произвольная левосторонняя
Исправленная выборочная дисперсия определяется по формуле + Наблюдаемое значение критерия Фишера – Снедекора равно + Наблюдаемое значение критерия Z (проверка гипотезы о равенстве генеральной средней стандарту; D(X) известна) определяется формулой + Наблюдаемое значение критерия Z (при проверке гипотезы о равенстве генеральных средних; D(X) известна) определяется формулой + Наблюдаемое значение критерия Стьюдента (проверка гипотезы о равенстве генеральной средней стандарту; генеральная дисперсия неизвестна) определяется формулой + Наблюдаемое значение критерия Стьюдента при проверке гипотезы о значимости выборочного коэффициента корреляции определяется по формуле +
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 280. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
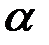 называется
называется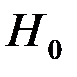 принимается
принимается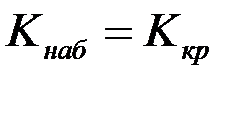
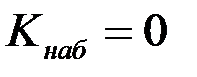
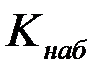
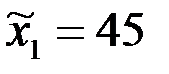 ;
; 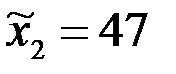 . При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак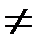
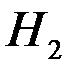
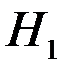
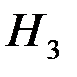
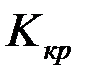
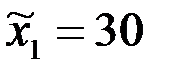 ;
; 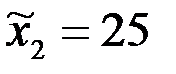 . При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак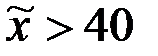 . При проверке гипотезы о равенстве генеральной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак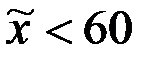 . При проверке гипотезы о равенстве генеральной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак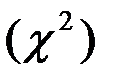
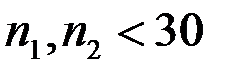 ) используется случайная величина, имеющая распределение
) используется случайная величина, имеющая распределение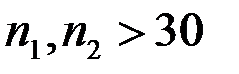 ) используется случайная величина, имеющая распределение
) используется случайная величина, имеющая распределение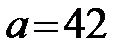 . По данным выборки размер
. По данным выборки размер 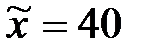 . При проверке гипотезы о равенстве генеральной средней стандарту в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральной средней стандарту в конкурирующей гипотезе должен быть знак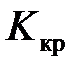
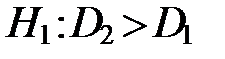 о работе двух станков, то
о работе двух станков, то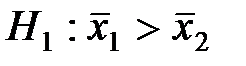 , то критическая область
, то критическая область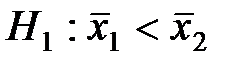 , то критическая область
, то критическая область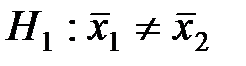 , то критическая область
, то критическая область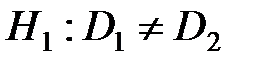 , то критическая область
, то критическая область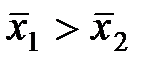
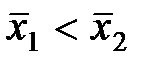
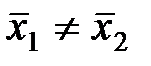
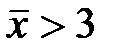
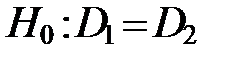 о работе двух станков, то
о работе двух станков, то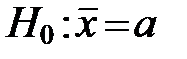 о весе детали, то
о весе детали, то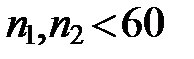
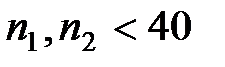
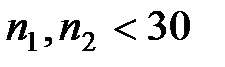
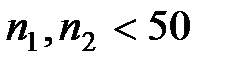

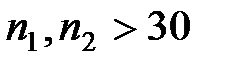
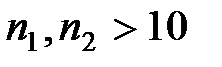
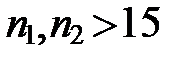
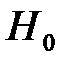 имеет вид
имеет вид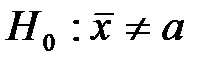
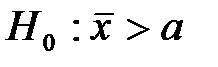
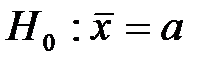
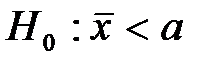
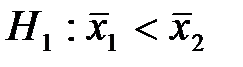 . Критическая область -
. Критическая область - ,
, 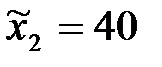 . При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральных средних в конкурирующей гипотезе должен быть знак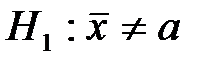 . Критическая область -
. Критическая область -