Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Повторные независимые испытания
Повторными независимыми испытаниями относительно события А называются испытания которые повторяются которые повторяются и не зависят от других испытаний +которые проводятся в одних и тех же условиях и с одинаковой вероятностью появления события А в каждом испытании в которых событие А повторяется
Вероятность появления события А m раз в n повторных независимых испытаниях при +формулой Бернулли локальной теоремой Лапласа интегральной теоремой Лапласа формулой Пуассона
Наивероятнейшим числом наступлений события А в n независимых испытаниях называется наибольшее число наступлений события А наибольшая вероятность наступления события А число наступлений события А при наибольшем числе испытаний + число наступлений события А, при котором вероятность наступления события А в n независимых испытаниях наибольшая
Функция четная возрастающая нечетная убывающая +четная положительная нечетная положительная
Функция + нечетная возрастающая четная возрастающая нечетная убывающая четная убывающая
Локальная теорема Лапласа позволяет вычислить наивероятнейшее число наступлений события в n независимых испытаниях относительную частоту наступлений события в n независимых испытаниях +вероятность появления события m раз в n независимых испытаниях (n >10) вероятность отклонения числа появлений события m от числа независимых испытаний n
Интегральная теорема Лапласа позволяет вычислить вероятность появления события A m раз в n испытаниях (n >10)  + вероятность появления события A в n испытаниях не менее а, но не более наивероятнейшее число появлений события A в n независимых испытаниях (n >10) относительную частоту наступлений события A в n независимых испытаниях
Из следствия из интегральной теоремы Лапласа следует что относительная частота поступлений события равна вероятности появления этого события относительная частота наступлений события отклонится от вероятности появления этого события с увеличением числа n независимых испытаний вероятность наступления события увеличивается +с увеличением числа испытаний n относительная частота
Математическое ожидание случайной величины – числа появлений события А в n независимых испытаниях с вероятностью p наступления события А – равно +
Дисперсия случайной величины – числа появлений события А в n независимых испытаниях с вероятностью p наступления события А – равна + p
Вероятность появления события А m раз в n независимых испытаниях зависит только от m и n +зависит от m, n и p зависит только от m не зависит от m и n
Вероятность появления события А m раз в n повторных независимых испытаниях при +
Вероятность +
В локальной теореме Лапласа +
В интегральной формуле Лапласа +
В интегральной формуле Лапласа +
вероятность наивероятнейшей частоты +вероятность того, что при условная вероятность события вероятность, что при повторных испытаниях событие произойдет от
При повторных независимых испытаниях используются формулы: а) Бернулли; б) Локальная Лапласа; в) Интегральная Лапласа. Точными являются б) +a) в) б), в)
+от а (включительно) до b в (включительно раз больше а и меньше b раз
Наивероятнейшее число только одно значение +либо одно, либо два значения обязательно два значения три значения
Для случайной величины – числа появлений события А в n независимых испытаниях с вероятностью p наступления события А выражение np является дисперсией вариацией средним квадратическим отклонением +математическим ожиданием
Для случайной величины – числа появлений события А в n независимых испытаниях с вероятностью p наступления события А выражение математическим ожиданием +дисперсией вариацией средним квадратическим отклонением
Математическое ожидание случайной величины – числа наступлений события А с вероятностью 45 50 30 +40
Дисперсия случайной величины – числа наступлений события А с вероятностью 30 +21 39 23
Вероятность появления события +
Формула для определения наивероятнейшего числа +
Вероятность появления события А m раз в n повторных независимых испытаниях при +
Выражение +локальной теореме Лапласа интегральной теореме Лапласа формуле Бернулли формуле Пуассона
С вероятностью, близкой к +
В следствии интегральной теоремы Лапласа +
При достаточно большом числе испытаний абсолютная величина величина отклонения частости (относительной частоты, доли) +
Если проводится n независимых испытаний, то в каждом из них событие А может произойти с вероятностью p или не произойти с вероятностью +
Вероятность наступления события формулой Пуассона формулой Бернулли +локальной теоремой Лапласа интегральной теоремой Лапласа
Формула локальную теорему Лапласа интегральную теорему Лапласа формулу Пуассона +следствие интегральной теоремы Лапласа
Выражение + следствии интегральной теоремы Лапласа локальной теореме Лапласа интегральной теореме Лапласа формуле Пуассона
Если число независимых испытаний n=100, а математическое ожидание случайной величины равно 40, то вероятность наступления события А в каждом из этих испытаний равна 0,2 +0,4 0,6 0,8
Если вероятность наступления события А в каждом из n независимых испытаний равна 0,6, а математическое ожидание равно 120, то n равно 100 +200 500 1000
Указать число повторных независимых испытаний, при котором не рекомендуется использовать формулу Бернулли 6 8 10 +12
Указать число повторных независимых испытаний, при котором рекомендуется использовать локальную теорему Лапласа 5 8 10 +13
Вероятность наступления события А в каждом из n повторных независимых испытаний равна p=0,7, а дисперсия равна 21. Число n равно 50 +100 10 150
Число наступлений события А, при котором вероятность наступления события А в n независимых испытаниях наибольшая, называется наибольшей вероятностью +наивероятнейшим числом наибольшим числом наивероятнейшим событием
В выражении +
Величина математическое ожидание +среднее квадратичное отклонение дисперсию вариацию
Если число независимых испытаний 1 3 +5 7
Предел функции -1 0 1/2 +1 Для функции +
Для значений +
Для функции +
Функция -1 +0 1
При увеличении числа испытаний в бесконечном числе испытаний в +в одном испытании в десяти испытаниях
В выражении дисперсией средне – квадратическим отклонением +математическим ожиданием вероятностью наступления события в одном испытании Предел функции -1 +0 1
Закон больших чисел Закон больших чисел – это действия над большими числами правила выполнения арифметических действий над большими числами закон распределения большого числа случайных величин +группа теорем о средних характеристиках случайных величин при большом числе испытаний
Последовательность случайных величин +
Лемма Маркова оценивает вероятность того, что положительная случайная величина Х не превзойдет ее дисперсии ее среднего квадратического отклонения предельной ошибки +
Из обобщенной теоремы Чебышева следует, что если дисперсии попарно независимых случайных величин ограничены сверху константой средняя арифметическая случайных величин равна средней арифметической их математических ожиданий средняя арифметическая случайных величин равна математическому ожиданию одной из них средняя арифметическая случайных величин больше средней арифметической их математических ожиданий + средняя арифметическая случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий
Из обобщенной теоремы Чебышева следует, что равна 1 равна 0 +больше, чем равна
Неравенство Чебышева оценивает вероятность того, что отклонение случайной величины Х от ее математического ожидания положительно отрицательно +по абсолютной величине не превзойдет определенного положительного числа по абсолютной величине превзойдет определенное положительное число
Из неравенства Чебышева с вероятностью, большей, чем больше, чем +не превзойдет равна равна 0
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 314. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
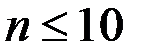 определяется
определяется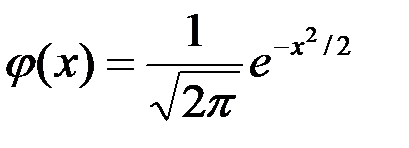 обладает следующими свойствами
обладает следующими свойствами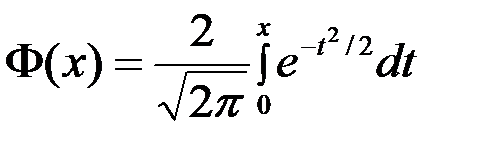 обладает следующими свойствами
обладает следующими свойствами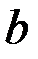 раз (n >10)
раз (n >10)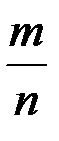 приближается к вероятности появления события в одном испытании
приближается к вероятности появления события в одном испытании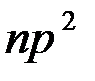
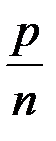
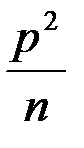
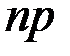
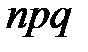
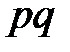
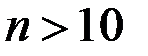 определяется формулой
определяется формулой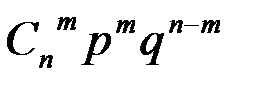
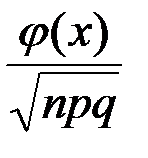
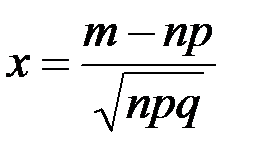
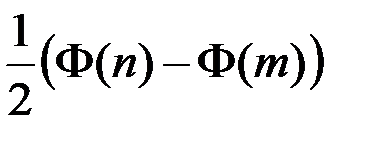
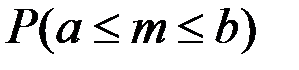 появления события А в n повторных независимых испытаниях (n >10) равна
появления события А в n повторных независимых испытаниях (n >10) равна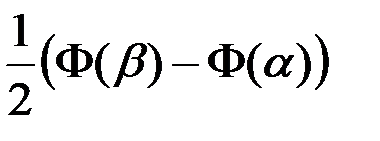
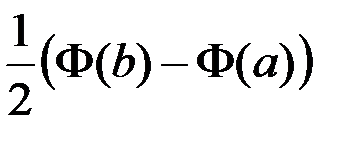
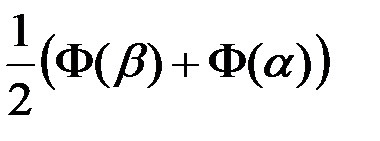
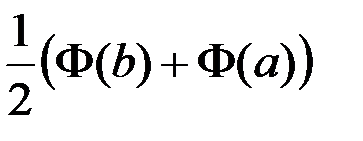
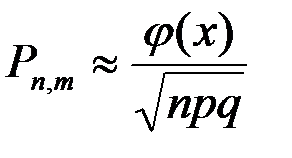 аргумент функции
аргумент функции 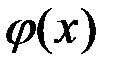 равен
равен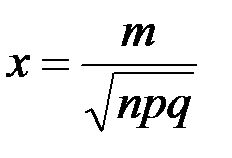
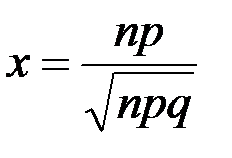
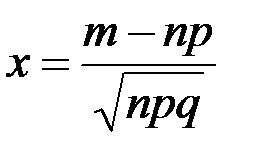
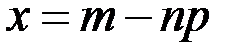
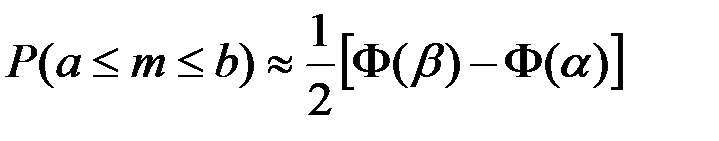 , аргумент
, аргумент 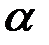 функции
функции 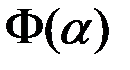 равен
равен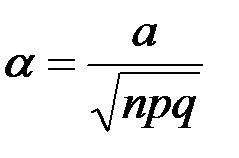
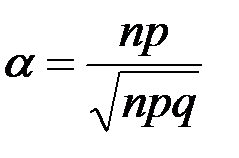
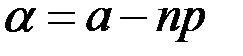
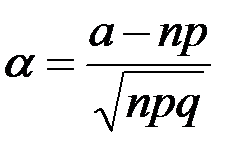
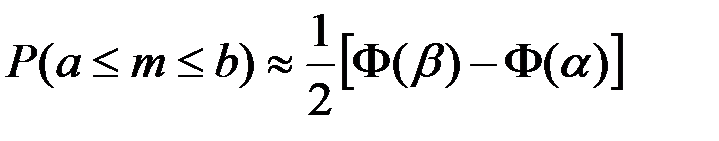 , аргумент
, аргумент 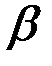 функции
функции 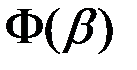 равен
равен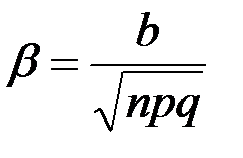
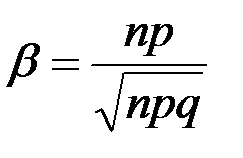
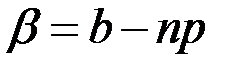
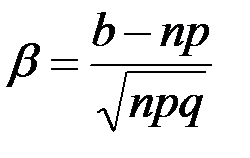
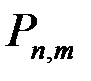 это
это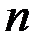 испытаниях события наступит равно
испытаниях события наступит равно 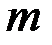 раз
раз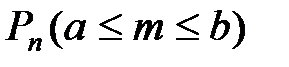 это вероятность того, что при
это вероятность того, что при 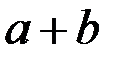 раз
раз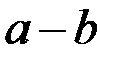 раз
раз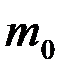 может иметь
может иметь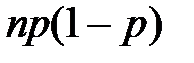 является
является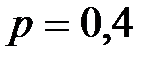 в
в 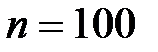 независимых испытаниях равно
независимых испытаниях равно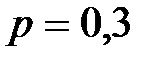 в
в 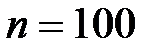 независимых испытаниях равна
независимых испытаниях равна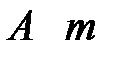 раз в
раз в 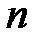 повторных независимых испытаниях определяется формулой Бернулли при
повторных независимых испытаниях определяется формулой Бернулли при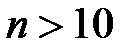
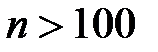
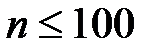
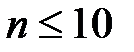
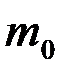 имеет вид
имеет вид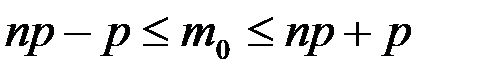
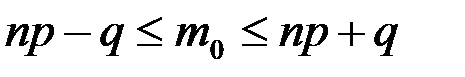
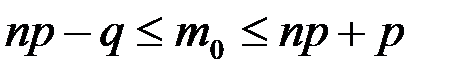
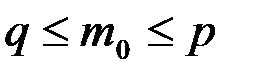
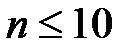 определяется формулой
определяется формулой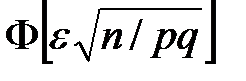 , можно утверждать, что при достаточно большом числе испытаний абсолютная величина отклонения частости (относительной частоты, доли)
, можно утверждать, что при достаточно большом числе испытаний абсолютная величина отклонения частости (относительной частоты, доли) 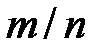 события А от его вероятности p не превзойдет положительного числа
события А от его вероятности p не превзойдет положительного числа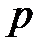
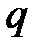
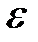
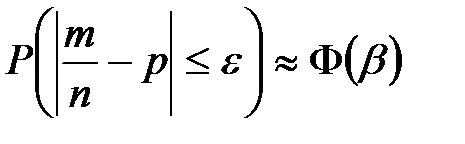 аргумент функции
аргумент функции 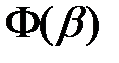 равен
равен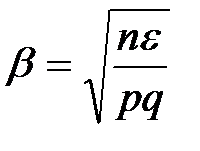
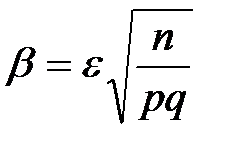
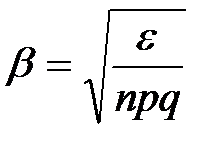
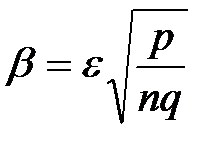
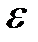 с вероятностью, близкой к
с вероятностью, близкой к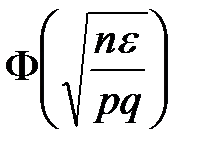
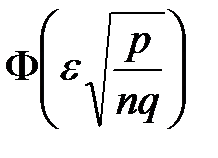
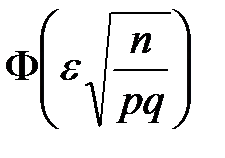
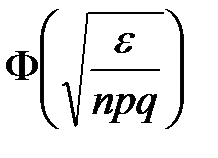
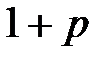
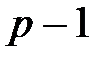
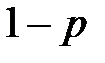
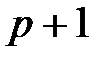
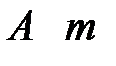 раз в n повторных независимых испытаниях при
раз в n повторных независимых испытаниях при 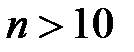 определяется
определяется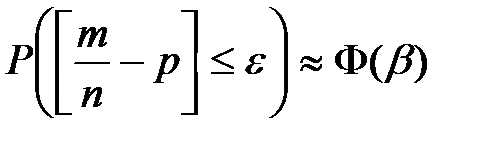 , где
, где 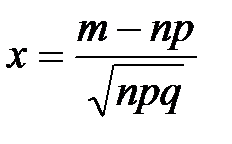 средним квадратичным отклонением является величина
средним квадратичным отклонением является величина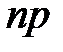
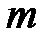
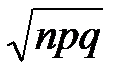
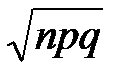 в выражении
в выражении 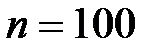 , а математическое ожидание случайной величины равно 50, то среднее квадратичное отклонение равно
, а математическое ожидание случайной величины равно 50, то среднее квадратичное отклонение равно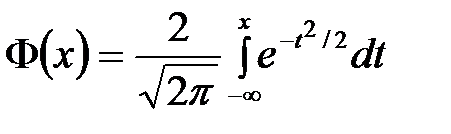 при
при 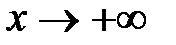 равен
равен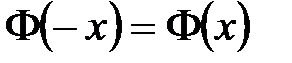
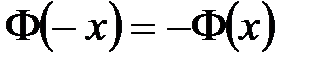
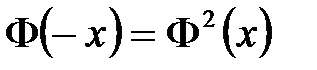
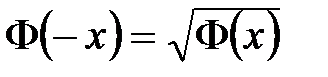
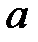 и
и 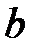 из интегральной теоремы Лапласа имеют место соотношения
из интегральной теоремы Лапласа имеют место соотношения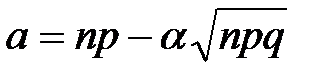 ,
, 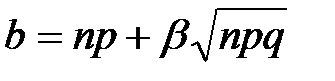
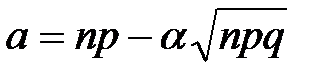 ,
, 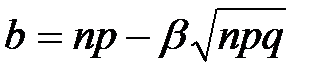
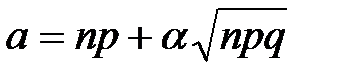 ,
, 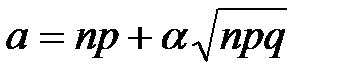 ,
, 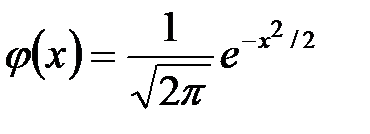 выполняется
выполняется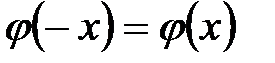
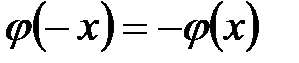
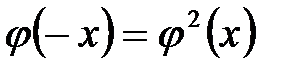
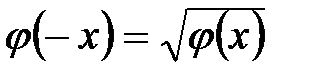
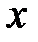 , равном
, равном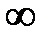
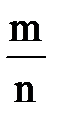 приближается к вероятности появления события
приближается к вероятности появления события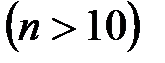
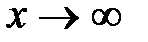 равен
равен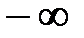
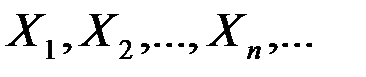 называется сходящейся по вероятности при
называется сходящейся по вероятности при 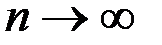 к случайной величине Х, если при любом сколь угодно малом
к случайной величине Х, если при любом сколь угодно малом 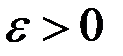
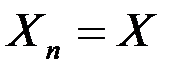
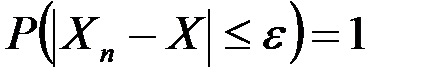
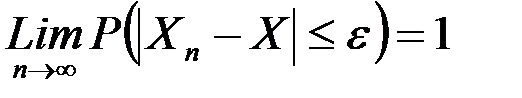
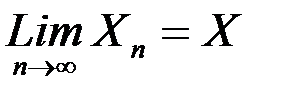
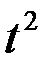 - кратного математического ожидания
- кратного математического ожидания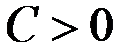 , то
, то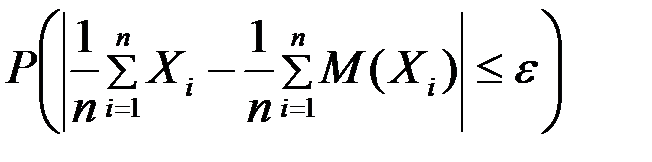
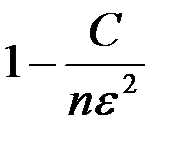
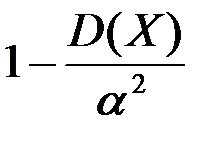 можно утверждать, что абсолютная величина отклонения случайной величины Х от ее математического ожидания
можно утверждать, что абсолютная величина отклонения случайной величины Х от ее математического ожидания