
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Случайная величина. Числовые характеристики случайной величины. Случайные процессы.Стр 1 из 5Следующая ⇒
Математическое ожидание случайной величины (с X+Y),где +
Дисперсия случайной величины (с X+Y),где +
Дисперсия разности двухнезависимых случайных величин X иY равна 0 +
Математическое ожидание произведения двух независимых случайных величин X и Y равно +
Индикатором события А называется случайная величина, которая равна константе а>1 равна константе а<-1 всегда равна 1 +равна 1, если в результате испытания событие А происходит и равна 0, если событие А не происходит
Законом распределения дискретной случайной величины называется соответствие между возможными значениями случайной величины и рядом натуральных чисел + возможными значениями случайной величины и вероятностями их появления математическим ожиданием случайной величины и ее средним квадратическим отклонением возможными значениями случайной величины и ее математическим ожиданием
Сумма всех вероятностей значений дискретной случайной величины равна 0 +1 -1
Математическое ожидание дискретной случайной величины вычисляется по формуле + Математическое ожидание постоянной величины С равно +С 1 0 не определено
Математическое ожидание случайной величины (с X-Y),где +
Дисперсия дискретной случайной величины определяется по формуле +
Существуют две формы задания закона распределения дискретной случайной величины: интегральная и дифференциальная  интегральная и табличная +табличная и графическая графическая и интегральная
Дисперсия постоянной величины С равна 1 C +0 не определена
Среднее квадратическое отклонение + M(X)
Дисперсия от математического ожидания М(Х) +0 Х 1
Математическое ожидание от математического ожидания +M(X) 0 1 D(X)
Математическое ожидание M(X) D(X) +0 1
Математическое ожидание квадрата отклонения +D(X) M(X) V
Математическое ожидание M(X) случайной величины Х есть переменная величина +¥ -¥ +постоянная величина
Дисперсия +
Существует две формы задания непрерывной случайной величины +функция распределения и плотность распределения вероятностей ряд распределения и полигон функция распределения и ряд распределения функция распределения и полигон
Выражение дисперсией дискретной случайной величины вариацией дискретной случайной величины +математическим ожиданием дискретной случайной величины средним квадратическим отклонением
Выражение +дисперсией дискретной случайной величины вариацией дискретной случайной величины математическим ожиданием дискретной случайной величины средним квадратическим отклонением
Величина, которая в зависимости от результатов испытаний принимает то или иное численное значение, называется постоянной величиной переменной величиной +случайной величиной нормальной величиной
Случайные величины делятся на переменные и постоянные четные и нечетные рациональные и нерациональные +дискретные и непрерывные
Дискретной называется такая случайная величина, которая принимает +конечное или бесконечное счетное множество значений бесконечное множество значений только одно значение только отрицательные значения
Графическая форма задания закона распределения случайной величины – это парабола прямая линия окружность +полигон
Табличная форма задания закона распределения случайной величины называется суммой распределения интегралом распределения +рядом распределения полем распределения
Непрерывная случайная величина имеет конечное множество значений бесконечное счетное множество значений конечное или бесконечное счетное множество значений +бесконечное несчетное множество значений
Дисперсией случайного процесса математическому ожиданию соответствующего сечения случайного процесса +дисперсии соответствующего сечения случайного процесса среднему квадратическому отклонению соответствующего сечения случайного процесса вариации соответствующего сечения случайного процесса
Случайный процесс +
2Корреляционной функцией случайного процесса сумме математических ожиданий соответствующих сечений случайного процесса сумме дисперсий соответствующих сечений случайного процесса +ковариации соответствующих сечений случайного процесса произведению дисперсий соответствующих сечений случайного процесса
Случайный процесс с дискретным временем (t принимает целочисленные значения) называется целочисленным рядом целочисленной последовательностью целочисленным случайным процессом + временным рядом
Процесс изменения во времени состояния какой – либо системы в соответствии с вероятностными закономерностями называется закономерным процессом переменным процессом +случайным процессом составным процессом
Неслучайная функция дисперсией случайного процесса +математическим ожиданием случайного процесса огибающей случайного процесса направляющей случайного процесса
Если +1 3 5 7
Если 1 +5 13 16
Если 1 3 +5 9 Если 1 3 +5 17
Указать неверное значение дисперсии +-1 4 9 16
Указать верное значение дисперсии -9 -4 +1 -1
Дискретная случайная величина принимает только множество целых значений только множество положительных значений все значения из интервала +конечное или бесконечное счетное множество значений.
Непрерывная случайная величина принимает множество целых значений множество рациональных значений конечное множество значений +любое значение из конечного или бесконечного интервала
Для непрерывной случайной величины +0 1/2 1
Если + Если -2 -1 +0,5 Если +-1 0,1 0,4 1 Математическое ожидание + Если -1 0 +1 Если + Если + Если + Если 1 0,4 0,6 +1,2 Случайная величина, принимающая конечное или бесконечное счетное множество значений, называется +дискретной конечной бесконечной непрерывной
Случайная величина, принимающая любые значения из конечного или бесконечного интервала, называется дискретной конечной бесконечной + непрерывной
Если 1 3 +5 7
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 310. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  - независимые случайные величины, равно
- независимые случайные величины, равно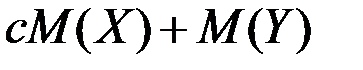


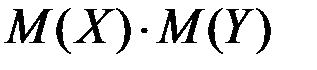






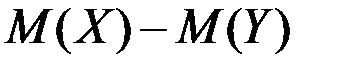


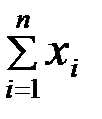





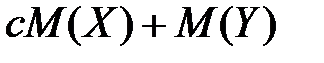




 случайной величины Х равно
случайной величины Х равно


 равна
равна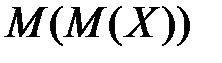 равно
равно равно
равно равно
равно
 , определяется формулой
, определяется формулой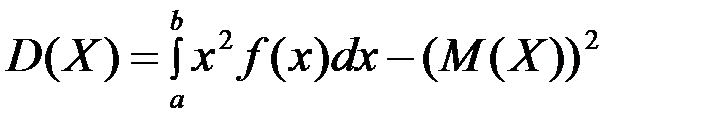



 является
является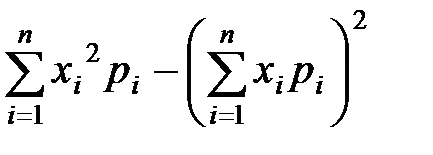 является
является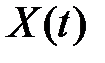 называется неслучайная функция
называется неслучайная функция  , которая при любом значении t равна
, которая при любом значении t равна и
и  ,
,  , условное распределение
, условное распределение  при условии, что заданы все значения
при условии, что заданы все значения  , зависит только от
, зависит только от


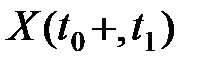
 двух аргументов
двух аргументов  и
и 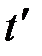 , которая при каждой паре значений
, которая при каждой паре значений  и
и 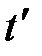 равна
равна , которая при любом значении t равна математическому ожиданию соответствующего сечения случайного процесса, называется
, которая при любом значении t равна математическому ожиданию соответствующего сечения случайного процесса, называется , а
, а  , то дисперсия случайной величины равна
, то дисперсия случайной величины равна , а
, а 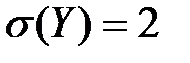 , то
, то 
 , а
, а  , то
, то 
 ; а
; а  , то
, то 

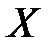 и конкретного значения
и конкретного значения 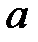 вероятность
вероятность  равна
равна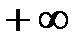
 -непрерывная случайная величина,
-непрерывная случайная величина, 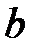 - конкретные значения, то отсюда следует, что
- конкретные значения, то отсюда следует, что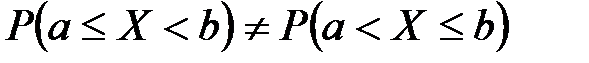


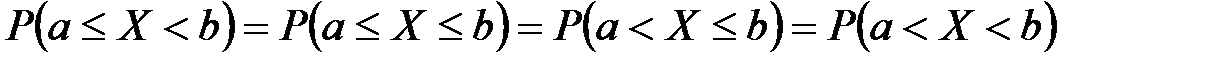
 - плотность распределения, то
- плотность распределения, то  при соответствующем значении
при соответствующем значении 
 непрерывной случайной величины
непрерывной случайной величины  , заданной на интервале
, заданной на интервале  , определяется формулой
, определяется формулой
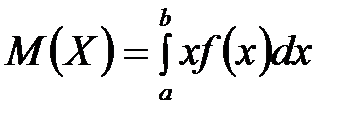


 равен
равен
 определяет
определяет

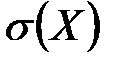

 определяет
определяет определяет
определяет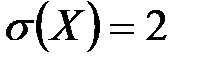 , а
, а  , то
, то  равна
равна