Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Подвижность свободных носителей заряда. Зависимость подвижности от температуры.Среди доминирующих механизмов рассеяния свободных носителей в твердых телах следует выделить рассеяние на колебаниях решетки (акустических и оптических фононах), рассеяние на заряженной примеси, рассеяние на нейтральных атомах. Для каждого из этих механизмов рассеяния характерна своя зависимость времени релаксации от энергии и температуры. Расчет зависимости времени релаксации от энергии τ(E) представляет сложную квантово-механическую задачу и выходит за рамки этого курса. Для фононного механизма рассеяния зависимость τ(E) выражается следующим соотношением:
Подставляя (10.74) в (10.71) и проводя интегрирование, получаем для усредненного времени релаксации при рассеянии на фононах
С учетом соотношения (10.75) величина подвижности свободных носителей при рассеянии на фононах будет равна
Из уравнения (10.76) следует, что подвижность свободных носителей уменьшается с ростом температуры по степенному закону. С точки зрения физики данный участок зависимости подвижности свободных носителей от температуры объясняется тем, что число фононов также возрастает с ростом температуры. Для рассеяния на атомах ионизованной примеси выражение для времени релаксации определяется соотношением
где Z – число электронов, N – концентрация примеси. Усредненное время релаксации имеет вид
Соответственно величина подвижности при рассеянии на заряженной примеси будет равна
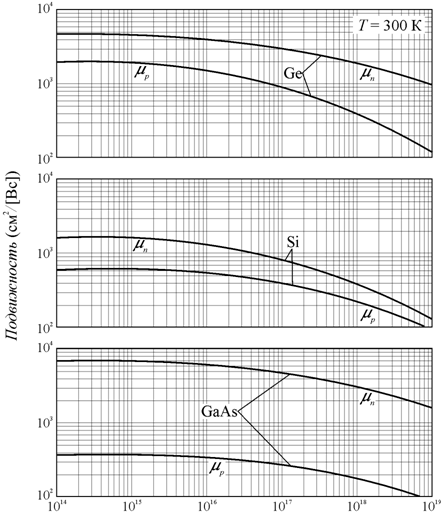
Для полупроводников роль заряженной примеси играют доноры и акцепторы. На рис. 10.13 показана экспериментальная зависимость подвижности электронов и дырок в кремнии, германии и арсениде галлия от концентрации легирующей примеси при комнатной температуре. 
При наличии в твердом теле нескольких типов центров рассеивания, вероятность рассеивания на каждом из них не зависит друг от друга, и общая вероятность рассеивания определяется суммой парциальных вероятностей:
С учетом этого должны суммироваться обратные значения времен релаксации, следовательно, для суммарного времени релаксации получаем
Аналогично получаем и для подвижности свободных носителей. В качестве примера, если в твердом теле два доминирующих механизма рассеивания (примесь и тепловые колебания решетки), то для подвижности получаем следующее соотношение:
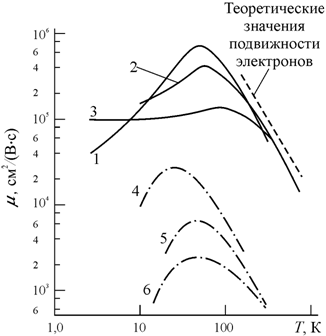
где a и b − постоянные величины. Анализ уравнения (10.82) показывает, что в разных температурных диапазонах будет доминировать тот или иной механизм рассеивания, и он будет определять величину и температурную зависимость подвижности. На рис. 10.14 показаны температурная зависимость и подвижность электронов в антимониде индия с различным уровнем концентрации легирующей примеси.
Как видно из экспериментальных данных, приведенных на рис. 10.14, и для электронов, и для дырок в области высоких температур подвижность уменьшается с ростом температуры вследствие рассеяния на акустических фононах по закону, близкому к описываемому соотношением (10.76). При низких температурах подвижность растет с ростом температуры по закону, определяемому соотношением (10.79), и этот характер обусловлен рассеянием на ионах примесей.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 476. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
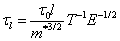 .
.
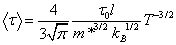 .
.
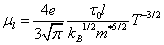 .
.
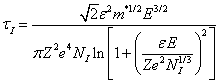 ,
,
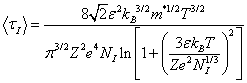 .
.
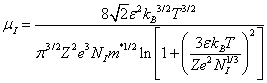 .
.
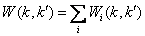 .
.
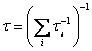 .
.
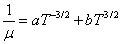 ,
,