
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Математичне сподівання, дисперсія та середнє квадратичне відхилення частоти та відносної частоти в схемі незалежних повторнитх випробувань.Стр 1 из 3Следующая ⇒ Класичне означення імовірності. Властивості імовірності. Теорема добутку імовірностей та наслідки з неї. Імовірність події A дорівнює: P(A)= m/n деn - число (кількість) подій у просторі елементарних подій, а m - число наслідків (із простору елементарних подій), які сприяють появі події A. Властивості: 1. Для довільної події A: 2.Для достовірної події U:P(U)=1 3.Для неможливої події V: P(V)=0. Теорема (добутку імовірностей). Імовірність добутку двох подій A і B дорівнює добутку імовірності однієї з них на умовну імовірність іншої, при умові, що настала перша подія:
Доведення. Нехай n - кількість подій (елементарних наслідків) у просторі елементарних подій, з яких k подій сприяють появі AB, m - сприяють появі A, а L - сприяють появі B
За класичним означенням імовірності:
Аналогічно доводиться, що P(ABC)=P(A)*Pa(B)*Pa(B). Наслідок 1 (формули визначення умовних імовірностей). Якщо імовірності подій відмінні від нуля, то
Зауважимо, що теорема добутку справедлива навіть у випадку нульових імовірностей подій Наслідок 2. Якщо подія A не залежить від події B, то і навпаки, подія B не залежить від події A, тобто вони взаємно незалежні. Доведення: Наслідок 3. Із незалежності подій A і B випливає незалежність пар подій : Наслідок 4. Імовірність добутку двох незалежних подій дорівнює добутку їх імовірностей: P(AB)=P(A)*P(B) Доведення: Теорема суми імовірностей та наслідки з неї. Теорема. Імовірність суми двох подій A і B дорівнює сумі імовірностей цих подій без імовірності їх добутку. Іншими словами, імовірність появи хоча б однієї із двох подій дорівнює сумі їх імовірностей без імовірності їх сумісної появи:  P(A+B)=P(A)+P(B)-P(AB) Доведення:
= P (A) + P (B)-P(AB) Наслідок 1. Імовірність суми двох несумісних подій дорівнює сумі їх імовірностей: P(A+B)=P(A)+P(B). Наслідок 2. Сума імовірностей подій A1, А2,.....,Аn, що утворюють повну групу, дорівнює одиниці: P (A1)+P(A2)+….+P(An)=1 Доведення:
Наслідок 3. Для взаємно протилежних подій A і
Доведення випливає із попереднього наслідка 2. Наслідок4. Імовірність появи хоча б однієї із подій A1,A2,…..,An дорівнює: Зокрема, якщо події незалежні в сукупності, то:
Доведення:
Теорема (формула повної імовірності) та формули Байєса Теорема. Нехай подія A може настати лише сумісно з хоча б однією із подій-гіпотез H1, H2….Hn , які утворюють повну групу. Тоді імовірність (повна імовірність) події A дорівнює: тобто сумі добутків імовірностей гіпотез на умовні ймовірності події, при умові, що настала відповідна гіпотеза Доведення: Формули Байєса. Теорема. Нехай подія A може настати лише сумісно з хоча б однією із подій-гіпотез H1, H2….Hn , які утворюють повну групу. Якщо подія A настала, то умовні (уточнені) імовірності гіпотез дорівнюють:
i=1,2,…….,n де повна імовірність Доведення: Зазначимо, що виконуються усі умови теореми – формули повної ймовірності. Розглянемо одну із подій AHi і скористуємось теоремою добутку: P(AHi)=P(A)Pa(Hi)=P(Hi)Phi(A). Звідси:
де P(A) - повна імовірність. Математичне сподівання, дисперсія та середнє квадратичне відхилення частоти та відносної частоти в схемі незалежних повторнитх випробувань. Знайдемо числові характеристики біноміально розподіленої ДВВ X=m. Розглянемо випадкові величини Xi=mi, i=1,2,…,n - частоту появи події A у i -тому випробуванні. Закони розподілу усіх цих ВВ однакові і мають вигляд:
Неважко переконатись, що числові характеристики цих ВВ: M(mi)=p, D(mi)=p-p^2=p(1-p)=pq. Враховуючи, що Означення. Найімовірнішою частотою За означенням із системи умов
неважко дістати подвійну нерівність для визначення найімовірнішої частоти:
ВВ X=m/n - частість (частка, відносна частота) появи події A у n НПВ також підкоряється біноміальному закону розподілу з числовими характеристиками M(m/n)=p, D(m/n)=pq/n Відзначимо, що при достатньо великій кількості випробувань n найімовірніша частота m0 приблизно дорівнює np, а найімовірніша частість приблизно дорівнює імовірності p появи події у кожному окремому випробуванні. Зауважимо також, що біноміальний розподіл при збільшенні кількості НПВ досить швидко наближається до нормального. |
||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 207. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ;
; .
. .
. .
. і
і  ,
, 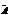 і
і  ,
,  .
.

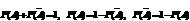 .
. .
.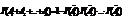 .
.
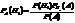 ,
,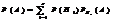
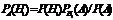 ,
,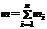 , за властивостями математичного сподівання та дисперсії дістанемо:
, за властивостями математичного сподівання та дисперсії дістанемо:  ,
,  , звідки
, звідки  .
.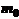 (або модою) появи події A у n НПВ називають частоту, для якої
(або модою) появи події A у n НПВ називають частоту, для якої  .
.
 .
. .
.