
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Точечные и интервальные оценки параметров распределения. Доверительная вероятность (надёжность) и доверительный интервал.
Пусть мы имеем некоторую выборку из генеральной совокупности с известным законом распределения и требуется оценить параметр  по данным выборки. Статистической оценкой неизвестного параметра по данным выборки. Статистической оценкой неизвестного параметра  генеральной совокупности называется его приближенное значение генеральной совокупности называется его приближенное значение  вычисленное по данным выборки и зависящее только от них. Чтобы оценка давала хорошее приближение, она должна быть несмещенной, эффективной и состоятельной. Статистическая оценка вычисленное по данным выборки и зависящее только от них. Чтобы оценка давала хорошее приближение, она должна быть несмещенной, эффективной и состоятельной. Статистическая оценка  параметра параметра  называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть  Оценка Оценка  называется эффективной, если при данном объеме выборки называется эффективной, если при данном объеме выборки  она имеет наименьшую дисперсию. Оценка она имеет наименьшую дисперсию. Оценка  называется состоятельной, если при называется состоятельной, если при  она стремится по вероятности к оцениваемому параметру она стремится по вероятности к оцениваемому параметру  то есть при любом то есть при любом  предел предел  Это означает, что с увеличением объема выборки мы все ближе приближаемся к оцениваемому параметру Это означает, что с увеличением объема выборки мы все ближе приближаемся к оцениваемому параметру  то есть практически достоверно то есть практически достоверно  Заметим, что состоятельность оценки обязательна для любого правила оценивания (несостоятельные оценки не используются). Точечной называют оценку, которая определяется одним числом. Например, рассмотренные в п. VI оценки неизвестных параметров нормального распределения: выборочное среднее Заметим, что состоятельность оценки обязательна для любого правила оценивания (несостоятельные оценки не используются). Точечной называют оценку, которая определяется одним числом. Например, рассмотренные в п. VI оценки неизвестных параметров нормального распределения: выборочное среднее  , исправленные выборочные дисперсия , исправленные выборочные дисперсия  и среднее квадратическое отклонение и среднее квадратическое отклонение  , являются точечными. Точечные оценки неизвестного параметра , являются точечными. Точечные оценки неизвестного параметра  хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестно с какой точностью они дают оцениваемый параметр. При малых объемах выборки точечные оценки могут значительно отличаться от оцениваемого параметра. Кроме того, при решении практических задач часто требуется определить и надежность этих оценок. Тогда и возникает задача о приближении параметра хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестно с какой точностью они дают оцениваемый параметр. При малых объемах выборки точечные оценки могут значительно отличаться от оцениваемого параметра. Кроме того, при решении практических задач часто требуется определить и надежность этих оценок. Тогда и возникает задача о приближении параметра  не одним числом, а целым интервалом не одним числом, а целым интервалом  В этой связи, наряду с точечными оценками пользуются еще и интервальными, которые определяются двумя числами — концами интервала. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал В этой связи, наряду с точечными оценками пользуются еще и интервальными, которые определяются двумя числами — концами интервала. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал  внутри которого с заранее выбранной вероятностью внутри которого с заранее выбранной вероятностью  находится точное значение оцениваемого параметра находится точное значение оцениваемого параметра 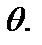 Интервал Интервал  покрывающий с вероятностью покрывающий с вероятностью  истинное значение параметра истинное значение параметра  называется доверительным интервалом,а вероятность называется доверительным интервалом,а вероятность  — доверительной вероятностью или надежностью оценки. Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно несмещенной точечной оценки — доверительной вероятностью или надежностью оценки. Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно несмещенной точечной оценки  то есть интервал вида то есть интервал вида  такой, что такой, что  Число Число  характеризует точность оценки: чем меньше разность характеризует точность оценки: чем меньше разность  , тем точнее оценка. Обычно надежность оценки , тем точнее оценка. Обычно надежность оценки  выбирается заранее и зависит от конкретно решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, очевидно, должна быть выше степени доверия покупателя к надежности телевизора, игрушки и т.д. Обычно доверительную вероятность выбирается заранее и зависит от конкретно решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, очевидно, должна быть выше степени доверия покупателя к надежности телевизора, игрушки и т.д. Обычно доверительную вероятность  берут равной 0,9, 0,95, 0,99 или 0,999. Разность берут равной 0,9, 0,95, 0,99 или 0,999. Разность  показывает, с какой вероятностью заключение о надежности оценки ошибочно, и называется уровнем значимости. В зависимости от конкретного случая уровень значимости показывает, с какой вероятностью заключение о надежности оценки ошибочно, и называется уровнем значимости. В зависимости от конкретного случая уровень значимости  принимают равным 0,1, 0,05, 0,01 или 0,001. принимают равным 0,1, 0,05, 0,01 или 0,001.
28. Доверительный интервал для оценки математического ожидания нормального распределения (t-распределение Стьюдента). Доверительный интервал для математического ожидания  при неизвестном среднем квадратическом отклонении при неизвестном среднем квадратическом отклонении  нормально распределенного признака определяется из двойного неравенства нормально распределенного признака определяется из двойного неравенства (27),где (27),где  — исправленное среднее квадратическое отклонение, значение параметра — исправленное среднее квадратическое отклонение, значение параметра  определяется по таблице приложения 3 критических точек распределения Стьюдента[2] по заданной доверительной вероятности определяется по таблице приложения 3 критических точек распределения Стьюдента[2] по заданной доверительной вероятности 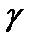 (или уровню значимости (или уровню значимости 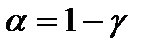 ) и числу степеней свободы ) и числу степеней свободы  . Отметим, что при больших выборках (объема . Отметим, что при больших выборках (объема  ) ) 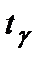 и число и число  , найденное по таблице значений функции Лапласа, практически совпадают.Доверительный интервал для математического ожидания , найденное по таблице значений функции Лапласа, практически совпадают.Доверительный интервал для математического ожидания  при известном среднем квадратическом отклонении при известном среднем квадратическом отклонении  нормально распределенного признака определяется из двойного неравенства нормально распределенного признака определяется из двойного неравенства (26),где (26),где  — объем выборки, — объем выборки,  — выборочное среднее, — выборочное среднее,  — аргумент функции Лапласа — аргумент функции Лапласа 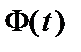 , при котором , при котором  — определяется при заданной надежности — определяется при заданной надежности  по таблице приложения 2 значений функции Лапласа. по таблице приложения 2 значений функции Лапласа.
|

 по данным выборки. Статистической оценкой неизвестного параметра
по данным выборки. Статистической оценкой неизвестного параметра  генеральной совокупности называется его приближенное значение
генеральной совокупности называется его приближенное значение  вычисленное по данным выборки и зависящее только от них. Чтобы оценка давала хорошее приближение, она должна быть несмещенной, эффективной и состоятельной. Статистическая оценка
вычисленное по данным выборки и зависящее только от них. Чтобы оценка давала хорошее приближение, она должна быть несмещенной, эффективной и состоятельной. Статистическая оценка  параметра
параметра  называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть
называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть  Оценка
Оценка  называется эффективной, если при данном объеме выборки
называется эффективной, если при данном объеме выборки  она имеет наименьшую дисперсию. Оценка
она имеет наименьшую дисперсию. Оценка  называется состоятельной, если при
называется состоятельной, если при  она стремится по вероятности к оцениваемому параметру
она стремится по вероятности к оцениваемому параметру  то есть при любом
то есть при любом  предел
предел  Это означает, что с увеличением объема выборки мы все ближе приближаемся к оцениваемому параметру
Это означает, что с увеличением объема выборки мы все ближе приближаемся к оцениваемому параметру  то есть практически достоверно
то есть практически достоверно  Заметим, что состоятельность оценки обязательна для любого правила оценивания (несостоятельные оценки не используются). Точечной называют оценку, которая определяется одним числом. Например, рассмотренные в п. VI оценки неизвестных параметров нормального распределения: выборочное среднее
Заметим, что состоятельность оценки обязательна для любого правила оценивания (несостоятельные оценки не используются). Точечной называют оценку, которая определяется одним числом. Например, рассмотренные в п. VI оценки неизвестных параметров нормального распределения: выборочное среднее  , исправленные выборочные дисперсия
, исправленные выборочные дисперсия  и среднее квадратическое отклонение
и среднее квадратическое отклонение  , являются точечными. Точечные оценки неизвестного параметра
, являются точечными. Точечные оценки неизвестного параметра  хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестно с какой точностью они дают оцениваемый параметр. При малых объемах выборки точечные оценки могут значительно отличаться от оцениваемого параметра. Кроме того, при решении практических задач часто требуется определить и надежность этих оценок. Тогда и возникает задача о приближении параметра
хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестно с какой точностью они дают оцениваемый параметр. При малых объемах выборки точечные оценки могут значительно отличаться от оцениваемого параметра. Кроме того, при решении практических задач часто требуется определить и надежность этих оценок. Тогда и возникает задача о приближении параметра  В этой связи, наряду с точечными оценками пользуются еще и интервальными, которые определяются двумя числами — концами интервала. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал
В этой связи, наряду с точечными оценками пользуются еще и интервальными, которые определяются двумя числами — концами интервала. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал  внутри которого с заранее выбранной вероятностью
внутри которого с заранее выбранной вероятностью  находится точное значение оцениваемого параметра
находится точное значение оцениваемого параметра 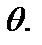 Интервал
Интервал  покрывающий с вероятностью
покрывающий с вероятностью  истинное значение параметра
истинное значение параметра  называется доверительным интервалом,а вероятность
называется доверительным интервалом,а вероятность  — доверительной вероятностью или надежностью оценки. Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно несмещенной точечной оценки
— доверительной вероятностью или надежностью оценки. Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно несмещенной точечной оценки  то есть интервал вида
то есть интервал вида  такой, что
такой, что  Число
Число  характеризует точность оценки: чем меньше разность
характеризует точность оценки: чем меньше разность  , тем точнее оценка. Обычно надежность оценки
, тем точнее оценка. Обычно надежность оценки  выбирается заранее и зависит от конкретно решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, очевидно, должна быть выше степени доверия покупателя к надежности телевизора, игрушки и т.д. Обычно доверительную вероятность
выбирается заранее и зависит от конкретно решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, очевидно, должна быть выше степени доверия покупателя к надежности телевизора, игрушки и т.д. Обычно доверительную вероятность  берут равной 0,9, 0,95, 0,99 или 0,999. Разность
берут равной 0,9, 0,95, 0,99 или 0,999. Разность  показывает, с какой вероятностью заключение о надежности оценки ошибочно, и называется уровнем значимости. В зависимости от конкретного случая уровень значимости
показывает, с какой вероятностью заключение о надежности оценки ошибочно, и называется уровнем значимости. В зависимости от конкретного случая уровень значимости  принимают равным 0,1, 0,05, 0,01 или 0,001.
принимают равным 0,1, 0,05, 0,01 или 0,001. при неизвестном среднем квадратическом отклонении
при неизвестном среднем квадратическом отклонении  нормально распределенного признака определяется из двойного неравенства
нормально распределенного признака определяется из двойного неравенства (27),где
(27),где  определяется по таблице приложения 3 критических точек распределения Стьюдента[2] по заданной доверительной вероятности
определяется по таблице приложения 3 критических точек распределения Стьюдента[2] по заданной доверительной вероятности 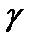 (или уровню значимости
(или уровню значимости 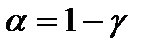 ) и числу степеней свободы
) и числу степеней свободы  . Отметим, что при больших выборках (объема
. Отметим, что при больших выборках (объема  )
) 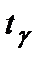 и число
и число  , найденное по таблице значений функции Лапласа, практически совпадают.Доверительный интервал для математического ожидания
, найденное по таблице значений функции Лапласа, практически совпадают.Доверительный интервал для математического ожидания  при известном среднем квадратическом отклонении
при известном среднем квадратическом отклонении  (26),где
(26),где  — объем выборки,
— объем выборки,  — выборочное среднее,
— выборочное среднее,  — аргумент функции Лапласа
— аргумент функции Лапласа 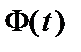 , при котором
, при котором  — определяется при заданной надежности
— определяется при заданной надежности  по таблице приложения 2 значений функции Лапласа.
по таблице приложения 2 значений функции Лапласа.