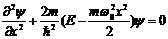Прохождение частицы через потенциальный барьер. Туннельный эффект.

Рассмотрим простейший потенциальный барьер прямоугольной формы. Для одномерного (по оси х) движения частицы.

        ì∞,x<0 (для области 1)

U(x)=í0,0≤x≤l (для области 2)         

     î0,x>1 (для области 3)  

где l-ширина ямы, а энергия отсчитывается от ее дна, U-высота. Частица, обладая энергией Е, либо беспрепятственно пройдет над барьером( при Е>U), либо отразится от него (при Е<U) и будет двигаться в обратную сторону. Для микрочастица, даже при Е>U, имеется вероятность отражения от барьера, и при Е<U есть вероятность проникновения через барьер. Это слудет из решения ур-ния Шредингера, описывающего движение микрочастицы

для областей 1 и 3 k²=2mE/h² ; для области 2 q²=2m(E-U)/h²

Общие решения этих диф.уравнений:

Ψ₁(x)=A₁e^ikx+B₁e^-ikx(для области 1);Ψ₂(x)=A₂e^iqx+B₂e^-iqx(для области2) Ψ₃(x)=A₃e^ikx+B₃e^-ikx(для области 3).

В частности, для области 1 полная волновая, будет иметь вид ψ₁(x,t)=ψ₁(x)e^-(i/h)Et=A₁e^{-(i/h)(Et-px)}+B₁x^{-(i/h)(Et+px)} ( в этом выражении первый член представляет собой плоскую волну вдоль х, другой – волну, распространяющаяся в обратную сторону). В области 3 есть только прошедшая сквозь барьер волна и поэтому В₃=0.Для области 2 q=iβ;β=√2m(E-U) /h.

Получили Ψ₁(x)=A₁e^ikx+B₁e^-ikx, Ψ₂(x)=A₂e^-βx+B₂e^βx ,Ψ₃(x)=A₃e^ikx

Качественный характер функций ψ₁(х),ψ₂(х),ψ₃(х)(см.рис2), откуда следует, что волновая функция не равна нулю и внутри барьера, а в области3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой. Т.о. приходим к явлению – туннельный эффект, когда микрочастица может пройти сквозь потенциальный барьер.

15.Уравнение Шредингера для гармонического осциллятора и анализ его решений.

Линейный гармонический осциллятор – система, совершающая одномерное движение под действием квазиупругой силы – является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов. Потенциальная энергия осциллятора равна

U=mω₀²x²/2 где ω₀- собственная частота осциллятора,m- масса частицы.

Гармонический осциллятор в квантовой механике – квантовый осциллятор – описывается уравнением Шредингера, учитывающим выражение для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются ур-нием Шредингера вида

где Е- полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что это уравнение решается только при собственных значениях энергии E_n=(n+½)ħω₀. Эта формула показывает, что энергия квантового осциллятора может иметь только дискретные значения, т.е. квантуется. Строгое решение задачи о квантовом осцилляторе приводит еще к отличию от классического рассмотрения. Квантово-механический расчет показывает, что частицу можно обнаружить за пределами дозволенной области, в то время как с классической точки зрения она не может выйти за пределы области. Т.о. имеется отличная от нуля вероятность обнаружить частицу в области, которая является классически запрещенной.

16, 17.Представление физических величин операторами. Вычисление средних значений физических величин.

 А) Оператор координаты. Действие сводится к умножению волновой функции на эту координату: x^{^}y=xy, y^y=yy, z^y=zy или x^=x…

б) Оператор проекций импульса. Выражаются с помощью операторов дифференцирования по соответствующим координатам: P^_x=(h/i)(¶/¶x), P^_y=(h/i)(¶/¶y), P^_z=(h/i)(¶/¶z),­­­­­­`p^={ P^_x, P^_y, P^_z}.

В) Оператор момента импульса:`

L=`r´`p, L_x=yp_z-zp_y; L_y=zp_y-xp_z; L_z=xp_y-yp_x;

L^_x=y^p^_z-z^p^_y=(h/i)(y¶/¶x-z¶/¶y).

 Г) Оператор кинетической энергии. Определим T, пользуясь формулой Т=p²/2m, T^=p^²/2m=-h²/2m. Вычисление средних значений: L^y=Ly,<L>=òy*L^ydV, y(r)=Aexp(-r/a)