Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Корни характеристического уравения - вещественные и равные ⇐ ПредыдущаяСтр 3 из 3 То есть,
Пример 3. Решить линейное однородное дифференциальное уравнение
Решение. Характеристическое уравнение
Нет времени вникать в решение? Можно заказать работу! Пример 4. Решить линейное однородное дифференциальное уравнение
Решение. Характеристическое уравнение
Корни характеристического уравнения - комплексные То есть,
Пример 5. Решить линейное однородное дифференциальное уравнение
Решение. Характеристическое уравнение
Пример 6. Решить линейное однородное дифференциальное уравнение
Решение. Характеристическое уравнение
Важное замечание. Теория решения линейных дифференциальных уравнений второго порядка гласит, что вышеприведённые общие решения уравнения получаются тогда, когда Линейную независимость решений можно проверить с помощью определителя Вронского: 
Если определитель Вронского не равен нулю, то решения - линейно независимые. Во всех приведённых выше примерах получены линейно независимые решения.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 236. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
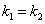 . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
. В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид .
. .
. имеет равные корни
имеет равные корни 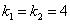 . Соответствующие частные решения уравнения:
. Соответствующие частные решения уравнения:  и
и  . Общее решение данного дифференциального уравения имеет вид
. Общее решение данного дифференциального уравения имеет вид
 .
. имеет равные корни
имеет равные корни  . Соответствующие частные решения уравнения:
. Соответствующие частные решения уравнения:  и
и  . Общее решение данного дифференциального уравения имеет вид
. Общее решение данного дифференциального уравения имеет вид .
.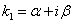 ,
, 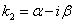 ,
,  . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
. В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид .
. .
. имеет комплексные корни
имеет комплексные корни  и
и  . Соответственно
. Соответственно  и
и  . Общее решение данного дифференциального уравения имеет вид
. Общее решение данного дифференциального уравения имеет вид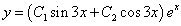 .
. .
. имеет комплексные корни
имеет комплексные корни 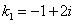 и
и  . Соответственно
. Соответственно 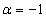 и
и  . Общее решение данного дифференциального уравения имеет вид
. Общее решение данного дифференциального уравения имеет вид .
.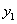 и
и  - какие-либо два линейно независимых частных решения уравнения.
- какие-либо два линейно независимых частных решения уравнения. .
.