
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные однородные дифференциальные уравнения 1 -го порядка;.
Однородные дифференциальные уравнения (корни характеристического уравнения действительные и различные). Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида  y'' + py' + qy = 0, где p и q - постоянные величины. На то, что это уравнение второго порядка, указывает наличие второй производной от искомой функции, а на его однородность - нуль в правой части. Постоянными коэффициентами называются уже упомянутые выше величины. Чтобы решить линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, нужно сначала решить так называемое характеристическое уравнение вида k² + pq + q = 0, которое, как видно, является обычным квадратным уравнением. В зависимости от решения характеристического уравнения возможны три различных варианта решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, которые сейчас разберём. Корни характеристического уравнения - действительные и различные Иными словами,
Пример 1. Решить линейное однородное дифференциальное уравнение
Решение. Характеристическое уравнение имеет вид
Пример 2. Решить линейное однородное дифференциальное уравнение
Решение. Характеристическое уравнение имеет вид
|
|||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 190. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |




 (3.9)
Линейным оно называется потому, что и неизвестная функция
(3.9)
Линейным оно называется потому, что и неизвестная функция 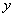 , и её производная
, и её производная  входят в это уравнение линейно (в первой степени) - аналогично тому, как входят
входят в это уравнение линейно (в первой степени) - аналогично тому, как входят  и
и  . А добавка «однородное» связана с тем, что правая часть уравнения (3.9) представляет собой нуль. Если же там будет не нуль, то такое уравнение будет называться линейным неоднородным (его решению посвящён следующий пункт 5).
Уравнение (3.9) является заодно и уравнением с разделяющимся переменными вида (3.3) при
. А добавка «однородное» связана с тем, что правая часть уравнения (3.9) представляет собой нуль. Если же там будет не нуль, то такое уравнение будет называться линейным неоднородным (его решению посвящён следующий пункт 5).
Уравнение (3.9) является заодно и уравнением с разделяющимся переменными вида (3.3) при  и
и 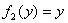 . Из этого следует схема его решения:
1)
. Из этого следует схема его решения:
1)  . Таким образом, одно частное решение уравнения (3.9) (тривиальное решение) мы уже имеем: это функция
. Таким образом, одно частное решение уравнения (3.9) (тривиальное решение) мы уже имеем: это функция 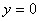 .
2) Найдем общее решение уравнения (3.9):
.
2) Найдем общее решение уравнения (3.9):
 | разделяем переменные
| разделяем переменные 
 | интегрируем обе части |
| интегрируем обе части | 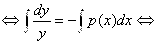

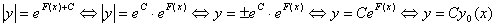 (3.10)
Итак, общее решение уравнения (3.9) имеет вид
(3.10)
Итак, общее решение уравнения (3.9) имеет вид  , где
, где  - одно из частных решений этого уравнения (оно выделяется из общего решения, если положить в нем С=1). Заметим, что и тривиальное решение
- одно из частных решений этого уравнения (оно выделяется из общего решения, если положить в нем С=1). Заметим, что и тривиальное решение  Этого уравнения. После этого по формуле (3.11) можно записать и его общее решение.
Этого уравнения. После этого по формуле (3.11) можно записать и его общее решение.
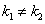 . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
. В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид .
. .
.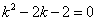 , его корни
, его корни  и
и  - вещественные и различные. Соответствующие частные решения уравнения:
- вещественные и различные. Соответствующие частные решения уравнения:  и
и  . Общее решение данного дифференциального уравения имеет вид
. Общее решение данного дифференциального уравения имеет вид .
. .
. , его корни
, его корни 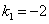 и
и  - вещественные и различные. Соответствующие частные решения уравнения:
- вещественные и различные. Соответствующие частные решения уравнения:  и
и  . Общее решение данного дифференциального уравения имеет вид
. Общее решение данного дифференциального уравения имеет вид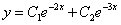 .
.