
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Применение определенного интеграла для нахождения площадей различных фигур.Стр 1 из 3Следующая ⇒ На этом уроке будем учиться вычислять площади плоских фигур, которые ограничены осью абсцисс (Ox), отрезками прямых x = a, x = b и графиком непрерывной и неотрицательной функции y = f(x) для значений "икса", принадлежащих отрезку [a, b]. Такая фигура называется криволинейной трапецией. Боковые отрезки могут вырождаться в точки. Площадь s этой криволинейной трапеции может быть вычислена по формуле
Итак, определённый интеграл от неотрицательной непрерывной функции f(x) по [a, b] (график функции расположен выше оси Ox) численно равен площади криволинейной трапеции с основанием [a, b], ограниченной сверху графиком функции y = f(x). В этом заключается геометрический смысл определённого интеграла. Рисунки таких фигур - в примерах. Если же f(x) ≤ 0 (график функции расположен ниже оси Ox), то площадь криволинейной трапеции может быть вычислена по формуле
Есть ещё случаи, когда и верхняя, и нижняя границы фигуры - функции, соответственно y = f(x) и y = φ(x), то площадь такой фигуры вычисляется по формуле
Таким образом, вычисление площадей плоских фигур - одна из важнейших прикладных задач, в которой определённый интеграл находит наиболее плодотворное применение. Все мы изучали сведения из элементарной геометрии, которые позволяют вычислять площади прямолинейных фигур - прямоугольников, треугольников и многоугольников. Что же касается криволинейных фигур, то здесь для нахождения площади средств из элементарной геометрии уже недостаточно. Итак, к делу. Учимся применять то, что изложено в самом верху этой статьи. Начнём со случаев, когда площадь фигуры может быть вычислена по формуле (1).  Пример 1.Найти площадь фигуры, ограниченной графиком функции
Решение. Так как y = 1/x > 0 на отрезке [1; 3], то площадь криволинейной трапеции находим по формуле (1):
Пример 2.Найти площадь фигуры, ограниченной графиком функции
Решение. Результат применения формулы (1):
Если Пример 3.Найти площадь фигуры, ограниченной графиком функции
Решение. Фигура, соответствующая условию задачи - криволинейная трапеция, у которой левый отрезок выродился в точку. Пределами интегрирования служат 0 и 4. Поскольку
Пример 4.Найти площадь фигуры, ограниченной линиями
Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры, заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной трапеции ABC. При вычислении площади треугольника OABпределами интегрирования служат абсциссы точек O и A, а для фигуры ABC - абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C - точкой пересечения параболы с осью Ox). Решая совместно (как систему) уравнения прямой и параболы, получим
Пример 5.Найти площадь криволинейной трапеции ACDB, если уравнение кривой CD
Решение. Выразим данное уравнение кривой через игрек:
Нет времени вникать в решение? Можно заказать работу! Переходим к случаям, когда площадь фигуры может быть вычислена по формуле (2). Пример 6.Найти площадь фигуры, ограниченной параболой
Решение. Данная фигура расположена ниже оси абсцисс. Поэтому для вычисления её площади воспользуемся формулой (2). Пределами интегрирования являются абсциссы
Пример 7.Найти площадь, заключённую между осью абсцисс (Ox) и двумя соседними волнами синусоиды.
Решение. Площадь данной фигуры можем найти по формуле (2):
Найдём отдельно каждое слагаемое:
Окончательно находим площадь:
Пример 8.Найти площадь фигуры, заключённой между параболой
Решение. Выразим уравнения линий через игрек:
Площадь по формуле (2) получим как
где a и b - абсциссы точек A и B. Найдём их, решая совместно уравнения:
Отсюда
Окончательно находим площадь:
И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3). Первый из этих примеров предлагается решить самостоятельно, а затем можно посмотреть правильное решение. Пример 9.Найти площадь фигуры, ограниченной графиками функций Посмотреть правильное решение и ответ. Пример 10.Найти площадь фигуры, ограниченной графиками функций
Решение. Так как
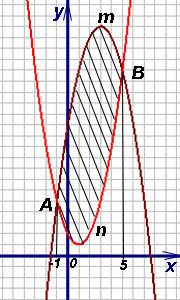
Пример 11.Найти площадь фигуры, заключённой между параболами
Решение. Требуется вычислить площадь фигуры AmBn, у которой боковые отрезки выродились в точки A и B пересечения парабол. Решая совместно (как систему) уравнения парабол, находим их абсциссы:
Пример 12.Найти площадь фигуры, заключённой между параболой
Решение. Находим абсциссы точек пересечения параболы и прямой:
37.Понятие о дифференциальных уравнениях. Их виды.
Вот примеры ОДУ первого, второго и пятого порядков соответственно В качестве примеров уравнений в частных производных второго порядка приведем Далее мы будем рассматривать только обыкновенные дифференциальные уравнения n-ого порядка вида Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Решение дифференциального уравнения - это неявно заданная функция Ф(x, y) = 0 (в некоторых случаях функцию y можно выразить через аргумент x явно), которая обращает дифференциальное уравнение в тождество. ОБРАТИТЕ ВНИМАНИЕ. Решение дифференциального уравнения всегда ищется на заранее заданном интервале X. Почему мы об этом говорим отдельно? Да потому что в условиях многих задач об интервале X не упоминают. То есть, обычно условие задач формулируется так: «найдите решение обыкновенного дифференциального уравнения Решение дифференциального уравнения часто называют интегралом дифференциального уравнения. Функции Одним из решений дифференциального уравнения Общее решение дифференциального уравнения – это множество решений, содержащее все без исключения решения этого дифференциального уравнения. Общее решение дифференциального уравнения еще называют общим интегралом дифференциального уравнения. Вернемся к примеру. Общее решение дифференциального уравнения Если решение дифференциального уравнения удовлетворяет изначально заданным дополнительным условиям, то его называют частным решением дифференциального уравнения. Частным решением дифференциального уравнения
38. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальные уравнения с разделенными переменными Дифференциальные уравнения Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него. Будем считать, что функции f(y) и g(x) непрерывны. Общим интегралом уравнения с разделенными переменными является равенство Пример. Найдите общее решение дифференциального уравнения с разделенными переменными Решение. Проинтегрируем обе части равенства: Мы пришли к неявно заданной функции Замечание. Ответ можно записать в любом из трех видов Дифференциальные уравнения с разделяющимися переменными Прежде чем продолжить, напомним, что В дифференциальных уравнениях При разделении переменных следует быть очень внимательными, чтобы проводимые преобразования были эквивалентными (чтобы f2(y) и g1(x) не обращались в ноль на интервале интегрирования). В противном случае можно потерять некоторые решения. Разберемся с этим на примере. Пример. Найти все решения дифференциального уравнения Решение. Это уравнение с разделяющимися переменными, так как мы можем разделить xи y: Для нулевой функции y исходное уравнение обращается в тождество Проинтегрируем дифференциальное уравнение с разделенными переменными В преобразованиях мы заменили C2 - C1 на С. Мы получили решение ДУ в виде неявно заданной функции Ответ:
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 263. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1).
(1). . (2)
. (2) . (3)
. (3) , осью абсцисс (Ox) и прямыми x = 1, x = 3.
, осью абсцисс (Ox) и прямыми x = 1, x = 3.
 .
. , прямой x = 1 и осью абсцисс (Ox).
, прямой x = 1 и осью абсцисс (Ox).

 то s = 1/2; если
то s = 1/2; если  то s = 1/3, и т.д.
то s = 1/3, и т.д. , осью абсцисс (Ox) и прямой x = 4.
, осью абсцисс (Ox) и прямой x = 4.
 , по формуле (1) находим площадь криволинейной трапеции:
, по формуле (1) находим площадь криволинейной трапеции: .
.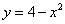 ,
,  ,
,  и находящейся в 1-й четверти.
и находящейся в 1-й четверти.
 (абсциссу точки A) и
(абсциссу точки A) и  (абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим
(абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим 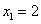 ,
,  (абсциссы точек C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:
(абсциссы точек C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:
 и абсциссы A и B соответственно 1 и 2.
и абсциссы A и B соответственно 1 и 2.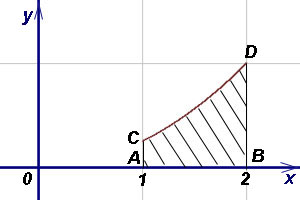
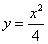 Площадь криволинейной трапеции находим по формуле (1):
Площадь криволинейной трапеции находим по формуле (1): .
.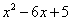 и осью абсцисс (Ox).
и осью абсцисс (Ox).
 точек пересечения параболы с осью Ox. Следовательно,
точек пересечения параболы с осью Ox. Следовательно,

 .
. .
. .
. .
. .
.

 ,
,


 и
и  .
. ,
,  и прямыми
и прямыми  и
и 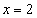 .
.
 на отрезке [0, 2], то, используя для нахождения площади формулу (3), получим
на отрезке [0, 2], то, используя для нахождения площади формулу (3), получим

 и
и 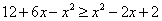 . Следовательно, по формуле (3) находим площадь фигуры:
. Следовательно, по формуле (3) находим площадь фигуры:
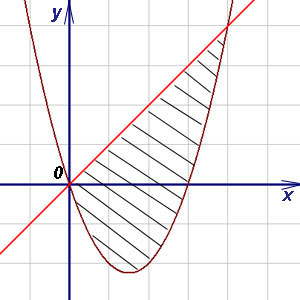
 и прямой
и прямой  .
.
 и
и  . Так как
. Так как 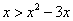 на отрезке [0, 4], то по формуле (3) находим площадь фигуры:
на отрезке [0, 4], то по формуле (3) находим площадь фигуры:



 или
или  , где Ф(x, y) = 0 неизвестная функция, заданная неявно (когда возможно, будем ее записывать в явном представлении y = f(x)).
, где Ф(x, y) = 0 неизвестная функция, заданная неявно (когда возможно, будем ее записывать в явном представлении y = f(x)). или
или  можно назвать решением дифференциального уравнения
можно назвать решением дифференциального уравнения 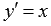 .
. является функция
является функция  . Действительно, подставив эту функцию в исходное уравнение, получим тождество
. Действительно, подставив эту функцию в исходное уравнение, получим тождество  . Несложно заметить, что другим решением этого ОДУ является, например,
. Несложно заметить, что другим решением этого ОДУ является, например,  . Таким образом, дифференциальные уравнения могут иметь множество решений.
. Таким образом, дифференциальные уравнения могут иметь множество решений.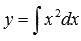 или
или  , где C – произвольная постоянная. Выше мы указали два решения этого ОДУ, которые получаются из общего интеграла дифференциального уравнения
, где C – произвольная постоянная. Выше мы указали два решения этого ОДУ, которые получаются из общего интеграла дифференциального уравнения 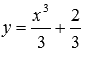 . Действительно,
. Действительно,  и
и  .
.
 .
. . Если интегралы из этого равенства выражаются в элементарных функциях, то мы можем получить общее решение дифференциального уравнения как неявно заданную функцию Ф(x, y) = 0, а иногда получается выразить функцию y в явном виде.
. Если интегралы из этого равенства выражаются в элементарных функциях, то мы можем получить общее решение дифференциального уравнения как неявно заданную функцию Ф(x, y) = 0, а иногда получается выразить функцию y в явном виде. .
. . По сути, мы уже получили общее решение исходного дифференциального уравнения, так как свели задачу решения дифференциального уравнения к уже известной задаче нахождения неопределенных интегралов. Однако, эти неопределенные интегралы выражаются в элементарных функциях, и мы можем взять их, используя таблицу первообразных:
. По сути, мы уже получили общее решение исходного дифференциального уравнения, так как свели задачу решения дифференциального уравнения к уже известной задаче нахождения неопределенных интегралов. Однако, эти неопределенные интегралы выражаются в элементарных функциях, и мы можем взять их, используя таблицу первообразных:
 , которая является общим решением исходного дифференциального уравнения с разделенными переменными. Ответ можно оставить в таком виде. Но в нашем случае искомую функцию y можно выразить явно через аргумент x. Итак,
, которая является общим решением исходного дифференциального уравнения с разделенными переменными. Ответ можно оставить в таком виде. Но в нашем случае искомую функцию y можно выразить явно через аргумент x. Итак,  , где
, где  . То есть, функция
. То есть, функция  является общим решением исходного дифференциального уравнения.
является общим решением исходного дифференциального уравнения. .
. когда y является функцией аргумента x.
когда y является функцией аргумента x. переменные могут быть разделены, проведением преобразований. Такие ОДУ называются дифференциальными уравнениями с разделяющимися переменными. Соответствующее ДУ с разделенными переменными запишется как
переменные могут быть разделены, проведением преобразований. Такие ОДУ называются дифференциальными уравнениями с разделяющимися переменными. Соответствующее ДУ с разделенными переменными запишется как  .
. .
.
 , поэтому, y = 0 является решением дифференциального уравнения. Это решение мы могли упустить из виду.
, поэтому, y = 0 является решением дифференциального уравнения. Это решение мы могли упустить из виду. :
:
 . На этом можно закончить. Однако в нашем случае функцию y можно выразить явно, проведя потенцирование полученного равенства:
. На этом можно закончить. Однако в нашем случае функцию y можно выразить явно, проведя потенцирование полученного равенства:
 .
.