
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интегралы, сводящиеся к интегрированию рациональных дробей. ⇐ ПредыдущаяСтр 4 из 4 Рациональной функцией
Интегралы вида Данный интеграл сводится к интегрированию рациональных дробей заменой переменной После подстановки получаем Полученное выражение является рациональной дробью.
Задача. Найти Сделаем замену переменной После подстановки получаем Выражение, стоящее под знаком интеграла, является правильной рациональной дробью. Представление этой дроби в виде суммы простейших дробей ищем в виде
Осталось определить неизвестные пока коэффициенты А, В, С. Приведем правую часть к общему знаменателю, который равен
В полученном соотношении приравниваем коэффициенты при одинаковых степенях
Решая эту систему уравнений, находим коэффициенты.
Тогда Подставляя
Найти Сделаем замену переменной После подстановки получаем
Выражение, стоящее под знаком интеграла, является правильной рациональной дробью. Представление этой дроби в виде суммы простейших дробей ищем в виде
Осталось определить неизвестные пока коэффициенты А, В, С. Приведем правую часть к общему знаменателю, который равен 
В полученном соотношении приравниваем коэффициенты при одинаковых степенях
Решая эту систему уравнений, находим коэффициенты.
Тогда
=
=
=
= Подставляя
Задача. Найти Сделаем замену переменной После подстановки получаем Выражение, стоящее под знаком интеграла, является правильной рациональной дробью. Представление этой дроби в виде суммы простейших дробей ищем в виде
Осталось определить неизвестные пока коэффициенты А, В, С. Приведем правую часть к общему знаменателю, который равен
В полученном соотношении приравниваем коэффициенты при одинаковых степенях
Решая эту систему уравнений, находим коэффициенты.
Тогда
Подставляя
Интегралы вида Данный неопределенный интеграл сводится к интегрированию рациональной дроби по следующей схеме. Обозначим через Сделаем замену переменной После указанной замены подынтегральное выражение превращается в рациональную дробь. Рассмотрим примеры. Задача. Найти Подынтегральная функция содержит Наименьшим целым числом, которое делится на 2 и на 3 является число 6. Сделаем замену
Тогда
Выражение, стоящее под знаком интеграла является неправильной рациональной дробью. Следовательно, его можно представить как сумму многочлена и правильной рациональной дроби.
Имеем
Следовательно
Подставляя
Задача. Найти Сделаем замену переменной
Подставляя
Интегралы вида Данный интеграл сводится к интегрированию рациональных дробей путем следующей замены (так называемая «универсальная тригонометрическая подстановка»). Обозначим Из школьного курса тригонометрии известны формулы выражения синуса и косинуса через тангенс половинного угла. На всякий случай мы напомним эти формулы. Итак:
Такая подстановка приводит вычисление исходного интеграла к интегрированию рациональной дроби. Задача. Найти Сделаем замену переменной
= Таким образом:
Задача. Найти Используя замену
То есть
Рассмотрим еще один класс интегралов – интегралы вида Поскольку
Задача. Найти Сначала убедимся, что данный интеграл действительно относится к указанному типу. Для этого преобразуем данное выражение
Выражение
После приведения к общему знаменателю в правой и левой частях получаем
Приравнивая коэффициенты при одинаковых степенях
Решая эту систему, получаем
Следовательно
= = = Получаем
Задача. Найти После замены переменной
= Следовательно
Тригонометрические подстановки в интегралах, содержащих выражения В этих случая полезны следующие подстановки. Для случая выражения Для случая выражения Для случая выражения Задача. Найти Сделаем замену Следовательно = Получаем
Задача. Найти Сделаем замену Следовательно = Получаем Найти Сделаем замену
Следовательно = Получаем
Интегралы вида Напомним некоторые формулы тригонометрии:
Задача. Найти Решение. =
Задача. Найти Решение. =
Задача. Найти Решение. =
Интегралы вида Рассмотрим два случая вычисления таких интегралов. Первый случай – это когда, по крайней мере, один из показателей степени Тогда = Полученное подынтегральное выражение является многочленом и его интегрирование не вызовет затруднений.
Задача. Найти Пусть Имеем =
Задача. Найти Пусть Имеем =
Второй случай – оба показателя степени В этом случае для понижения степени используются формулы
Задача. Найти Решение. = = = = = Таким образом Замечания: - при вычислении - при вычислении
Задача. Найти Решение. = = = Получаем
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 167. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 будем называть функцию, при вычислении которой используются следующие математические операции: сложение, вычитание, умножение, деление, возведение в целую степень.
будем называть функцию, при вычислении которой используются следующие математические операции: сложение, вычитание, умножение, деление, возведение в целую степень. .
. . Тогда
. Тогда  ,
,  .
. .
.

 .
. - знаменателю в левой части выражения, и приравняем числители в правой и левой частях. Получим
- знаменателю в левой части выражения, и приравняем числители в правой и левой частях. Получим .
.  и получаем систему уравнений для определения А, В, С.
и получаем систему уравнений для определения А, В, С.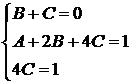 .
. .
.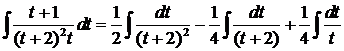 =
= 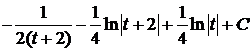
 , получаем
, получаем 
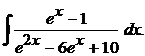

 .
.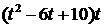 - знаменателю в левой части выражения, и приравняем числители в правой и левой частях. Получим
- знаменателю в левой части выражения, и приравняем числители в правой и левой частях. Получим .
.  .
. .
.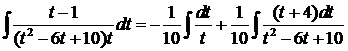 =
=


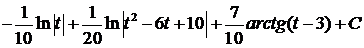
 =
=  .
.

 =.
=. - знаменателю в левой части выражения, и приравняем числители в правой и левой частях. Получим
- знаменателю в левой части выражения, и приравняем числители в правой и левой частях. Получим .
.  .
. .
. .
. .
. .
. - наименьшее общее кратное чисел
- наименьшее общее кратное чисел  . (На всякий случай напомним, что наименьшим общим кратным для некоторого множества целых чисел называется такое наименьшее целое число, которое делится без остатка на все числа данного множества.)
. (На всякий случай напомним, что наименьшим общим кратным для некоторого множества целых чисел называется такое наименьшее целое число, которое делится без остатка на все числа данного множества.) . Тогда
. Тогда  .
. .
. и
и  .
. ,
,  . Тогда
. Тогда  . Напомним, что
. Напомним, что . Следовательно
. Следовательно 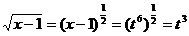 ,
, 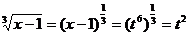 .
. .
.


 .
.
 . Тогда
. Тогда  ,
,  ,
,  . Тогда получаем
. Тогда получаем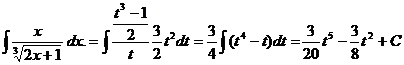 .
. .
. .
. . Тогда
. Тогда  ,
,  .
. .
. 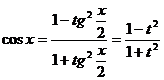 .
. .
.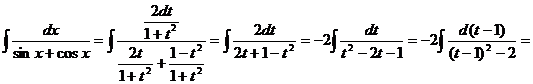
 .
. .
.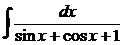 .
. .
. .
. .
. , то данный тип интегралов можно вычислять, используя универсальную тригонометрическую подстановку. Однако существует замена переменной, которая позволяет вычислить этот интеграл более просто. Такой заменой является
, то данный тип интегралов можно вычислять, используя универсальную тригонометрическую подстановку. Однако существует замена переменной, которая позволяет вычислить этот интеграл более просто. Такой заменой является  . Тогда
. Тогда  ,
,  . После такой подстановки вычисление интеграла сводится к интегрированию рациональной дроби.
. После такой подстановки вычисление интеграла сводится к интегрированию рациональной дроби. .
. .
. является правильной рациональной дробью и может быть разложено в сумму простейших рациональных дробей. Имеем
является правильной рациональной дробью и может быть разложено в сумму простейших рациональных дробей. Имеем
 .
. , получаем систему уравнений
, получаем систему уравнений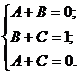
 .
.


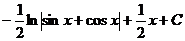 .
.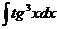

 .
. .
. ,
,  ,
,  .
.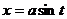 . Тогда
. Тогда 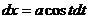 ,
, 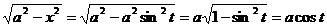 .
. . Тогда
. Тогда  ,
,  .
.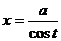 . Тогда
. Тогда  ,
,  .
. .
. . Тогда
. Тогда 
 .
.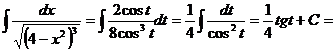
 .
.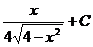 .
.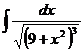 .
. . Тогда
. Тогда 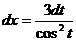 ,
,  .
.
 .
. .
. .
. . Тогда
. Тогда  ,
, .
.
 .
.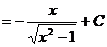 .
. .
. ;
; ;
; .
. .
.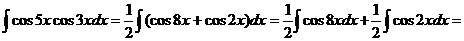
 .
. .
.
 .
. .
.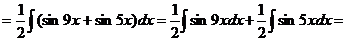
 .
. .
. или
или  является нечетным числом. Будем считать для определенности
является нечетным числом. Будем считать для определенности  . Обозначим
. Обозначим 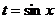 . Следовательно
. Следовательно  .
.
 .
. .
.

 .
. .
. . Тогда
. Тогда  .
.
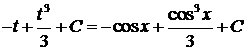 .
. ;
;  .
. .
.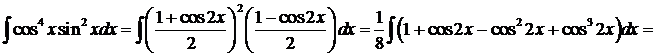
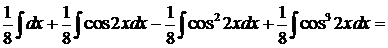



 .
. =
=  мы воспользовались формулой двойного угла
мы воспользовались формулой двойного угла  ;
; мы воспользовались правилом интегрирования в случае, когда, по крайне мере, одна из степеней нечетная.
мы воспользовались правилом интегрирования в случае, когда, по крайне мере, одна из степеней нечетная.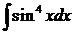 .
.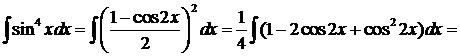


 .
. =
=