
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Использование замены переменнойСтр 1 из 4Следующая ⇒ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Московский государственный университет Приборостроения и информатики
Кафедра высшей математики Неопределенный интеграл (решение задач) Учебное пособие для студентов всех форм обучения для самостоятельной подготовки к выполнению контрольных работ.
Москва 2005
Составитель: к.ф.м.н., доцент Выборнов А.Н.. В пособии рассмотрены основные типы неопределенных интегралов и приведены методы их вычисления. Пособие составлено на основе пособия МГУПИ для заочного отделения (авторы: Баланкина Е.С., Головешкин В.А., Каримова Н.А., Меренкова Т.В., Соркина Л.И., Якобовская И.М.). Составителем переработано изложение теоретических положений и некоторых методов решения задач. Пособие может использоваться как дополнительное пособие по развитию навыков решения задач.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Прежде чем перейти к решению конкретных задач напомним некоторые понятия из теоретического курса. Функция Если некоторая функция Вся совокупность первообразных для функции Любая первообразная для данной функции  Принято писать Операция нахождения неопределенного интеграла называется интегрированием функции. Следовательно, проблема интегрирования функции сводится к нахождению некоторой конкретной первообразной. Отметим также, что можно очень просто проверить, правильно ли вычислен неопределенный интеграл. Для этого достаточно в выражении Прежде чем перейти к свойствам неопределенного интеграла, приведем таблицу некоторых основных интегралов от элементарных функций, которые мы в дальнейшем будем называть табличными интегралами.
Табличные интегралы. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Все решаемые в данном пособии задачи мы будем сводить к вычислению табличных интегралов.
Напомним некоторые свойства неопределенного интеграла. 1. Согласно определению неопределенного интеграла его производная равна подынтегральной функции, то есть
2. Дифференциал неопределенного интеграла равен подынтегральному выражению:
3.Неопределенный интеграл от производной некоторой функции равен этой функции плюс произвольная постоянная:
4. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:
Следующие свойства интегралов вытекает из соответствующих свойств производных.
5. Неопределенный интеграл от суммы (или разности) двух функций равен сумме (или, соответственно, разности) неопределенных интегралов от этих функций: .
6.Постоянный множитель можно выносить за знак неопределенного интеграла:
7. Из формулы производной произведения вытекает Формула интегрирования по частям:
8.Из формулы производной сложной функции вытекает формула: (Замена переменной в неопределенном интеграле ) Эту формулу используют как слева направо, так и справа налево. 1)справа налево: Например, пусть требуется вычислить
2)слева направо: Например, пусть нам известно, что
Рассмотрим примеры.
Использование замены переменной Задача. Найти Решение: Обозначим Подставляя в исходное выражение, получаем Иногда не вводят обозначение для новой переменной, а все выражение для новой переменной через старую используют как ее имя, записывая это выражение под знаком дифференциала. Это и называют «подведением под знак дифференциала». В рассмотренном примере:
Задача. Найти Решение: Обозначим Получаем
Задача. Найти Решение: Обозначим Получаем
Вычисление интегралов вида Метод вычисления таких интегралов изложим на примере: Задача. Найти Решение: Выделим полный квадрат в знаменателе:
Сделаем замену
В первом интеграле сделаем замену: Тогда Получаем:
Ответ:
Задача. Найти Ответ:
Задача. Найти
Ответ:
Вычисление интегралов вида Технология здесь аналогична рассмотренной в предыдущем случае. Задача.Найти Решение:
Выделим полный квадрат в подкоренном выражении в знаменателе: Получаем
В первом интеграле сделаем замену: Тогда
Ответ:
Задача. Найти Указание: Выделите полный квадрат в знаменателе:
Ответ:
|
|||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 181. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 называется первообразной для функции
называется первообразной для функции 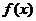 , если выполнено соотношение
, если выполнено соотношение  .
. , где С – произвольная постоянная, также будет первообразной для функции
, где С – произвольная постоянная, также будет первообразной для функции 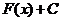 , где
, где  .
. .
. .
. (при
(при  ).
). .
.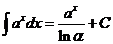 (
(  ), в частности
), в частности  .
. .
. .
.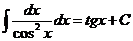 .
. .
. .
. .
. .
. .
. .
.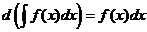 .
.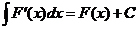 .
.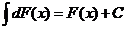 .
. .
. .
.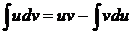

 , где
, где  - новая независимая переменная. Тогда
- новая независимая переменная. Тогда  . При этом, конечно, предполагаем, что после вычисления интеграла в правой части мы подставим вместо
. При этом, конечно, предполагаем, что после вычисления интеграла в правой части мы подставим вместо  из соотношения
из соотношения  должна быть обратима).
должна быть обратима). . Требуется вычислить интеграл вида
. Требуется вычислить интеграл вида 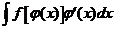 . Тогда
. Тогда 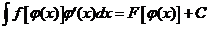 .
.
 . Тогда для дифференциала данной функции имеем выражение
. Тогда для дифференциала данной функции имеем выражение  . Следовательно
. Следовательно 
 .
. , мы можем записать
, мы можем записать  .
. .
.  . Тогда
. Тогда  . Следовательно,
. Следовательно, 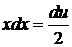 .
.
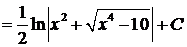 .
.
 . Тогда
. Тогда  . Следовательно,
. Следовательно, 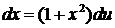 .
. .
. .
.
 .
. . Тогда
. Тогда  ,
,  .
.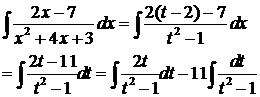
 .
. . Второй интеграл табличный.
. Второй интеграл табличный.

 .
.
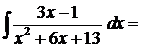
 .
.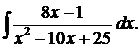
 =
= 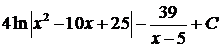 .
. .
. .
.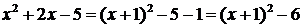 , сделаем замену
, сделаем замену  .
.
 .
. . Второй интеграл табличный.
. Второй интеграл табличный. .
. .
.

 .
.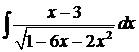
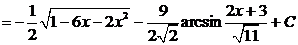 .
.