Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение параметров функциональной зависимости методом наименьших квадратовПри совместном исследовании двух случайных величин по имеющейся выборке (х1, у2), (х2, у2),…,(xk, yk) возникает задача определения зависимости между ними. Если вид функции y = f (x, a, b,...) задан, то требуется найти значения коэффициентов a, b,..., при которых yi наименее отличаются от f (xi). В методе наименьших квадратов коэффициенты должны быть такими, что а) Линейная зависимость y = ax + b. Если
б) Квадратичная зависимость y = (ax + b)2. Отсюда
в) Показательная зависимость
г) Зависимость вида
д) Логарифмическая зависимость y = ln(ax + b), то есть ey = ax + b, и
Пример 5. Найти параметры зависимости между х и у для выборки (Таблица 4): Таблица 4
для случаев: 1) линейной зависимости y = ax + b; 2) квадратичной зависимости y = (ax + b)2; 3) показательной зависимости y = eax + b. Определить, какая из функций является лучшим приближением зависимости между х и у. Решение. По виду выборки достаточно очевидно, что связь между х и у скорее всего не является линейной – у растет не пропорционально х. Проверим это предположение, найдя коэффициенты а и b для каждой из функций. Для этого вычислим предварительно
1)  2) у = (2,29х – 1,68)2. 3) у = е0,94х + 0,04. Вычислим значения (Таблица 5)
Таблица 5
Итак, наилучшим приближением является квадратичная функция.
ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ Линейная корреляция Если для выборки двумерной случайной величины (X, Y): {(xi, yi), i = 1, 2,..., n} вычислены выборочные средние
Напомним, что коэффициент корреляции – безразмерная величина, которая служит для оценки степени линейной зависимости между Х и Y: эта связь тем сильнее, чем ближе |r| к единице. Линейные уравнения, описывающие связь между Х и Y, называются выборочным уравнением прямой линии регрессии Y на Х:
и выборочным уравнением прямой линии регрессии Х на Y :
Пример 11. Для выборки двумерной случайной величины (Таблица 6) Таблица 6
вычислить выборочные средние, выборочные средние квадратические отклонения, выборочный коэффициент корреляции и составить выборочное уравнение прямой линии регрессии Y на Х. Решение.
Ранговая корреляция Рассмотрим выборку объема п, элементы которой обладают двумя качественными признаками: А и В (качественный признак невозможно измерить точно, но можно расположить объекты в порядке убывания или возрастания качества). Расположим элементы выборки в порядке ухудшения качества по признаку А. При этом зададим каждому объекту ранг хi, равный его порядковому номеру в последовательности объектов: xi = i. Затем расположим элементы выборки в порядке убывания качества по признаку В и присвоим каждому второй ранг: yi, где номер i – это номер объекта в первой последовательности рангов. Таким образом, получены две последовательности рангов: A: x1, x2, ..., xn B: y1, y2, ..., yn. Для исследования наличия связи между качественными признаками А и В можно использовать коэффициенты ранговой корреляции Спирмена и Кендалла. Коэффициент ранговой корреляции Спирмена вычисляется по формуле:
где di = xi – yi, n – объем выборки. Для вычисления коэффициента ранговой корреляции Кендалла найдем величины R1, R2, ..., Rn, где Ri – количество чисел, больших yi, стоящих справа от yi в последовательности рангов по признаку В. Тогда выборочный коэффициент ранговой корреляции Кендалла
где R = R1 + R2 + ... + Rn. Заметим, что оба коэффициента ранговой корреляции не превосходят по модулю единицы. При этом, чем ближе значение Пример 12. Десять школьников сдавали выпускной экзамен ЕГЭ по математике и вступительный экзамен по системе централизованного тестирования. Результаты обоих экзаменов оценивались по 100-балльной шкале и оказались следующими (1-я строка – оценки ЕГЭ, вторая – централизованного тестирования): 87 82 80 79 63 55 40 34 33 29 57 92 80 69 71 43 49 51 20 19 Найти выборочные коэффициенты корреляции Спирмена и Кендалла. Решение. Составим последовательности рангов по убыванию баллов на каждом экзамене: xi 1 2 3 4 5 6 7 8 9 10 yi 5 1 2 4 3 8 7 6 9 10. Вычислим di: d1 = 1 – 5 = -4; d2 = 2 – 1 = 1; d3 = 3 – 2 = 1; d4 = 4 – 4 = 0; d5 = 5 – 3 = 2; d6 = 6 – 8 = -2; d7 = 7 – 7 = 0; d8 = 8 – 6 = 2; d9 = d10 = 0. Найдем Приступим к вычислению коэффициента корреляции Кендалла. Определим, сколько рангов, больших данного, располагается справа от каждого yi: R1 = 5; R2 = 8; R3 = 7; R4 = 5; R5 = 5; R6 = 2; R7 = 2; R8 = 2; R9 = 1; R10 = 0; R = 5 + 8 + 7 + 5 + 5 + 2 + 2 + 2 + 1 = 37; Заметим, что величины выборочных коэффициентов корреляции позволяют предполагать существование связи между результатами экзаменов. Для проверки этого предположения следует проверить гипотезу о значимости соответствующего выборочного коэффициента ранговой корреляции.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 436. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
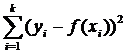 принимает минимальное значение.
принимает минимальное значение.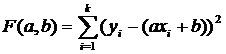 , то из условия
, то из условия  получаем:
получаем: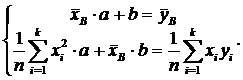 (7)
(7)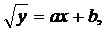 и система для определения a, b может быть получена по аналогии с предыдущим случаем с помощью замены yi на
и система для определения a, b может быть получена по аналогии с предыдущим случаем с помощью замены yi на 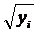 :
: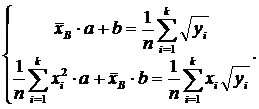 (8)
(8)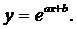 Логарифмируя, получаем: lny=ax + b, и система уравнений для a, b имеет вид:
Логарифмируя, получаем: lny=ax + b, и система уравнений для a, b имеет вид: (9)
(9) Тогда y2 = ax + b, и условия для а и b можно задать так:
Тогда y2 = ax + b, и условия для а и b можно задать так: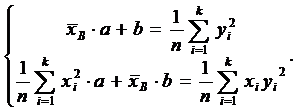 (10)
(10)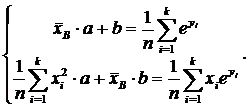 (11)
(11) = 3,1;
= 3,1; 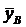 = 40,0;
= 40,0; 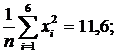
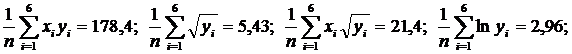
 Теперь можно решать линейные системы для а и b:
Теперь можно решать линейные системы для а и b: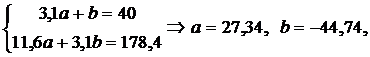 то есть линейная зависимость имеет вид: у = 27,34х – 44,74.
то есть линейная зависимость имеет вид: у = 27,34х – 44,74.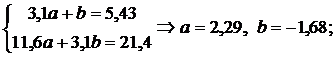 квадратичная функция:
квадратичная функция: 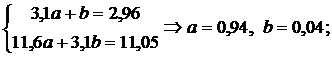 показательная функция:
показательная функция: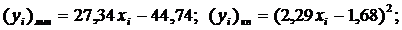
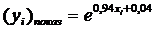 :
: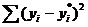
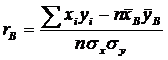 . (11)
. (11)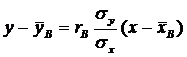 (12)
(12)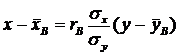 . (13)
. (13)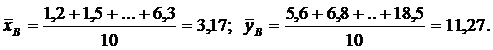
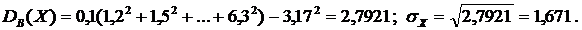
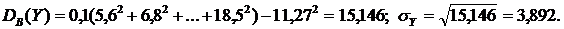 Для определения выборочного коэффициента корреляции вычислим предварительно
Для определения выборочного коэффициента корреляции вычислим предварительно  Тогда
Тогда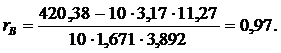 Выборочное уравнение прямой линии регрессии Y на Х имеет вид:
Выборочное уравнение прямой линии регрессии Y на Х имеет вид: 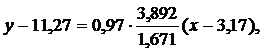 или
или 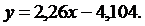
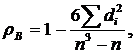 (14)
(14)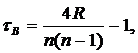 (15)
(15)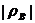 или
или 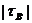 к 1, тем теснее возможная связь между признаками А и В.
к 1, тем теснее возможная связь между признаками А и В.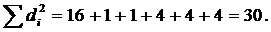 Тогда выборочный коэффициент ранговой корреляции Спирмена
Тогда выборочный коэффициент ранговой корреляции Спирмена