
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Точечные оценки параметров распределенияПо имеющейся выборке можно дать оценку математического ожидания и дисперсии генеральной совокупности. Оценкой математического ожидания служит выборочное среднее
то есть среднее арифметическое всех элементов выборки, а оценкой дисперсии – выборочная дисперсия
Заданная таким образом оценка математического ожидания является несмещенной, то есть математическое ожидание выборочного среднего равно оцениваемому параметру (математическому ожиданию исследуемой случайной величины). Выборочная дисперсия, напротив, смещенная оценка генеральной дисперсии, и
Соответственно число Пример 3. Найти выборочное среднее, исправленную выборочную дисперсию и исправленное среднее выборочное отклонение для выборок, заданных в примерах 1 и 2. Решение. 1)
2) В выборке из примера 2 будем считать вариантами середины частичных интервалов, то есть определим точечные оценки для выборки (Таблица 3): Таблица 3
Тогда
Интервальные оценки параметров распределения Точечная оценка при малом объеме выборки может существенно отличаться от оцениваемого параметра, поэтому важно знать, насколько истинное значение параметра может отклоняться от найденной точечной оценки. Интервал вида 
где а – оцениваемое математическое ожидание, хВ – выборочное среднее, п – объем выборки, t – такое значение аргумента функции Лапласа Ф (t), при котором При неизвестном среднем квадратическом отклонении доверительный интервал для математического ожидания при заданной надежности γ задается так:
Здесь s – исправленное выборочное среднее квадратическое отклонение, а Для оценки генерального среднего квадратического отклонения σ при заданной надежности γ можно построить доверительный интервал вида
где s – исправленное выборочное среднее квадратическое отклонение, а q = q (n, γ) – значение, определяемое из таблиц.
Пример 4. Дана выборка значений нормально распределенной случайной величины: 2, 3, 3, 4, 2, 5, 5, 5, 6, 3, 6, 3, 4, 4, 4, 6, 5, 7, 3, 5. Найти с доверительной вероятностью γ = 0,95 границы доверительных интервалов для математического ожидания и дисперсии. Решение. Объем выборки п = 20. Найдем
доверительный интервал для математического ожидания;
|
||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 382. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) . (2)
. (2)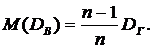 Поэтому вводится несмещенная оценка генеральной дисперсии – исправленная выборочная дисперсия
Поэтому вводится несмещенная оценка генеральной дисперсии – исправленная выборочная дисперсия (3)
(3) является несмещенной точечной оценкой среднего квадратического отклонения.
является несмещенной точечной оценкой среднего квадратического отклонения.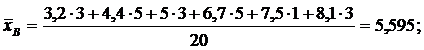
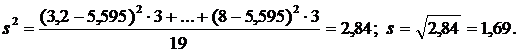


 где Ө - истинное значение оцениваемого параметра, а Ө* - его точечная оценка, называется доверительным интервалом, а вероятность
где Ө - истинное значение оцениваемого параметра, а Ө* - его точечная оценка, называется доверительным интервалом, а вероятность 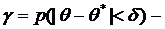 доверительной вероятностью или надежностью. Для построения доверительного интервала требуется знать закон распределения исследуемой случайной величины. Пусть эта величина распределена по нормальному закону. Если при этом известно ее среднее квадратическое отклонение σ, то доверительный интервал для математического ожидания имеет вид:
доверительной вероятностью или надежностью. Для построения доверительного интервала требуется знать закон распределения исследуемой случайной величины. Пусть эта величина распределена по нормальному закону. Если при этом известно ее среднее квадратическое отклонение σ, то доверительный интервал для математического ожидания имеет вид: (4)
(4)
 (5)
(5)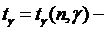 критическая точка распределения Стьюдента, значение которой можно найти из таблиц по известным п и γ.
критическая точка распределения Стьюдента, значение которой можно найти из таблиц по известным п и γ.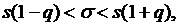 (6)
(6) = 4,25, s = 1,37. По таблицам 3 и 4 определим t (0,95; 20) = 2,093; q (0,95; 20) = 0,37. Тогда
= 4,25, s = 1,37. По таблицам 3 и 4 определим t (0,95; 20) = 2,093; q (0,95; 20) = 0,37. Тогда
 доверительный интервал для дисперсии.
доверительный интервал для дисперсии.