
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
II. Экспериментальный раздел работыСтр 1 из 14Следующая ⇒ Программирование На языке высокого уровня СИ
ЧАСТЬ II практикум
Рыбница, 2010 УДК 681.3.06 ББК 32.973.2-018 П 78
Программирование на языке высокого уровня СИ. Часть II: практикум/ Сост. О. В. Шестопал, О. В. Сташкова. – Тирасполь, 2010. – 83 с.
Практикум составлен в соответствии с учебной программой по дисциплинам «Программирование на языке высокого уровня» для студентов 1 курса специальности «Программное обеспечение вычислительной техники и автоматизированных систем». Практикум (II часть) включает в себя 5 лабораторных работ по структурированным типам данных: массивы, строки, перечисляемый и диапазонный типы данных, структуры и объединения, файлы. Особое внимание уделено вопросам программирования рекурсивных алгоритмов. Каждая из лабораторных работ включает теоретический материал, экспериментальный и самостоятельный разделы. Порядок расположения материала соответствует последовательности его изучения. Основные цели предлагаемого практикума – придать курсу программирования научно-обоснованный базис, сформировать на его основе определенную культуру проектирования и разработки программ.
Рецензенты: В.Е. Лозовский, учитель высшей категории, директор МОУ «Рыбницкая средняя образовательная школа №6 с лицейскими классами» А.Б. Глазов, ст. преп. кафедры «ФМИ»
Рекомендовано Научно-методическим советом ПГУ им. Т.Г. Шевченко Протокол № _______от ____________ 2010 г.
© Составление О.В. Шестопал, О.В.Сташкова, 2010 г.
Содержание Работа 1.ПОЛЬЗОВАТЕЛЬСКИЕ ФУНКЦИИ В СИ.. 5  Работа 2.СТРУКТУРИРОВАННЫЙ ТИП ДАННЫХ МАССИВ.. 16 Работа 3. СИМВОЛЬНЫЙ И СТРОКОВЫЙ ТИПЫ ДАННЫХ.. 32 Работа 4.СТРУКТУРЫ.. 44 Работа 5. РАБОТА С ФАЙЛАМИ.. 54 СПИСОК ЛИТЕРАТУРЫ... 66
Работа 1. ПОЛЬЗОВАТЕЛЬСКИЕ ФУНКЦИИ В СИ
Цель работы: – изучить суть работы с подпрограммами; – изучить правила описания подпрограмм и обращения к подпрограммам; – изучить понятие и виды рекурсии; – научиться решать задачи с использованием подпрограмм; – научиться применять рекурсию для решения задач.
I. Теоретический раздел работы Функции Любая Си-программа составляется из "строительных блоков", именуемых функциями. Функция — это подпрограмма, которая содержит одну или несколько Си-инструкций и выполняет одну или несколько задач. Хороший стиль программирования на Cи предполагает, что каждая функция выполняет только одну задачу. Каждая функция имеет имя, которое используется для ее вызова. Своим функциям программист может давать любые имена за исключением имени main (), зарезервированного для функции, с которой начинается выполнение программы. В Cи ни одна функция не может быть встроена в другую: все функции рассматриваются как отдельные компоненты. (Безусловно, одна функция может вызывать другую.) Прототип объявляет функцию до ее первого использования. Общий формат Си-функций Общий формат Си-функций:
тип_возвращаемого_значения имя (список_параметров) { тело функции } Рассмотрим подробно все элементы, составляющие функцию. С помощью элемента тип_возвращаемого_значенияуказывается тип значения, возвращаемого функцией. Если функция не возвращает никакого значения, необходимо указать тип void. Если функция действительно возвращает значение, оно должно иметь тип, совместимый с указанным в определении функции. Каждая функция имеет имя. Оно, как нетрудно догадаться, задается элементом имя. После имени функции между круглых скобок указывается список параметров, который представляет собой последовательность пар (состоящих из типа данных и имени), разделенных запятыми. Если функция не имеет параметров, элемент список_параметров отсутствует, т.е. круглые скобки остаются пустыми. В фигурные скобки заключено тело функции. Тело функции составляют Си-инструкции, которые определяют действия функции. Функция завершается (и управление передается вызывающей процедуре) при достижении закрывающей фигурной скобки или инструкции return. Аргументы функций Функции можно передать одно или несколько значений. Значение, передаваемое функции, называется аргументом. Верхний предел числа принимаемых аргументов определяется конкретным компилятором. Согласно стандарту Cи он равен 256. Аргумент — это значение, передаваемое функции при вызове. Параметр — это определяемая функцией переменная, которая принимает передаваемый функции аргумент. При создании функции, которая принимает один или несколько аргументов, иногда необходимо объявить переменные, которые будут хранить значения аргументов. Эти переменные называются параметрами функции. Например, следующая функция выводит произведение двух целочисленных аргументов, передаваемых функции при ее вызове. void mul(int x, int у) { cout << x * у << " " ; } При каждом вызове функции mul() выполняется умножение значения, переданного параметру х, на значение, переданное параметру у. Однако помните, что х и у — это просто переменные, которые принимают значения, передаваемые при вызове функции. Если вы никогда не работали с языком программирования, в котором разрешены параметризованные функции, описанный процесс может показаться несколько странным. Однако волноваться не стоит: по мере рассмотрения других Си-программ принцип использования функций, их аргументов и параметров станет более понятным. Примечание.Термин аргумент относится к значению, которое используется при вызове функции. Переменная, которая принимает этот аргумент, называется параметром. Функции, которые принимают аргументы, называются параметризованными функциями. Если Си-функции имеют два или больше аргументов, то они разделяются запятыми - список аргументов. Функции, возвращающие значения. В Cи многие библиотечные функции возвращают значения. Например, уже знакомая функция abs () возвращает абсолютное значение своего аргумента. Функции, написанные программистом, также могут возвращать значения. В Cи для возврата значения используется инструкция return. Общий формат этой инструкции таков: return значение; Нетрудно догадаться, что здесь элемент значение представляет собой значение, возвращаемое функцией. В более ранних версиях СИ для типов значений, возвращаемых функциями, существовало соглашение, действующее по умолчанию. Если тип возвращаемого функцией значения не указан, предполагалось, что эта функция возвращает целочисленное значение. Несмотря на то, что большинство компиляторов поддерживают это правило ради, обратной совместимости, вы должны явно задавать тип значения, возвращаемого каждой функцией, которую пишете. При достижении инструкции return функция немедленно завершается, а весь остальной код игнорируется. Функция может содержать несколько инструкций return. Возврат из функции можно обеспечить с помощью инструкции return без указания возвращаемого значения, но такую ее форму допустимо применять только для функций, которые не возвращают никаких значений и объявлены с использованием ключевого слова void. Функция main () Функция main () — специальная, поскольку это первая функция, которая вызывается при выполнении программы. В отличие от некоторых других языков программирования, в которых выполнение всегда начинается "сверху", т.е. с первой строки кода, каждая С++-программа всегда начинается с вызова функции main () независимо от ее расположения в программе. (Все же обычно функцию main () размещают первой, чтобы ее было легко найти.) В программе может быть только одна функция main (). Если попытаться включить в программу несколько функций main (), она "не будет знать", с какой из них начать работу. В действительности большинство компиляторов легко обнаружат ошибку этого типа и сообщат о ней. Как упоминалось выше, поскольку функция main () встроена в язык СИ, она не требует прототипа.
Рекурсия. Если какую-либо группу операторов необходимо было многократно повторить, то нами использовались операторы цикла. Одна и та же последовательность действий, выполняемая на различных этапах обработки информации, оформлялась нами в виде самостоятельной программной единицы – процедуры или функции. Процедуры и функции позволяют не только сократить объем программы, улучшить ее структуру и наглядность а, следовательно, и понимание, но являются также эффективным средством проектирования программных продуктов. Подпрограммы, записанные однократно в описательной части, могут быть вызваны по имени, как в теле основной программы, так и в других подпрограммах. В языке С++ существует еще одна уникальная возможность вызова подпрограммой самой себя. Такие процедуры и функции называются рекурсивными. Различают прямую рекурсию, когда подпрограммы обращаются к своему имени в «недрах» себя, и косвенную, когда ссылка на нее идет через цепочку других процедур и функций. В данной работе мы познакомимся с некоторыми простейшими рекурсивными алгоритмами. С понятием рекурсия тесно связано понятие рекуррентное соотношение (оба слова имеют общий корень от латинского recurro – возвращаться, бежать назад). Запишем в общем виде рекуррентное соотношение порядка к:
f(n) = G (n, f (n - 1),f (n - 2), … f (n - k)), (1)
где G – некоторая функция к + 1 аргумента. Если известны начальные значения f(1), f(2), …f(k), то выражение (1) позволяет однозначно определить f(n). Выбрав другие начальные условия, получим тем же способом другую функцию от n, удовлетворяющую (1). Каждая такая функция является решением данного рекуррентного соотношения. Как правило, программы, записанные в виде рекурсивных процедур и функций отличаются простотой и компактностью записи текста. Рекурсия – мощный инструмент в руках программиста. Однако им необходимо умело пользоваться, знать его сильные и слабые стороны. Принцип работы рекурсивных подпрограмм подобен работе стека. Прямой ход рекурсии – операция засылки информации в стек (операция Push): Обратный ход рекурсии – последовательное извлечение данных из стека (операция Pop): В прямом ходе, при очередном вызове подпрограммы-функции все ее локальные переменные, а также параметры, заносятся в специальную область памяти (сегмент стека), причем копии всех обращений временно сохраняются. Число копий, находящихся в памяти, т.е. число рекурсивных вызовов подпрограммы без возврата, называется глубиной рекурсии. В прямом ходе рекурсии это число возрастает. Следует помнить, что размеры стека не бесконечны (по умолчанию, объем стека равен 16 Кбайт), и существует реальная опасность его переполнения. Кроме того, в рекурсивном алгоритме обязательно должно быть условие, гарантирующее завершение цепочки обращений к функции. При обратном ходе оперативная память, занятая под локальные переменные и параметры функции освобождается, а полученный результат передается в точку возврата – оператор присваивания значений вычисляемой функции.
II. Экспериментальный раздел работы
Пример 1. Вычисление факториала. Факториал числа n! определяет количество способов размещения n предметов в некотором ряду. Так, при n=3 имеется три способа для размещения первого предмета. Если он уже зафиксирован, то существует два способа установки второго предмета и один для третьего. Таким образом, 3!=3*2*1=6. Приведем таблицу для нескольких первых значений факториала: 4!=24; 5!=120; 6!=720; 7!=5040; 8!=40320 … Характерной особенностью этой величины является ее экспоненциальное возрастание. При больших значениях n справедлива следующая оценка Стирлинга:
Некоторые важные свойства факториала можно найти в справочной литературе, а мы подробнее остановимся на рекурсивном алгоритме его вычисления. Запишем факториал в виде n! = n (n-1)! (3) В такой записи задача вычисления факториала сводится к ней самой же, путем изменения исходных данных, т.е. «новое» значение n! выражено через «старое» (n-1)!. Кроме того, условие 0! =1 позволяет завершить вычислительный процесс. Составим рекурсивную функцию:
double Factorial(int number) { if (number > 1) return number * Factorial(number - 1); return 1; }
Рис 1. Рекурсивные вызовы функции для выражения factorial(5). Пример 2. Алгоритм Евклида. Построим рекурсивные алгоритмы вычисления наибольшего общего делителя НОД (n,m) двух целых чисел n и m. Говорят, что два целых числа делятся (или n кратно m), если n=k*m, где k – целое число. Наибольший общий делитель – это максимальное значение числа k, которое делит и n и m. Например,
НОД (39, 15)=3, НОД (18, 12)=6.
Геометрическая трактовка НОД (n, m) – это набольшая общая мера двух соизмеримых отрезков, т.е. отрезков, каждый из которых в n и m-раз соответственно длиннее, чем некоторый выбранный отрезок - масштаб. Такая геометрическая иллюстрация НОД подсказывает простейший, буквально следующий определению, алгоритм его нахождения. Действительно, выберем из двух отрезков наименьший и проверим, не укладывается ли он целое число раз в другом. Если да, то цель достигнута. Если нет, то возьмем половину меньшего отрезка и проверим, не укладывается ли он целое число раз в другом. В случае неудачи перейдем к трети отрезка и т.д. Условие соизмеримости отрезков гарантирует успешное окончание этого процесса. Представим описанный алгоритм в виде подпрограммы-функции int Nod(int n,int m) { int i,k,rez; if(n>m) k=m; else k=n; for(i=1;i<=k;i++){ if((m%i==0)&&(n%i==0)) rez=i;} return rez; } Нетрудно заметить, что такой алгоритм неэффективен, поскольку предполагает выполнение многих лишних действий по перебору нужного варианта (при n>m необходимо выполнить m - действий). Существенно более выгодным является метод, предложенный Евклидом более 2300 лет назад. Рассмотрим две его трактовки в связи с возможностью их рекурсивной реализации. Алгоритм Евклида строится, опираясь на свойства наибольшего общего делителя. Сформулируем их:
1. НОД (n, m) = НОД (-n, m) = НОД (n,-m); 2. НОД (n, m) = НОД (n - m, m) = НОД (n, m - n); 3. НОД (n, 0) = n, при n 4. НОД (n, m) = НОД ( m, n mod m);
В записи этих свойств уже заложена рекурсивная трактовка. Рассмотрим сначала более подробно свойства 3 и 4. Пусть a0 = n, а1= m. Основываясь на указанных свойствах можно сформировать последовательность остатков от деления а2, а3,…, используя рекуррентное соотношение
Продолжая этот процесс до тех пор, пока an+1 =0, получим
НОД (a0,a1) = НОД (a1,a2) = …= НОД (an,0) = an (5) Данную последовательность можно записать в более привычном виде:
где qk - целые числа. Например, НОД (39,15) = НОД (15,9) = НОД (9,6) = НОД (6,3) = НОД (3,0) = 3
Действительно, разложив на множители эти числа 39 = 3*13 и 15 = 3*5, получим НОД (39,15)= 3. Поскольку нет необходимости запоминать промежуточные результаты и, следовательно, вводить массив целых чисел, запишем алгоритм Евклида так:
1. Ввод исходных данных: n,m; 2. Повторить r = n mod m; n = m; m = r пока r = 0; 3. Вывод результата: НОД (n,m) = n.
Составим подпрограмму-функцию: int Nod_2(int n,int m) { int r=n%m; if(r==0) return m; else return Nod_2 (m,r); } Составьте подпрограммы вычисления НОД на основе свойств 1 и 2. Настоятельно рекомендуется поэкспериментировать с приведенными функциями, сравнить их по количеству действий, эффективности действий, наглядности и т.д.
Пример 3. Решение нелинейных уравнений. Рассмотрим задачу нахождения корней нелинейного уравнения
f(x)=0 (6) Алгоритм нахождения корней приближенными методами можно разбить на два этапа. На первом – изучается расположение корней и проводится их разделение. Находится область [a,b], в которой существует корень уравнения или начальное приближение к корню x0. Простейший способ выделения корней – табуляция функции и анализ ее графика. Существование на найденном отрезке [a,b], по крайней мере, одного корня уравнения (6) следует из условия, что знаки функций на концах отрезка различны:
f(a) ∙ f(b) < 0 (7) При этом подразумевается, что функция f(x) непрерывна и монотонна на данном отрезке На втором этапе решения, используя полученное начальное приближение, стоится итерационный процесс, позволяющий уточнять значение корня с некоторой, наперед заданной точностью
Рассмотрим простейший метод уточнения значения корня с заданной точностью 1. Задания значений величин 2. Последовательно выбранный отрезок делится пополам и осуществляется выбор того из двух отрезков, на котором функция меняет знак. 3. Вычисление заканчивается, если выполнено условие (8), иначе возврат к шагу 2. Приведем рекурсивный вариант программы-функции, реализующей описанный метод:
double X_Dich(double a, double b, double eps){ double x; if (f(a)*f(b)> 0.0) {cout<<”error”};exit;} else { x=0.5*(a+b); if (abs(f(x)) > eps) { if (f(a)*f(x) <0.0) Return X_Dich(a,x,eps); Else Return X_Dich(x,b,eps); Return x; } } Изучите приведенный алгоритм, проведите отладку программы и сделайте её тестирование. В качестве теста используйте любое уравнение с известным решением. В частности, можно рекомендовать уравнение Валлиса Полезно в своей библиотеке иметь не только подпрограммы-функции, но и процедуры, составленные на основе приведенных алгоритмов. Напишите их, выполните отладку и тестирование. Составьте подпрограммы с использованием рекурсии и без нее. Выбор очередной точки в середине отрезка не является единственным вариантом. Можно в качестве такой точки выбрать случайное число, заменив оператор x:=0.5*(a+b) на x:=a+(b-a)*random, предварительно инициализируя датчик случайных чисел Randomize. Проведите соответствующие расчеты и сравните требуемое число итераций для достижения заданной точности. Более совершенный метод выбора точки деления отрезка [a,b] – метод хорд, в котором в качестве x выбирается точка пересечения с осью абсцисс прямой y=Ax+B (хорды), проведенной через концы интервала u=f(a) и v=f(b).
Сделайте корректировку программы и проведите вычислительный эксперимент, сравнивая число итераций, требуемых для достижения заданной точности. Определите количество итераций разных методов, требуемых для достижения точности
Детальнее проанализировав этот алгоритм, нетрудно заметить, что выполняются лишние действия. Действительно, когда проводится повторный расчет с уменьшенным вдвое шагом, происходит повторное вычисление значений функции в некоторых из узлов. Проведите экспериментальные расчеты и проанализируйте их.
Пример 5. Рассмотрим рекуррентную числовую последовательность Фибоначчи, играющую важную роль в математике:
f(0) = 0; f (1) = 1 f (n) = f (n-1) + f (n-2), (12)
Запишем несколько первых значений последовательности чисел Фибоначчи: f(2)=1; f(3)=2; f(4)=3; f(5)=5; f(6)=8; f(7)=13;….. Простейшее рекуррентное соотношение второго порядка (12), в котором каждое следующее значение вычисляется по двум предыдущим, может быть естественным образом реализовано в виде рекурсивной функции:
int Fib(int n){ if (n= = Ø) return Ø; if (n = = 1) return 1; else return Fib(n – 2) + Fib(n-1) } Приведем не рекурсивный вариант решения данной задачи:
int Fib(int n){ int i,j,k,m; m=Ø; k=1; for(i=2; i<=n; i++){ j=k; k+=m; m=j; end; return k; } Сравнение этих подпрограмм показывает, что рекурсивный вариант организован не лучшим образом, он менее экономичен по числу обращений к функции. Это и понятно, вычисление слагаемого f(n) требует ссылки на f(n-1) и f(n-2). А вычисление слагаемого f(n-1), в свою очередь, на f(n-2) и f(n-3), т.е. происходит два независимых вычисления f(n-2). Это можно проиллюстрировать в виде следующего дерева графа для n = 4:
3 2
2 1
Из девяти вызовов функции f(n) - четыре сделаны повторно. Это неэффективно. Приведем аналитическое решение рекуррентного соотношения (6):
Нетрудно показать, что вычисление по рекурсивному алгоритму требует Данный пример показывает неудачное применение рекурсии и указывает на необходимость тщательного анализа используемых алгоритмов. Красиво не всегда означает эффективно. Кстати и циклические вычисления не застрахованы от плохой реализации, где могут, например, повторяться уже проделанные операции. Но, как правило, итерационные алгоритмы более прозрачны с точки зрения их анализа, в отличие от рекурсивных, где заметить дефекты бывает значительно труднее. Несмотря на сказанное, рекурсия это мощный инструментарий, позволяющий легко реализовывать многие сложные алгоритмы. Но об этом еще разговор впереди, а сейчас нужно освоить простейшие навыки составления рекурсивных подпрограмм.
III. Задания для самостоятельной работы
A. 1. Вычислить числа Фибоначчи второго порядка: u0 =1; u1 =2; u2 =3 un = un-1 + un-2 + un-3 , при n=3, 4,… 2. Написать рекурсивную функцию для вычисления значения так называемой функции Аккермана для неотрицательных чисел n и m. Функция Аккермана определяется следующим образом: 3. Вычислить рекурсивно функцию:
n –10, если n>100 F(n)= F(F(n+4)), если n<100
4. Вычислить рекурсивно функцию :
S(n) S(n/2), если n=2k S((3n+1)/2), если n=2k+1
5. Написать рекурсивную и нерекурсивную функции вычисления биномиальных коэффициентов:
C(n,0) = C(n,n) = 1 C(m,n) = C(m,n-1) + C(m-1,n-1) при 0 < m < n 6. Написать рекурсивную и нерекурсивную функции для разностного уравнения А(0) = 1 A(n) = A(ndiv2)+A(ndiv3) 7. Написать рекурсивную функцию: а) вычисления суммы цифр натурального числа; б) вычисления количества цифр натурального числа. 8. Даны первый член и разность арифметической прогрессии. Написать рекурсивную функцию для нахождения: а) n-го члена прогрессии; б) суммы n первых членов прогрессии. 9. Даны первый член и знаменатель геометрической прогрессии. Написать рекурсивную функцию: а) нахождения ее n-го члена; б) нахождения суммы n первых членов прогрессии. B. 1. Вычислить рекурсивно полином Лежандра порядке n:
P0(x) = 1; P1(x) = x; Pn(x)=((2n-1)Pn-1(x) - (n-1)Pn-2(x)/n
2. Написать рекурсивную и не рекурсивную функции вычисления полинома Чебышева первого ряда:
T0(x)=1; T1(x)=x Tn(x)=2xTn-1(x) – Tn-2(x) Сравнить число операций. 3. Написать рекурсивную и не рекурсивную функции вычисления полинома:
H0(x)=1; H1(x)=x Hn(x)=xHn-1(x) –(n-2)Hn-2(x) Сравнить число операций. 4. Написать рекурсивную и не рекурсивную функции вычисления полинома:
G0(x)=1; G1(x)=x-1 Gn(x)=(x-2n+1)Gn-1(x) –(n-1)2Gn-2(x) Сравнить число операций. 5. Написать рекурсивную и не рекурсивную функции вычисления полинома:
L0(x)=1; L1(x)=x Сравнить число операций. 6. Написать рекурсивную и не рекурсивную функции вычисления полинома Эрмита
H0(x)=1; H1(x)=2x Hn(x)=2xHn(x) – 2nHn-1(x) 7. Написать рекурсивную и не рекурсивную функции вычисления полинома Лагерра: L0(x)=1; L1(x)=1-x. 8. Вычислить рекурсивно и нерекурсивно: где k!! = 1*3*5*…k, если k – нечетно k!! = 2*4*6*…k, если k - четно 9. Вычислить, используя рекурсию и без нее:
а) б) в) г) д) е)
C. 1. Используя команды write(x) лишь при х=0,1,…9 написать рекурсивную процедуру вывода на экран десятичной записи натурального числа n. 2. Используя команды write(x) лишь при х=0,1 написать рекурсивную процедуру вывода на экран двоичной записи натурального числа n. 3. Используя команды write(x) лишь при х=0,1,…9 написать рекурсивную процедуру вывода на экран восьмеричной записи натурального числа n. 4.Написать рекурсивную и нерекурсивную функции возведения вещественного числа х в натуральную степень n. 5. Цифровой корень натурального числа находится через сумму цифр этого числа до тех пор, пока эта сумма не станет цифрой. Написать рекурсивную функцию нахождения цифрового корня натурального числа. 6. Написать рекурсивную процедуру перевода числа из десятичной системы в N –ю (2<= N <= 16). 7. Составить рекурсивную функцию нахождения суммы первых n членов арифметической и геометрической прогрессий. 8. Составить рекурсивную процедуру нахождения максимального элемента в массиве. 9. Написать рекурсивный алгоритм головоломки «ханойская башня». 10. Написать рекурсивный алгоритм перевода из двоичной системы счисления в десятичную ( из восьмеричной и шестнадцатеричной в десятичную). 11. Написать рекурсивный алгоритм представления натурального числа в римском исчислении. 12. Написать рекурсивную процедуру для вывода на экран цифр натурального числа в обратном порядке. 13. Написать рекурсивную процедуру перевода натурального числа из десятичной системы счисления в N-ичную. Значение N в основной программе вводится с клавиатуры (2 14. Написать рекурсивную функцию, определяющую, является ли заданное натуральное число простым (простым называется натуральное число, большее 1, не имеющее других делителей, кроме единицы и самого себя). |
||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 303. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . (2)
. (2)
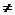 0;
0; (4)
(4)
 .
. (8)
(8) и вычисления значений функции u=f(a), v:=f(b).
и вычисления значений функции u=f(a), v:=f(b).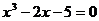 , имеющего один вещественный корень 2.09455.
, имеющего один вещественный корень 2.09455.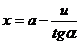 , где
, где  . (9)
. (9)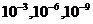 .
.



 4
4 1 0
1 0 (13)
(13)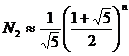 обращений к функции, в отличие от N1 = (n – 2) обращений во второй программе, использующей цикл. Зависимость N1 от n - линейная, а N2 от n - показательная с основанием
обращений к функции, в отличие от N1 = (n – 2) обращений во второй программе, использующей цикл. Зависимость N1 от n - линейная, а N2 от n - показательная с основанием  , т.е.
, т.е.  .
.

 1, если n=1
1, если n=1
 , n=1,2,
, n=1,2,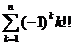 ,
, ;
; ;
;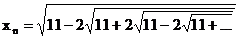 ;
; ;
; ;
;
 N
N