
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение критической нагрузки на грунт.
Теоретическая часть: Механические явления, возникающие в грунтах при возрастании на них местной нагрузки при давлениях на грунт больше структурной прочности можно разделить на два вида: 1) начало возникновения в грунте зон сдвига и окончание фазы уплотнения, когда под краем нагрузки между касательными и нормальными напряжениями возникают соотношения, приводящие грунт в предельное состояние, нагрузка при которой происходит это явление называется начальной. 2) под нагруженной поверхностью формируются сплошные области предельного равновесия, грунт приходит в неустойчивое состояние полностью исчерпав свою несущую способность, нагрузка при которой происходит это явление называется критической. Определение начальной критической нагрузки. Рассмотрим действие равномерно распределенной нагрузки p ( рис.3.1)на полосе шириной b при наличии боковой пригрузки q=γh ( где γ- плотность грунта , h- глубина залегания нагруженной поверхности).
 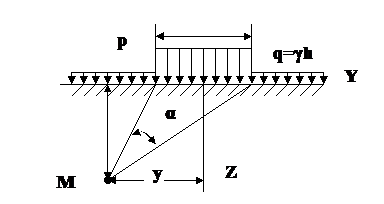
Рисунок 3.1.- Схема действия полосообразной нагрузки. Задача будет заключаться в определении такой нагрузки при которой зоны сдвига только зарождаются под нагруженной поверхностью. Так как при полосообразной нагрузке касательные напряжения будут наибольшими у краев нагрузки то в этих местах зарождаются зоны предельного равновесия. Принимая допущения о гидростатическом распределении давлений от собственного веса грунта , а также условия предельного равновесия для произвольной точки М определяют глубину z , характеризуемую углом видимости α и главными напряжениями:
 где c-сцепление грунта φ- угол внутреннего трения грунта. Принимая величину z как ординату области предельного равновесия и определив zmax=0 из равенства
Определение предельной нагрузки для сыпучих и связных грунтов. Предельная нагрузка, соответствующая полному исчерпанию несущей способности грунта и сплошному развитию зон предельного равновесия достигается для оснований фундаментов при окончании формирования жесткого ядра, деформирующего основание и распирающего грунт в стороны. Решение дифференциальных уравнений равновесия совместно с условиями предельного равновесия позволяет найти математически точные очертания поверхностей скольжения, используя которые, можно достаточно строго оценить значение предельной нагрузки на грунт, соответствующее максимальной несущей способности основания. Для невесомого грунта , нагруженного полосообразной нагрузкой определяется выражением:
Рисунок 3.2.-Сеть линий скольжения в грунте при полосообразной нагрузке и боковой пригрузке без учета собственного веса грунта. Для рассматриваемого случая ( рис. 3.2) получено следующее точное очертание линий скольжения: в треугольнике Ocd- два семейства параллельных прямых, наклоненных к горизонтали под углом При действии наклонной нагрузки с боковой пригрузкой на грунт, обладающей трением и сцеплением (рис.3.3) , вертикальная составляющая определяется выражением:
где- Nγ, Nq, Nc-коэффициенты несущей способности грунта, определяемые путем вычисления по построенной сетке линий скольжения как функции угла внутреннего трения и наклона нагрузки(таблица 3.1).
Рисунок 3.3.- Схема действия наклонной нагрузки на грунт.
Таблица 3.1. Значения коэффициентов несущей способности для случая действия наклонной полосообразной нагрузки.
Горизонтальная составляющая предельного давления на грунт определяется:
Если фундамент имеет конечную ширину b то при условии одностороннего выпирания для определения предельной несущей способности определяется: а) для края наклонной нагрузки (y=0)
б) для ординаты соответствующей ширине фундамента, при условии отсутствия выпирания в противоположную сторону
Тогда средняя величина вертикальной составляющей предельного давления на грунт :
Для оснований массивных фундаментов предельную нагрузку следует определять с учетом жесткого ядра ограниченных смещений, формирующегося под подошвой жестких фундаментов. В случае плоской задачи угол наклона жесткого ядра к подошве фундамента принимают δ=π/4 и определяют предельные давления:
где Nγп, Nqп, Ncп- коэффициенты несущей способности грунта для плоской задачи (таблица 4.2) b1-полуширина полосообразной нагрузки.
Таблица 4.2.- Значения коэффициентов несущей способности с учетом собственного веса грунта и уплотненного ядра для случая плоской задачи.
Задание: Определить значение начальной критической ,предельной нагрузки на грунт, а также предельной нагрузки с учетом возникновения под массивным ленточным фундаментом жесткого ядра , имеющим глубину заложения h и ширину подошвы b , если дано: угол внутреннего трения грунта φ, сцепление с и удельный вес γ.
Таблица 4.3.- Исходные данные.
Практическая работа №4.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 408. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (3.1)
(3.1) ,получаем величину начального критического давления:
,получаем величину начального критического давления: (3.2)
(3.2)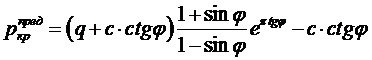 (3.3)
(3.3)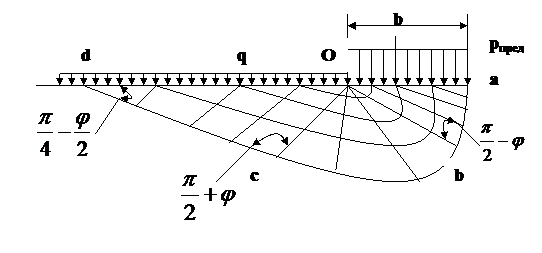
 ; в пределах угла сОb- пучок прямых , выходящих из точки О, и сопряженных с ними логарифмических спиралей; в треугольнике Оab( под подошвой нагрузки)- два семейства параллельных прямых, наклоненных под углом
; в пределах угла сОb- пучок прямых , выходящих из точки О, и сопряженных с ними логарифмических спиралей; в треугольнике Оab( под подошвой нагрузки)- два семейства параллельных прямых, наклоненных под углом  к горизонтали. Описанная сетка линий скольжения с заменой треугольника Oab очертанием жесткого ядра используется для приближенного определения предельной нагрузки на весомый грунт под жесткими фундаментами.
к горизонтали. Описанная сетка линий скольжения с заменой треугольника Oab очертанием жесткого ядра используется для приближенного определения предельной нагрузки на весомый грунт под жесткими фундаментами. (3.4)
(3.4)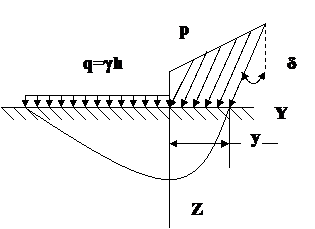
 (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) (3.8)
(3.8) (3.9)
(3.9)