Определение напряжений в грунтовом полупространстве от сосредоточенной силы для пространственной задачи.

Высшего образования

Рязанский государственный агротехнологический университет имени П.А. Костычева

Автодорожный факультет

Кафедра «Строительство инженерных сооружений и механика»

Механика грунта

Методические указания для выполнения практических работ

Для студентов направления

Строительство

Рязань 2015г.

Рассмотрена на заседании кафедры «Строительство инженерных сооружений и механика»

                                                   Протокол № ___________

                                                                «___»___________________2015  г

Заведующий кафедрой ,

д.т.н., профессор                                                                           Борычев С.Н.

Рецензент :

 к.т.н., доцент                                                           Тришкин И.Б.

Утверждено методической комиссией

 автодорожного факультета

                                                   Протокол № ___________

                                                                «___»___________________2015 г

Председатель учебно-методической комиссии

автодорожного факультета                                      Успенский И.А.

Рязань: ФГБОУ ВПО РГАТУ им. П.А.Костычева , 2013.-56с.

В методических указаниях представлены теоретические вопросы по проведению практических работ по основным разделам курса механики грунтов, с рекомендуемыми заданиями для самостоятельной работы.

СОДЕРЖАНИЕ

Введение ----------------------------------------------------------- -

1.Практическая работа №1. - ---------------------------------------

2. Практическая работа №2. - ---------------------------------------

3. Практическая работа №3. - ---------------------------------------

4. Практическая работа №4. - ---------------------------------------

5. Практическая работа №5. - ---------------------------------------

6. Практическая работа №6. - ---------------------------------------

7. Практическая работа №7. - ---------------------------------------

8. Приложения ----------------------------------------------------------

9.Литература -------------------------------------------------------------

Введение

Механика грунта есть теория естественных грунтовых оснований. Роль механики грунтов как инженерной науки огромна, и ее можно сравнить лишь с ролью дисциплины «Сопротивление материалов». Без знания основ механики грунтов не представляется возможным правильно запроектировать современные промышленные сооружения, жилые здания( особенно повышенной этажности), мелиоративные и дорожные, земляные и гидротехнические сооружения.

Применение механики грунтов позволяет особенно полно использовать несущую способность грунтов, достаточно точно учесть деформации грунтовых оснований под действием нагрузки от сооружений, что обуславливает принятие не только наиболее безопасных, но и наиболее экономичных решений.

Целью дисциплины является обеспечение базы инженерной подготовки: по обоснованию и принятию оптимальных решений по устройству оснований и фундаментов строительных транспортных сооружений в различных инженерно-геологических условиях, а также умения оценить их работоспособность, необходимых для изучения последующих дисциплин.

Задачами изучения дисциплины является умение и выработка знаний о современных подходах к расчету напряженного состояния и деформаций оснований, оценки устойчивости грунтовых массивов и давления грунта на транспортные сооружения сложных систем, освоение современных методов расчета, включая компьютерные технологии.

Требования к уровню освоения содержания дисциплины

В результате, изучения дисциплины студент должен:

Знать:

  - физические и механические свойства грунтов

-основы теории напряженного и деформированного состояния основания

- расчет оснований по деформациям, несущей способности и устойчивости

Уметь:

- определять физико-механические свойства грунтов

- производить расчеты оснований по деформациям, несущей способности и устойчивости

- оценивать устойчивость склонов, откосов и подпорных массивных стенок

В данных методических указаниях рассмотрены теоретические вопросы по основным разделам курса :распределение напряжений в грунтовом массиве; расчет оснований по деформациям; расчет оснований по несущей способности; расчет оснований по устойчивости по которым составлены задания для самостоятельной работы студентов.

Данный материал может быть использован студентами направления «Строительство» для изучения последующих специальных дисциплин, а также для курсового и дипломного проектирования.

Практическая работа №1.

Определение напряжений в грунтовом полупространстве от сосредоточенной силы для пространственной задачи.

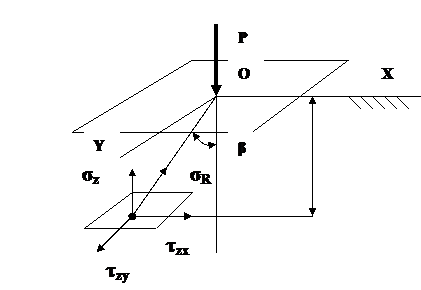
Теоретические сведения.

При определении напряжений в грунтовом полупространстве от сосредоточенной силы для пространственной задачи лежит положение о том, что в произвольной точке М грунтового полупространства появляется радиальное напряжение σ_R величина которого пропорциональна cos β и обратно пропорциональна квадрату расстояния R² от точки приложения сосредоточенной силы P ( рис.1.1.)

Рис. 1.1. Распределение напряжений при действии сосредоточенной силы в случае пространственной задачи.

Из рисунка 1.1. и с учетом коэффициента А, определяемого из условия равновесия получаем :

                           (1.1)

где                                           (1.2)

Проецируя далее σ_R из точки М(z,y,x) сначала на площадку , параллельную ограничивающей полупространство плоскости XOY, а затем на три направления , параллельные осям OZ, OX и OY , получим соответствующие величины составляющих напряжений (рис.1.2.):

                                  (1.3)

                                (1.4)

                                     (1.5)

Рис.1.2. Радиальное напряжение в линейно деформируемом полупространстве от сосредоточенной силы.

Для других площадок параллельных плоскостям XOZ и YOZ, а также в случае неоднородного грунтового основания все компоненты напряжений будут зависеть от коэффициента Пуассона ν. Тогда дополнительно имеем:

         (1.6)

          (1.7)

           (1.8)

Так как положение точки М полностью определяется ее глубиной z и расстоянием от оси OZ, поэтому формулу (1.3) представляют в виде:

                                                                                               (1.9)

где                                                                     (1.10)

Если к поверхности полупространства приложено несколько сосредоточенных сил, то напряжение σ_Z в расчетной точке М, расположенной на глубине z, определяется как сумма напряжений от действия каждой силы в отдельности:

                                                     (1.11)

где n- количество сосредоточенных сил.

 На практике давление на грунтовое основание от веса сооружения реализуется обычно не в точке, а через площадку, которая имеет определенное очертание в зависимости от вида инженерного сооружения. Поэтому в расчетах принимают прямоугольную площадку, длина которой не должна более чем в три раза принимать ее ширину. Возникающие в грунтовом основании напряжения находят с помощью специальных расчетных графиков(приложения рис П.1.,П.2.,П.3.) или таблиц по следующим формулам:

                                                                   (1.12)

где σ_z - вертикальные, σ_x σ_y- горизонтальные нормальные напряжения

ν_x μ_z ε_y – переходные коэффициенты, определяемые по графикам.

 P₀- интенсивность равномерно распределенной нагрузки, приложенной в пределах прямоугольной площадки шириной 2b и длиной 2a.

Напряжение в любой точке основания с любыми произвольными координатами может быть найдено как сумма угловых напряжений для прямоугольников, сходящихся в одной в данной точке и имеющих в ней общий угол ( метод угловых точек).

Для площадок под центром загруженного прямоугольника максимальное сжимающее напряжение определяется:

                                                           (1.13)

где К_с- табличный коэффициент определяемый по таблице 1.1

Таблица 1.1.- Значения коэффициента К_с для непосредственного определения максимальных сжимающих напряжений под центром загруженного прямоугольника.

Задание №1.

На поверхности грунтового массива приложена сосредоточенная сила Р. Определить вертикальное напряжение в точке М, возникающее только от действия силы Р без учета собственной силы тяжести грунта. Точка М расположена на глубине z от поверхности и на расстоянии r в стороне от вертикальной линии действия силы.

Таблица 1.2- Исходные данные.

Задание №2. Определить величину максимального сжимающего , вертикального и горизонтальных напряжений в точке М для условий объемной задачи под углом площадки размером a×b на глубине z от поверхности при удельной нагрузке Р₀=0,5 МПа. (схема а рис 1.3),    Р₀=0,8 МПа (схема б,рис 1.3).

Таблица 1.3- Исходные данные.

                       схема а                                                        схема б

Рисунок 1.3. Схема разбивки прямоугольной площадки загрузки.

Практическая работа №2.