
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Фукция распределения случайных величинДля описания закона распределения случайной величины Х возможен и другой подход: рассматривать не вероятности событий Функцией распределения случайной величины Х называется функция Функцию F(x) иногда называют интегральной функцией распределения или интегральным законом распределения. Геометрически функция распределения интерпретируется как вероятность того, что случайная точка Х попадет левее заданной точки х (рис. 6).
Рис. 6 Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равна вероятностям этих значений. Сумма всех скачков функции Общие свойства функции распределения 1. 2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси. 3. На минус бесконечности функция распределения равна 0, на плюс бесконечности равна 1, т.е. 4. Вероятность попадания случайной величины в интервал
Теоретические вопросы 1. Какая величина называется дискретной? Приведите примеры. 2. Чем можно задать дискретную случайную величину? 3. Какие числовые характеристики случайной величины вы знаете?  4. По каким формулам вычисляются математическое ожидание, дисперсия, среднее квадратическое отклонение, начальные и центральные теоретические моменты? 5. Что называется функцией распределения дискретной случайной величины? 6. Назовите свойства функции распределения?
ЗАНЯТИЕ 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Сведения из теории Случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек. Непрерывную случайную величину можно задать с помощью функции распределения вероятностей. Функцией распределения непрерывной случайной величины называется непрерывно дифференцируемая функция действительной переменной х, определяемая равенством Основные свойства функции распределения 1. 2. Функция распределения – неубывающая функция: если 3. Если все возможные значения случайной величины Х принадлежат интервалу (a;b) , то 4. Функция 5. Если все возможные значения случайной величины Х принадлежат бесконечному интервалу Введем понятие плотности вероятности непрерывной случайной величины (другое задание непрерывной случайной величины). Плотностью вероятности (плоскостью распределения или просто плотностью) Про случайную величину Х говорят, что она имеет распределение с плотностью Плотность вероятности иногда называют дифференциальной функцией или дифференциальным законом распределения. Свойства плотности вероятности 1. 2. Вероятность попадания непрерывной случайной величины в интервал 3. Функция распределения непрерывной случайной величины X может быть выражена через плотность вероятности по формуле:
4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины Х равен 1, т.е.
Геометрические свойства 1 и 4 плотности вероятности означают, что ее график – кривая распределения лежит не ниже оси ОХ, и полная площадь фигуры, ограниченной кривой распределения с осью ОХ, равна 1.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 249. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
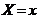 для разных х, а вероятности события
для разных х, а вероятности события  , где х – текущая переменная. Вероятность
, где х – текущая переменная. Вероятность 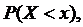 очевидно, зависит от х, т.е. является некоторой функцией от х.
очевидно, зависит от х, т.е. является некоторой функцией от х.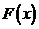 , выражающая для каждого х вероятность того, что случайная величина Х примет значение, строго меньшее х, т.е.
, выражающая для каждого х вероятность того, что случайная величина Х примет значение, строго меньшее х, т.е. . (40)
. (40)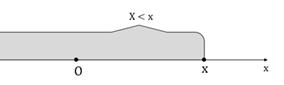
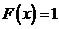 .
. .
.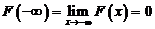 и
и  .
. равна приращению ее функции распределения на этом интервале, т.е.
равна приращению ее функции распределения на этом интервале, т.е. 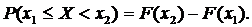
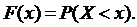
 .
. при
при  ,
,  .
. непрерывна слева, т.е.
непрерывна слева, т.е. 
 , то
, то 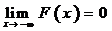 и
и  .
.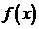 непрерывной случайной величины Х называется производная ее функции распределения, т.е.
непрерывной случайной величины Х называется производная ее функции распределения, т.е. . (41)
. (41) 
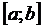 равна определенному интегралу от ее плотности вероятности в пределах от a до b, т.е.
равна определенному интегралу от ее плотности вероятности в пределах от a до b, т.е. . (42)
. (42) . (43)
. (43) . (44)
. (44)