Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙСтр 1 из 5Следующая ⇒ ЗАНЯТИЕ 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ Сведения из теории Теория вероятностей – раздел математики, изучающей закономерности случайных явлений, наблюдаемых при массовых повторениях испытаний. Основным понятием теории вероятностей является понятие события. Событием (или «случайным событием») называется всякий факт, который в результате опыта (испытания) может произойти или не произойти. События обозначаются прописными (заглавными) буквами латинского алфавита: А, В, С,…
Полной группой событий называется несколько событий таких, что в результате опыта одно из них непременно должно произойти. События называются несовместными, если наступление одного из них исключает наступление любого другого. В противном случае события называются совместными. Например, получение студентом на экзамене по одной дисциплине оценок «отлично», «хорошо» и «удовлетворительно» – события несовместные, а получение тех же оценок на экзаменах по трем дисциплинам – события совместные. События называются равновозможными, если условия их появления одинаковы и нет оснований считать какое-либо из них более возможным, чем любое другое. Например, появление герба или решки при подбрасывании монеты.  Два события называются противоположными, если в одном эксперименте одно из них обязательно появится и его появление исключает появление другого. Несколько событий называются элементарными, если они образуют полную группу событий и равновозможны (т.е. единственно возможны, несовместны и равновозможны). Совокупность всех элементарных событий будем называть пространством элементарных событий, а сами элементарные события – точками этого пространства. Все события, связанные с данным (идеализированным) опытом, могут быт описаны как совокупности элементарных событий. Замечание 1.1Если одно из двух противоположных событий обозначено A, то другое принято обозначать Ключевым понятием в теории вероятностей является понятие вероятности случайного события. Качественное определение. Численная мера степени объективной возможности наступления события называется вероятностью события. Определим теперь количественное определение. Введем предварительно следующие понятия: 1. Если несколько событий: а) образуют полную группу; б) несовместны; в) разновозможны, то они называются исходами («шансами»). 2. Исход называется благоприятным событию, если появление этого исхода влечет за собой появление события. Согласно классическому определению вероятность события A равна отношению числа случаев, благоприятствующих ему, к общему числу случаев, т.е. где P(A) – вероятность события A; m – число случаев, благоприятствующих событию A; n – общее число случаев (исходов). Свойства вероятности событий 1. Вероятность любого события заключена между 0 и 1, т.е. 2. Вероятность достоверного события равна единице. 3. Вероятность невозможного события равна нулю. Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно не применимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности, т.е. нахождение вероятности попадания точки в область (отрезок, часть плоскости, часть объема). Например, пусть плоская фигура g составляет часть плоской фигуры G (рис. 1). На фигуру G наудачу бросается точка. Это означает, что все точки области G «равноправны» в отношении показания туда брошенной случайной точки. Полагая, что P(A) – попадания брошенной точки на фигуру g – пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g, найдем
Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области, т.е.
Рис. 1
Осуществлять подсчет числа возможных исходов и числа благоприятных исходов в разных конкретных случаях помогают методы комбинаторики.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ Сведения из теории Комбинаторика – область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству. Общие правила комбинаторики Правило суммы. Если некоторый объект А можно выбрать из совокупности объектов m способами, а объект B можно выбрать k способами (не такими, как A), то объект «либо A, либо B» можно выбрать (m+k) способами. Правило произведения. Если объект А можно выбрать из совокупности объектов m способами, а после каждого такого выбора другой объект B можно выбрать (независимо от выбора объекта A) k способами, то пары объектов A и B можно выбрать (mk) способами. На практике часто приходится составлять выборки, к которым относятся: перестановки, размещения, сочетания. Перестановки Различные упорядоченные множества, которые отличаются лишь порядком элементов, т.е. могут быть получены из того же самого множества, называются перестановками где Например, А и В можно расположить одну за другой двумя способами А, В и В, А – две перестановки. Размещения Размещением из n элементов по m называются выборки, которые, имея по m элементов, выбранных из данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения
Например, A, B, C – размещены по два элемента Сочетания Сочетаниями из n элементов по m называются выборки, в каждую из которых входят m элементов, взятых из данных n элементов и которые отличаются только элементами (хотя бы одним, разница в порядке элементов не учитывается)
Например, A, B, C – сочетания по два элемента: Замечание 1.2Для решения практических задач часто оказывается полезной следующая формула обобщенной гипергеометрической вероятности: где Выборки с повторениями 1. Число размещений с повторениями – упорядоченная выборка с повторениями: Первый элемент размещения можно выбрать n способами, второй – n способами, третий – n способами, … 2. Сочетания с повторениями – неупорядоченная выборка с повторениями: 3. Число перестановок с повторениями из n элементов обозначается
Итоговая сводка формул приведена в следующей таблице:
Теоретические вопросы 1. Что изучает теория вероятностей? 2. Случайное событие, его виды (приведите примеры). 3. Какие события называются несовместными (приведите примеры). 4. Сформулируйте классическое определение вероятности и свойства вероятности. 5. Определение геометрической вероятности. 6. Основные правила комбинаторики. 7. Перестановки, размещения, сочетания (в том числе с повторениями).
ЗАНЯТИЕ 2. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Сведения из теории I. Теоремы сложения вероятностей Теорема сложения вероятностей несовместных событий.Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий
Следствие 1. Теорема справедлива и для n несовместных событий
Следствие 2. Сумма вероятностей противоположных событий равна единице Следствие 3. Сумма вероятностей событий, образующих полную группу, равна единице. Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления Следствие 1. Для трех событий
Следствие 2. В случае трех и большего числа событий для нахождения вероятности суммы S этих событий проще найти вероятность противоположного события II. Теоремы умножения вероятностей Два события А и В называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события А и В называются зависимыми. Пусть А и В – зависимые события. Условной вероятностью Теорема умножения (А и В – зависимые события). Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие уже наступило Замечание 2.1Применив формулу (17) к событию
т.к.
Теорема умножения (А и В – независимые события). Вероятность произведения двух независимых событий равна произведению вероятностей этих событий
III.Формула полной вероятности. Формула Байеса (или Бейеса) Следствием двух основных теорем теории вероятностей – теоремы сложения и теоремы умножения – являются формула полной вероятности и формула Байеса. Пусть событие А может наступить при условии появления хотя бы одного из несовместных событий Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий
Формула полной вероятности
При этом события Пусть в условиях рассуждения, относящегося к формуле полной вероятности, произведено одно испытание, в результате которого произошло событие А. Спрашивается, как изменились (в связи с тем, что событие А уже произошло) вероятности гипотез, т.е. величины Найдем сначала условную вероятность По теореме умножения вероятностей имеем Отсюда где P(A) находится по формуле полной вероятности. Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т.е. условная вероятность любой гипотезы может быть вычислена по формуле
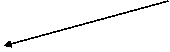
Формула Байеса Значение формулы Байеса состоит в том, что при появлении события А т.е. по мере поступления данных, получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы, основываясь на переходе от их исходных (априорных) вероятностей к пересмотренным (апостериорным) вероятностям гипотез.
Такой подход называется байесовским, дает возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т.п. Теоретические вопросы 1. События совместные и несовместные, зависимые и независимые. Условная вероятность события. 2. Теоремы сложения для совместных и несовместных событий. 3. Теоремы умножения для зависимых и независимых событий. 4. Формула полной вероятности. 5. Формула Байеса. 6. Назовите значение формулы Байеса. ЗАНЯТИЕ 3. |
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 332. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||

 События
События
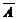 .
.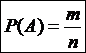 (1)
(1)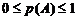 .
. (2)
(2)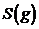 – площадь области g;
– площадь области g; 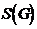 – площадь области G.
– площадь области G.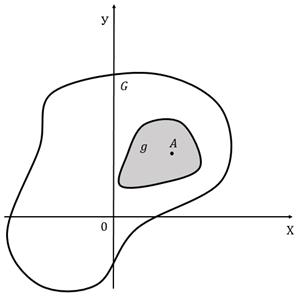 Обозначая меру (длину, площадь, объем) области через mes, приходим к следующему определению.
Обозначая меру (длину, площадь, объем) области через mes, приходим к следующему определению.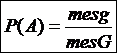 (3)
(3)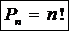 , (4)
, (4)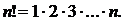
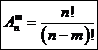 . (5)
. (5)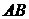 ,
,  ,
, 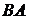 ,
, 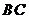 ,
, 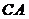 ,
, 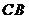 .
.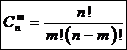 . (6)
. (6)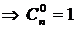
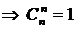
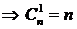
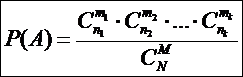 , (7)
, (7) .
.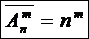 . (8)
. (8)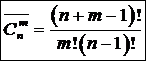 . (9)
. (9)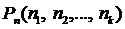 и вычисляется по формуле
и вычисляется по формуле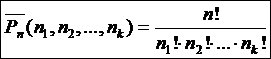 . (10)
. (10)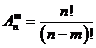
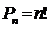
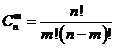
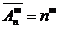
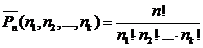
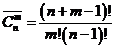
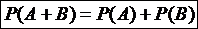 . (11)
. (11) . (12)
. (12)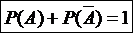 или
или 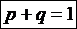 . (13)
. (13)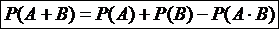 . (14)
. (14)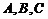 имеем:
имеем: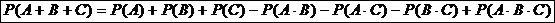 . (15)
. (15) , а затем воспользоваться равенством
, а затем воспользоваться равенством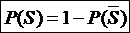 . (16)
. (16) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.
события В называется вероятность события В, найденная в предположении, что событие А уже наступило.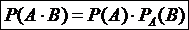 . (17)
. (17)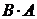 , получим:
, получим: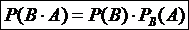 , (18)
, (18)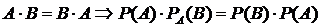 .
.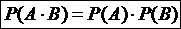 . (19)
. (19)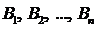 , которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности
, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности 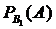 ,
, 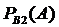 ,… события A. Как найти вероятность события А?
,… события A. Как найти вероятность события А?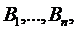 образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность событий А:
образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность событий А: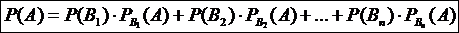 . (20)
. (20)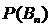 – вероятностями гипотез. Следствием теоремы умножения и формулы полной вероятности является формула Байеса. (Томас Байес (1702-1761) – английский математик).
– вероятностями гипотез. Следствием теоремы умножения и формулы полной вероятности является формула Байеса. (Томас Байес (1702-1761) – английский математик).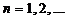 ?
?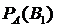 .
. .
.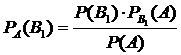 ,
,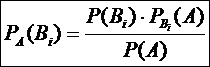 . (21)
. (21)