
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ.ФОРМУЛА БЕРНУЛЛИ. НАИВЕРОЯТНЕЙШЕЕ ЧИСЛО НАСТУПЛЕНИЙ СОБЫТИЯ Сведения из теории На практике часто приходится сталкиваться с задачами, которые можно представить в виде многократно повторяющихся испытаний при данном комплексе условий, в которых представляет интерес вероятность числа m наступлений некоторого события A в n испытаниях. Если вероятность наступления события A в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно событияA. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события A в каждом испытании одна и та же. Описанная последовательность независимых испытаний получила название схемы Бернулли. Теорема.Если вероятность p наступления события A в каждом испытание постоянна, то вероятность где Задача 3.1. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности возможности числа появления бракованных деталей среди 5 отобранных. Решение: Вероятность изготовления бракованной детали равна 0,2. Искомые вероятности находим по формуле Бернулли.
Полученные вероятности изобразим графически точками с координатами
Рис. 4 В частности, следует, что вероятность того, что в n испытаниях, удовлетворяющих схеме Бернулли, событие A наступит:  а) хотя бы один раз – равна б) менее k раз – равна в) более k раз – равна г) не менее k раз – равна д) не более k раз – равна Число
Теоретические вопросы 1. При каких условиях используют формулу Бернулли? 2. Повторные испытания: формула Бернулли. 3. По какой формуле вычисляют вероятность появления события А хотя бы один раз в n независимых испытаниях? 4. По какой формуле вычисляют вероятность появления события А более k раз в n независимых испытаниях? 5. По какой формуле вычисляют вероятность появления события А менее k раз в n независимых испытаниях? 6. По какой формуле вычисляют вероятность появления события А не менее k раз в n независимых испытаниях? 7. По какой формуле вычисляют вероятность появления события А неболее k раз в n независимых испытаниях? ЗАНЯТИЕ 4. ТЕОРЕМА ПУАССОНА. ЛОКАЛЬНАЯ ТЕОРЕМА МУАВРА - ЛАПЛАСА. ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА - ЛАПЛАСА Сведения из теории Если число испытаний n достаточно велико, то непосредственное вычисление по формуле Бернулли технически сложно, тем более если учесть, что сами p и q – числа дробные. Поэтому существуют более простые приближенные формулы для вычисления Теорема Пуассона. Если вероятность p наступления события A в каждом испытании стремится к нулю
Доказательство: По формуле Бернулли
Так как
Если вероятность p – постоянна и мала, число испытаний n – велико и число
Замечание 4.1Для вычисления факториалов больших чисел, используют формулу Стирлинга
Локальная теорема Муавра-Лапласа.Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность
где
Чем больше n, тем точнее приближенная формула (28). Приближенные значения вероятности Свойства функции Гаусса 1. Функция 2. Функция Нужно учитывать данные свойства при применении таблицы значений функции Интегральная теорема Муавра-Лапласа.Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что m наступления события A в n независимых испытаниях заключено в пределах от a до b (включительно), при достаточно большом числе n приближенно равна где
Формула (29) называется интегральной формулой Муавра-Лапласа. Чем больше n, тем точнее эта формула. Замечание 4.2При выполнении условия Замечание 4.3Функция Свойства функцииЛапласа 1. Функция 2. Функция Рассмотрим следствие интегральной теоремы Муавра-Лапласа. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе n независимых испытаний вероятность того, что: а) число m наступлений события A отличается от произведения
б) частность
в) частность
Теоретические вопросы 1. Какие формулы называются асимптотическими? 2. Приближенная формула Пуассона (доказательство). 3. Локальная теорема Муавра-Лапласа. 4. Интегральная теорема Муавра-Лапласа. 5. Функция Гаусса и ее свойства. 6. Функция Лапласа и ее свойства. 7. Следствие интегральной теоремы Муавра-Лапласа.
ЗАНЯТИЕ 5. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 329. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 того, что событие A наступит m раз в n независимых испытаниях, равна
того, что событие A наступит m раз в n независимых испытаниях, равна , (24)
, (24) .
.

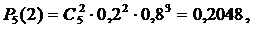



 Соединяя эти точки, получим многоугольник, или полигон распределения вероятностей (рис. 4).
Соединяя эти точки, получим многоугольник, или полигон распределения вероятностей (рис. 4).





 называется наивероятнейшим числом наступлений события A (или наиболее вероятным числом успехов) в схеме Бернулли, если
называется наивероятнейшим числом наступлений события A (или наиболее вероятным числом успехов) в схеме Бернулли, если  для всех m = 0,1,2,…,n. Если вероятности p и q отличны от нуля, то число
для всех m = 0,1,2,…,n. Если вероятности p и q отличны от нуля, то число  определяется из двойного неравенства
определяется из двойного неравенства . (25)
. (25)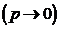 при неограниченном увеличении числа n испытаний
при неограниченном увеличении числа n испытаний  , причем произведение
, причем произведение 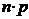 стремится к постоянному числу
стремится к постоянному числу 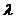
 , то вероятность
, то вероятность  . (26)
. (26) или, учитывая, что
или, учитывая, что 
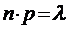 , т.е. при достаточно больших n,
, т.е. при достаточно больших n,  и
и

 и
и , то
, то 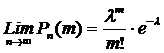 .
.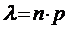 – незначительно (будем полагать, что
– незначительно (будем полагать, что  ), то из предельного равенства вытекает приближенная формула Пуассона
), то из предельного равенства вытекает приближенная формула Пуассона . (27)
. (27) .
. , (28)
, (28) – функция Гаусса,
– функция Гаусса, 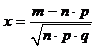 .
. порядка двух и более десятков, т.е. при условии
порядка двух и более десятков, т.е. при условии 
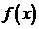 является четной, т.е.
является четной, т.е.  .
.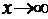 ,
,  .
. , (29)
, (29) – функция Лапласа (или интеграл вероятностей),
– функция Лапласа (или интеграл вероятностей), ,
, 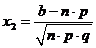 .
. формула (29) дает удовлетворительную погрешность вычисления вероятностей.
формула (29) дает удовлетворительную погрешность вычисления вероятностей. табулирована.
табулирована. .
. ,
,  (практически можно считать, что уже при
(практически можно считать, что уже при 
 ).
).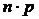 не более чем на величину
не более чем на величину  (по абсолютной величине), т.е.
(по абсолютной величине), т.е.
 . (30)
. (30) события A заключена в пределах от
события A заключена в пределах от  до
до 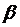 , т.е.
, т.е. , (31)
, (31)
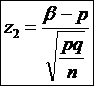 . (32)
. (32)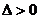 (по абсолютной величине), т.е.
(по абсолютной величине), т.е. . (33)
. (33)