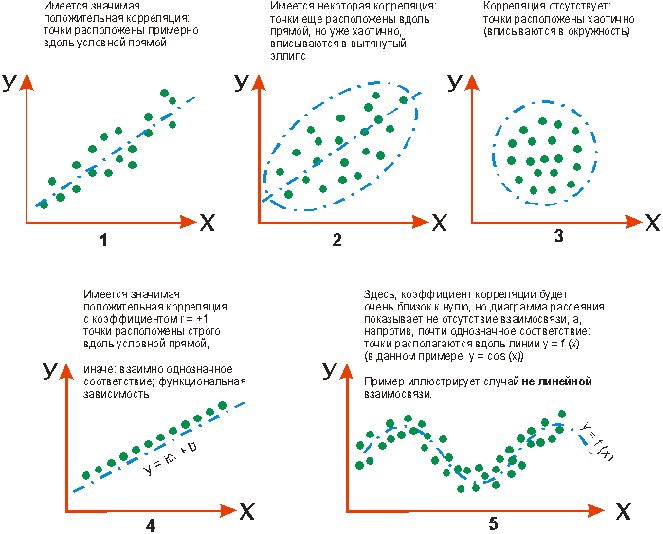
Интерпретация коэффициента корреляции.

1.Следует, прежде всего, помнить, что корреляция не является показателем зависимости одного фактора от другого, а лишь устанавливает их совместную вариативность. (Это относится, как к линейной, так и к ранговой корреляции). То обстоятельство, что два признака изменяются согласованно, может зависеть и от влияния третьей причины на оба сопоставляемых признака.

2. В общем случае коэффициент корреляции изменяется в пределах -1 <r< 1. Однако оценка высокого значения коэффициента корреляции как «сильной связи» справедлива только в случае нормального распределения признаков Х и У, то есть график их частот появления – симметричная колоколообразная кривая. В случае же наличияу этих признаков разнонаправленной асимметрии максимальный коэффициент корреляции бывает равен 0,6 – 0,7. Тогда встает вопрос: что означает получение в эксперименте такого коэффициента корреляции – сильную связь при наличии асимметрии или умеренную, даже слабую, - при нормальном распределении? Для более корректной содержательной интерпретации коэффициента корреляции необходимо строить каждый раз диаграммы рассеяния. Эти диаграммы, как в примере с тиграми, показывают характер узора, образованного точками-значениями переменных, см следующий рисунок:

3. Ошибка при интерпретации (даже еще при подсчете) коэффициента корреляции может быть допущена и в том случае, когда в выборке присутствуют аномальные значения (очевидно большие или очевидно низкие). Они могут возникать, во-первых, из-за неоднородности исследуемых элементов выборки. Во-вторых, - из-за ошибок. Например, снятые показания какого-либо прибора для удобства делились на три, но одно из наблюдений забыли пересчитать. В результате появится ряд, подобный этому:

0 4 2 6 6 2 9 8 25 3

8 9 1 0 5 2 4 6 35 1

Одной такой ошибки оказывается достаточно для того, чтобы коэффициент корреляции очень существенно увеличился.

4. Ложная корреляция может также возникать при неслучайном отборе наблюдений для подсчета. Этот пункт некоторым образом противоположен предыдущему (первой части). Если там утверждалось, что аномальные значения желательно исключать из рассмотрения, то этот пункт предлагает делать это с осторожностью, чтобы своим умышленным влиянием не исказить подлинное положение вещей.