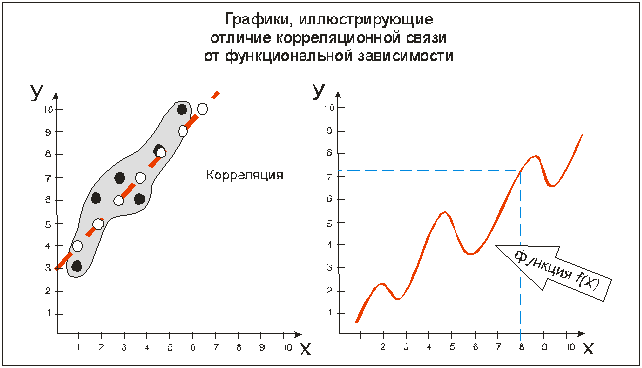
Линейная и ранговая корреляция.

Корреляционный анализ.

Корреляция – мера согласованности изменения случайных величин.

Корреляционная связьотражает тот факт, что изменения одной случайной величины находятся в некотором соответствии с изменениями другого. Корреляционная связь носит характер вероятностной.Важно отличать такую зависимость (даже если мы рискуем пользоваться этим термином) от функциональной зависимости. Функциональная зависимость предполагает взаимно однозначное соответствие аргумента х и функции f(х), вероятностная же зависимость допускает некий условный диапазон, в который предположительно (с такой-то долей вероятности) попадает значение случайной величины  у_i при значении х_i признака х.

Применение термина «корреляционная зависимость» уместно в тех случаях, когда мы сами контролируем воздействие одного признака на другой или так организуем эксперимент, что имеем возможность точно определить интенсивность не зависящих от нас воздействий (независимые переменные). Признаки, которые мы измеряем, и которые, по нашему предположению, могут меняться под заданным воздействием, называются зависимыми переменными. Иными словами, при принятом нами постоянстве одних переменных (независимых), фиксировано изменив их, мы предполагаем некоторое (неизвестное заранее) изменение исследуемых переменных (зависимых). Это деление, как уже было сказано, условно, так как неизвестно доподлинно, какой именно из признаков влияет на другой.

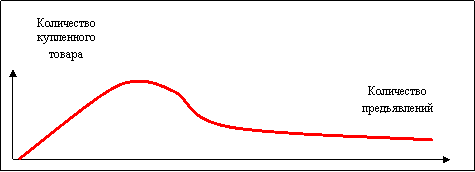
Корреляционные связи различаются по следующим характеристикам:

· по форме – зависимость может быть линейной и нелинейной(Пример1: покупаемость товара в зависимости от количества предъявлений его рекламы.)

· по направлению – усилению одного признака соответствует усиление другого припрямом направлении корреляции и ослабление - при обратном. (Важно: есть опасность ошибочного понимания того, что направление корреляции якобы указывает на то, какой признак на какой влияет. Направление указывает только на уменьшение-увеличение одного при изменении другого, но не более!)

· по силе – сила связи не зависит от направления и определяется абсолютной величиной коэффициента корреляцииr. При r = 1 наблюдается жесткая положительная связь, то есть при увеличении признака а обязательно увеличится признак b; при значении r =-1– гарантированно уменьшится; при значении r = 0– изменение а гарантированно никоим образом не повлечет за собой изменения b.

Классификация корреляционных связей по степени силы:

А) общая

Б) частная

Первая из классификаций ориентирована только на величину коэффициента корреляции, а вторая определяет, какого уровня значимости достигает данная величина коэффициента корреляции при данном объеме выборки. Чем больше объем выборки, тем меньшей величины коэффициента корреляции оказывается достаточно для того, чтобы корреляция была признана достоверной. В результате, при малом объеме выборки и сильная корреляция может оказаться недостоверной. (Это объясняется большой возможностью обнаружения случайных связей, поскольку число всех сочетаний в малых выборках также мало.) В то же время, при больших объемах выборки даже слабая корреляция между какими либо признаками может оказаться достоверной.

Линейная и ранговая корреляция.

Метод линейной корреляции (корреляции Пирсона) применяется для определения меры соответствия двух признаков, выраженных количественно, иными словами, - для численных величин. Это параметрический метод, который (как и прочие параметрические) требует соответствия распределения данного исследуемого признака закону нормального распределения. В отличие от этого метода, метод ранговой корреляции (корреляция Спирмена) применим к любым количественно измеренным или ранжированным данным. Этот метод способен, в отличие от других, измерять согласованность изменения разных признаков у одного испытуемого или выявлять совпадения индивидуальных ранговых показателей у двух испытуемых; или у испытуемого и усредненный показатель некой группы; или какие-либо показатели в сравнении двух групп.

Линейная корреляция.

Предположим, что мы располагаем выборкой данных о какой-то группе объектов. Пусть эти объекты обладают общими родовыми особенностями (примерно одинаковы). Пусть, к тому же, у каждого из объектов можно количественно измерить, как минимум, два каких-либо параметра. При этих обстоятельствах открывается возможность для подсчета линейной корреляции между двумя (или более) признаками, присущими этим объектам.

Требования и ограничения.

Необходимо иметь в виду, что сопоставляемые характеристики должны быть, во-первых, внутренне присущи объектам и, во-вторых, быть количественно-измеряемыми. Ввиду того, что расчет линейной корреляции проводится с использованием средних значений и дисперсий, следует также помнить, что эта процедура относится к разряду параметрических методов и, соответственно, требует нормальности распределения признака. Подробней об этом будет сказано ниже. Также следует помнить, что никакая корреляция вообще не устанавливает зависимости одного обстоятельства от другого, а лишь является мерой совместной вариации двух величин. И, наконец, линейная корреляция потому и называется линейной, что способна дать ответ о взаимосвязи изменений того и иного свойства объекта только тогда, когда возрастание-убывание значения признака происходит по линейному закону (график – прямая линия).