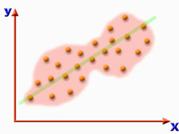
Графическое представление линейной корреляции.

Если теперь перейти к элементам выборки, то можно сказать, что точки, соответствующие этим элементам выстраиваются вдоль некоей воображаемой лини или вписываются в некую криволинейную фигуру. Отсюда следует, что чем меньше площадь этой фигуры, тем в большей согласованности находятся между собой сопоставляемые признаки, то есть больше коэффициент их корреляции. Уже на второй части рисунка можно построить такую воображаемую линию. Будем далее называть такой рисунок диаграммой рассеяния.

Итак, каждый элемент выборки обладает двумя свойствами (сопоставляемыми признаками), и может быть описан посредством задания двух его координат – Х и У.При этом всегда (это имеет смысл, если распределение близко к нормальному) можно подсчитать среднее значение для всех Х и для всех У. Таким образом, каждую точку на диаграмме можно полностью описать, указав величину ее отклонения от средних Х и У.

Если теперь суммировать произведения отклонений по всем элементам выборки, то получим величину:

 

n

Σ(X_i – X_ср) (У_i – У_ср)

i=1

Эта сумма будет велика и положительна, когда Х и У сильно связаны прямой взаимосвязью, и велика и отрицательна, в случае обратной взаимосвязи. Если же систематической связи не имеется (большим значениям Х одинаково часто сопутствуют и большие и малые значения У), результат суммирования будет близким к нулю.

Сама по себе эта сумма не пригодна в качестве меры взаимосвязи, поскольку учитывает количество элементов выборки (зависит от числа пар значений). Чтобы иметь возможность сопоставлять между собой «состояние дел» в выборках разных объемов, необходимо, чтобы показатель взаимосвязи не зависел от объема:

 

n

Σ(X_i – X_ср) (У_i – У_ср) = S_xy

i=1

--------------------------------------    

n – 1

Полученная величина S_xy называется ковариацией.

В качестве меры взаимосвязи надо избрать такую, которая не зависела бы ни от измерительных единиц, ни от средних, ни от дисперсий.

r_xy = S_xy /S_xS_y,     гдеS_xS_y– произведения стандартных отклонений.

Полученная величина называется коэффициентом корреляции.

Некоторые аспекты подсчета коэффициента корреляции

Ниже (без доказательства) будут приведены некоторые положения по подсчету коэффициента линейной корреляции.

1. В случае линейной функциональной зависимости между Х и У коэффициент корреляции между ними равен единице по абсолютной величине.

2. Коэффициент корреляции между Х и У не меняется при линейных преобразованиях этих переменных по типу с = кх + в. Это означает, что экспериментальные данные для удобства можно перемножать или складывать с константами. Важно только, чтобы все данные выборки были подвергнуты одинаковым преобразованиям.

3. Если исследовательская задача требует нахождения дисперсии суммы или разности двух переменных, между которыми известен коэффициент корреляции, то положительная корреляция способствует увеличению дисперсии такой суммы, а отрицательная – уменьшению.

4. Если при измерениях допущены ошибки (погрешности), то это обстоятельство уменьшает коэффициент корреляции между Х и У, по сравнению с тем, какой был бы получен при возможности использовать истинные значения измерений. Увеличение объема выборки не исправляет такого положения (если, разумеется, продолжать измерять что-либо прежними средствами). Например, при измерении набора каких-либо одинаковых деталей, произведенных портновским клеенчатым метром, мы получим каждый раз большие отклонения в ту или иную сторону, чем, если бы мерили рулеткой, штангенциркулем. Десять, сто, тысяча замеров не изменят положения вещей, поскольку метр растягивается, недостаточно точно градуирован, и т.п., и это будет одинаково справедливо для любого порядкового номера измерения. Ошибка, таким образом, не нейтрализуется со временем.

5. Если в выборку объектов, для которых установлен коэффициент корреляции между признаками Х и У поместить такие, для которых корреляция по Х и У отсутствует, итоговый коэффициент корреляции уменьшится по абсолютной величине.