
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Процедура синтеза дискретного корректирующего устройства ⇐ ПредыдущаяСтр 3 из 3
Рассмотрим задачу синтеза дискретного корректирующего устройства частотным методом, при котором в замкнутой системе при входном сигнале
Статический расчет
Сначала найдем условие на выбор коэффициента
где Полагая, что замкнутая система будет устойчивой, воспользуемся теоремой о конечном значении оригинала для определения установившейся ошибки [1]:
Для командного входного сигнала При значении Из выражения (26) с учетом равенства 
Динамический расчет
Найдем передаточную функцию
При этом желаемая передаточная функция разомкнутой системы имеет вид Следуя методике синтеза коррекции на основе ЛФЧХ, по передаточной функции
Тем самым в отличие критерия Найквиста непрерывных систем, для которых необходимо строить АФЧХ разомкнутой системы при изменении
Полагая здесь где При подстановке (28) в выражение Процедура синтеза последовательной коррекции состоит из следующих шагов. 1. С помощью обозначения
где символы "+" и "–" обозначают полиномы, корни которых имеют запасы устойчивости и не имеют запасов устойчивости соответственно. Формируется структура желаемой передаточной функции
Таким образом, желаемая передаточная должна содержать полиномы 2. По передаточной функции 3. С учетом свободы выбора полиномов 4. Определяется передаточная функция последовательной дискретной коррекции по ее логарифмической характеристике
или с помощью выражения
Выражение передаточной функции дикретной коррекции 5. По найденной передаточной функции дискретной коррекции Рассмотрим процедуру синтеза дискретной коррекции для ОУ (21) при следующих исходных данных: По формуле (26) найдем требуемый коэффициент усиления разомкнутой системы Синтез дискретной коррекции проведем с помощью программы составленной в Script-файле, который можно скопировать вместе с вспомогательным S-файлом с именем 'DiskrKor' из приложения к лабораторной работе:
kpas=100;Ty=0.01;Tdv=0.1; T0=0.05;% исходные данные % Передаточная функция непрерывной разомкнутой системы W0=tf([kpas],[1 0])*tf([1],[Tdv 1])*tf([1],[Ty 1]); % Дискретная передаточная функция нескорректированной % разомкнутой системы Wpasd=c2d(W0,T0); % ЛАХ и ЛФХ нескорректированной дискретной системы в псевдочастоте [nWpasd,dWpasd]=tfdata(Wpasd,'v'); NWpasd=poly2sym(nWpasd,'z'); DWpasd=poly2sym(dWpasd,'z'); s=sym('s'); z=(1+s*T0/2)/(1-s*T0/2); Ns=compose(NWpasd,z); Ds=compose(DWpasd,z); Ws=Ns/Ds; Ws=simple((Ws)); [nWs,dWs]=numden(Ws); nWs=sym2poly(expand(nWs));dWs=sym2poly(expand(dWs)); Wpass=tf(nWs,dWs); disp('Передаточная функция разомкнутой системы от оператора s'); zpk(Wpass) figure(1); margin(Wpass); grid; % Асимптотическая ЛАХ нескорректированной системы в псевдочастоте omega=[0.1 9.797 39.36 40 44.36 195.1 1000]; L1=20*log10(kpas/omega(1));L2=20*log10(kpas/omega(2)); L3=L2-40*log10(omega(3)/omega(2)); L4=L3-60*log10(omega(4)/omega(3)); L5=L4-40*log10(omega(5)/omega(4)); L6=L5-20*log10(omega(6)/omega(5));L7=L6; L=[L1 L2 L3 L4 L5 L6 L7]; figure(2); semilogx(omega,L); % Асимптотическая ЛАХ желаемой разомкнутой системы в псевдочастоте omega=[0.1 0.2 2 195.1 1000]; L1=20*log10(kpas/omega(1));L2=20*log10(kpas/omega(2)); L3=L2-40*log10(omega(3)/omega(2)); L4=L3-20*log10(omega(4)/omega(3)); L5=L4; L=[L1 L2 L3 L4 L5]; hold on; semilogx(omega,L,'r');grid on % красный цвет disp('Желаемая передаточная функция разомкнутой системы от s'); Wgs=kpas*tf([1/195.1 -1],[1 0])*tf([1/2 1],[1/0.2 1])*… tf([1/40 -1],[1/40 1]); zpk(Wgs) % Точные ЛАХ и ЛФХ, запасы устойчивости желаемой системы % в псевдочастоте figure(3);margin(Wgs);grid; % Последовательная коррекция в псевдочастоте Wks=Wgs/Wpass; Wks=minreal(Wks,1e-2);% постоянные времени с точность 0.01 % Обратный переход от псевдочастоты к z-изображению [nWks,dWks]=tfdata(Wks,'v'); NWks=poly2sym(nWks,'s'); DWks=poly2sym(dWks,'s'); z=sym('z'); s=2/T0*(z-1)/(z+1); Ns=compose(NWks,s); Ds=compose(DWks,s); Ws=Ns/Ds; Ws=simple((Ws)); [nWs,dWs]=numden(Ws); nWs=sym2poly(expand(nWs));dWs=sym2poly(expand(dWs)); disp('Дискретная коррекция в z-изображении') Wkd=minreal(tf(nWs,dWs,T0),1e-2);zpk(Wkd) % Построение переходной характеристики с помощью S- модели sim('DiskrKor');figure(4);hold on; simplot(y) В результате выполнения программы определяется передаточная функция Zero/pole/gain: 0.11169 (s-195.1) (s-40) (s+44.36) ---------------------------------- s (s+39.46) (s+9.797)
Для передаточной функции
Рис. 7
По передаточной функции
Рис. 8
На печать также выводится передаточная функция Zero/pole/gain: 0.051256 (s-195.1) (s-40) (s+2) ------------------------------- s (s+40) (s+0.2)
по которой строятся точные ЛАХ
Рис. 9
Для проверки выполнения заданных показателей качества с помощью S-файла с именем 'DiskrKor', вызываемого из программы, строится переходная характеристика замкнутой системы (рис. 10), из которой определяются На печать также выводится упрощенная передаточная функция Zero/pole/gain: 0.2811 (z-0.9048) (z-0.6065) ---------------------------- (z-0.99) (z+0.05173)
у которой учитываются нули и полюса по модулю с точностью Полученная передаточная функция будет работать устойчиво, т.е. ошибки вычисления накапливаться не будут.
Рис. 10
Расчётная часть
1. Для исходных данных
Таблица 1
2. Построить переходную характеристику скорректированной замкнутой системы и определить показатели качества 3. Записать алгоритм управления ЦВМ в виде выражения (20).
Экспериментальная часть
1. В системе Simulink провести моделирование системы (рис. 1) с помощью модели представленной на рис. 11. Здесь приняты обозначения передаточных функций W0
Рис. 11
Построить переходной процесс по ошибке Контрольные вопросы
1. Для какой цели используется идеальный импульсный элемент? 2. От чего зависит динамика процессов между моментами квантования? 3. В чем отличие z-преобразования от преобразования Лапласа? 4. От чего зависит установившаяся ошибка в дискретных системах? 5. В чем отличие частотных характеристик непрерывных и дискретных систем? 6. Для какой цели вводится вспомогательная псевдочастота при построении логарифмических частотных характеристик? 7. Почему для построения желаемой передаточной функции дискретной системы необходимо проводить факторизацию дискретной передаточной функции разомкнутой системы? 8. Каким образом реализуется закон управления по найденной передаточной функции дискретной коррекции? 9. Чем ограничено снизу значение периода квантования по времени? 10. Каким образом можно учесть при расчете дискретной коррекции время преобразования сигналов и счета ЦВМ?
Список литературы
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – С.-Петербург: изд. «Профессия», 2003. 2. Шамриков Б.М. Основы теории цифровых систем управления. М.: Машиностроение, 1985. 3. Гаркушенко В.И., Земляков А.С., Файзутдинов Р.Н. Нелинейные и дискретные системы автоматического управления. Уч. пособие. Казань: КГТУ им. А.Н. Туполева, 2000. |
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 189. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 для дискретных моментов времени
для дискретных моментов времени  ,
,  выполняются прямые показатели качества:
выполняются прямые показатели качества:  ,
,  ,
,  , где
, где  ,
,  и
и  – заданные ошибка, время регулирования и перерегулирование.
– заданные ошибка, время регулирования и перерегулирование. , при котором в замкнутой системе выполняется условие
, при котором в замкнутой системе выполняется условие  :
: ,
,
 . С учетом выражения (23) получим
. С учетом выражения (23) получим . (24)
. (24) .
.
 . (26)
. (26) формула (26) совпадает с установившейся ошибкой для непрерывной следящей системы, рассмотренной в лабораторной работе № 8. Однако здесь установившаяся ошибка рассматривается только для дискретных моментов времени
формула (26) совпадает с установившейся ошибкой для непрерывной следящей системы, рассмотренной в лабораторной работе № 8. Однако здесь установившаяся ошибка рассматривается только для дискретных моментов времени 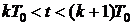 неизвестно. Возможны случаи существования «скрытых колебаний» в указанных интервалах времени, при которых
неизвестно. Возможны случаи существования «скрытых колебаний» в указанных интервалах времени, при которых  . Поэтому после проведения синтеза дискретного управления необходимо провести моделирование замкнутой системы по времени
. Поэтому после проведения синтеза дискретного управления необходимо провести моделирование замкнутой системы по времени  . Если при этом в установившемся режиме
. Если при этом в установившемся режиме  и заново провести синтез управления.
и заново провести синтез управления.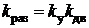 при
при  .
. по заданным показателям качества
по заданным показателям качества  разомкнутой нескорректированной системы с найденным коэффициентом
разомкнутой нескорректированной системы с найденным коэффициентом  :
: . (27)
. (27) . Тогда по известной передаточной функции
. Тогда по известной передаточной функции  определяется передаточная функция коррекции
определяется передаточная функция коррекции  .
. ,
,  можно построить ее ЛАХ
можно построить ее ЛАХ  и ЛФХ
и ЛФХ  при изменении
при изменении  . Поскольку
. Поскольку  является периодической функцией
является периодической функцией  с периодом, равным
с периодом, равным  , то при изменении
, то при изменении  многократно обегает окружность единичного радиуса против часовой стрелки (рис. 6). При этом функции
многократно обегает окружность единичного радиуса против часовой стрелки (рис. 6). При этом функции 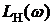 и
и  также являются периодическими функциями
также являются периодическими функциями  .
. Учитывая также, что функция
Учитывая также, что функция  симметрична относительно вещественной оси плоскости
симметрична относительно вещественной оси плоскости  : при значении
: при значении  для 1-го и 2-го квадрантов; при замене
для 1-го и 2-го квадрантов; при замене  на
на  для 3-го и 4-го квадрантов. При этом функция
для 3-го и 4-го квадрантов. При этом функция  соответственно будет иметь вид
соответственно будет иметь вид  и
и  , т.е. является симметричной относительно вещественной оси плоскости
, т.е. является симметричной относительно вещественной оси плоскости  .
. , получим
, получим , (28)
, (28) – вспомогательная псевдочастота, которая при изменении
– вспомогательная псевдочастота, которая при изменении  . При малых значениях
. При малых значениях  , т.к.
, т.к.  .
. уже в виде алгебраического выражения, для которого можно строить асимптотическую ЛАХ и проводить синтез коррекции ручным способом.
уже в виде алгебраического выражения, для которого можно строить асимптотическую ЛАХ и проводить синтез коррекции ручным способом. получим вспомогательную передаточную функцию
получим вспомогательную передаточную функцию  , для которой проводится факторизация:
, для которой проводится факторизация: ,
,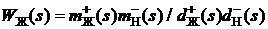 .
. ,
,  передаточной функции
передаточной функции  , также как для непрерывных систем.
, также как для непрерывных систем. строится асимптотическая желаемая ЛАХ
строится асимптотическая желаемая ЛАХ  по заданным показателям качества
по заданным показателям качества  ,
,  , которая изображается на графике ЛАХ нескорректированной системы
, которая изображается на графике ЛАХ нескорректированной системы  . При этом следует учитывать, что
. При этом следует учитывать, что  ,
, .
. определяется в результате обратного преобразования
определяется в результате обратного преобразования  .
. составляется алгоритм вычисления управляющего сигнала в виде выражения (20).
составляется алгоритм вычисления управляющего сигнала в виде выражения (20). ,
,  с,
с, 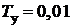 с;
с;  с;
с;  рад/с,
рад/с,  рад,
рад,  с,
с,  30%.
30%. .
. , которая выводится на печать:
, которая выводится на печать: (рис. 7), для которых найдены отрицательные запасы устойчивости по амплитуде
(рис. 7), для которых найдены отрицательные запасы устойчивости по амплитуде  дБ и фазе
дБ и фазе  град, что свидетельствует о неустойчивости замкнутой дискретной системы. При этом ЛАХ и ЛФХ
град, что свидетельствует о неустойчивости замкнутой дискретной системы. При этом ЛАХ и ЛФХ  в области низких частот.
в области низких частот.
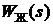 разомкнутой системы проводится с учетом
разомкнутой системы проводится с учетом  . При этом определяется желаемая частота среза
. При этом определяется желаемая частота среза  для
для  и соответственно
и соответственно  ,
,  . Построенные ЛАХ приведены на рис. 8.
. Построенные ЛАХ приведены на рис. 8.
 с указанием запасов устойчивости по амплитуде
с указанием запасов устойчивости по амплитуде  дБ и фазе
дБ и фазе  град (рис. 9).
град (рис. 9).
 с,
с,  %, удовлетворяющие заданным значениям.
%, удовлетворяющие заданным значениям.
 .
. ,
,  по модулю меньше единицы и, следовательно, алгоритм вычисления управляющего сигнала
по модулю меньше единицы и, следовательно, алгоритм вычисления управляющего сигнала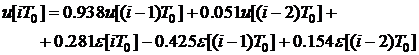

 с,
с,  .
. ,
, 

 для входного сигнала
для входного сигнала  , которую сравнить с заданной.
, которую сравнить с заданной.