Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Описание алгоритма управления ЦВМ
Перепишем выражение (5) в виде Тогда с учетом передаточной функции ЦВМ
Рассмотрим смысл выражения (15), полагая, что передаточная функция ЦВМ является алгебраическим выражением где Тогда выражение (15) можно записать в виде уравнения Перейдем к оригиналам в уравнении (17). Для этого сначала найдем оригинал выражения
то при нулевом начальном условии
Тем самым при нулевых начальных условиях
С учетом сказанного из уравнения (17) при нулевых начальных условиях оригиналов Отсюда в силу однозначности
Таким образом, алгоритм управления ЦВМ может быть реализован в виде вычислительной процедуры, задаваемой линейным разностным уравнением (19), где переменные
которое можно использовать для вычисления текущего значения управляющего сигнала для моментов времени  При учете временного запаздывания, связанного с временем преобразования сигналов в АЦП, ЦАП и временем счета в ЦВМ его можно отнести к непрерывной части системы. Для обеспечения в замкнутой системе требуемых показателей качества необходимо провести синтез алгоритма управления (20), т.е. определить его порядки
Математическое описание ОУ
В качестве обобщенного ОУ, также как и в лабораторной работе № 8, рассмотрим последовательно соединенные усилитель мощности, двигатель постоянного тока с независимым возбуждением и якорным управлением, редуктор и нагрузку. При этом выходной координатой
где С учетом инерционности усилителя мощности, его передаточная функция имеет вид где Соответственно полагаем Тогда передаточная функция ОУ будет иметь вид: где Согласно структурной схеме рис. 4
Учитывая, что
Здесь выражение
Найдем разложение множителя где Тогда помощью формул (10), (13), (14), (22) найдем выражение
с помощью которого можно записать выражение для передаточной функции: где после сокращения общих множителей числителя и знаменателя передаточной функции полиномы
Таким образом, получили уравнения замкнутой системы в z- изображениях:
которым соответствует структурная схема, представленная на рис. 5.
|
||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 156. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.  можно записать
можно записать .
.
 , (16)
, (16) ,
,  при
при  .
. . (17)
. (17) . Поскольку
. Поскольку ,
, оригиналом является решетчатая функция
оригиналом является решетчатая функция  . Аналогично для выражения
. Аналогично для выражения  при
при  можно записать
можно записать .
. справедлива общая формула
справедлива общая формула
 ,
,  получим
получим
 - преобразования следует уравнение для оригиналов:
- преобразования следует уравнение для оригиналов: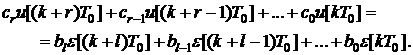 (19)
(19) ,
,  представляются в виде цифровых кодов. С помощью вспомогательной переменной
представляются в виде цифровых кодов. С помощью вспомогательной переменной  уравнение (19) можно переписать в виде
уравнение (19) можно переписать в виде (20)
(20) ,
,  Из уравнения (20) следует, что в алгоритм вычисления
Из уравнения (20) следует, что в алгоритм вычисления  входят операции сложения и умножения на постоянные коэффициенты, а также операции запоминания результатов вычислений и значений рассогласования на предшествующих шагах.
входят операции сложения и умножения на постоянные коэффициенты, а также операции запоминания результатов вычислений и значений рассогласования на предшествующих шагах. ,
,  и неизвестные коэффициенты
и неизвестные коэффициенты 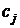 ,
,  ,
,  ,
,  .
. является измеряемый угол поворота вала редуктора, жестко связанного с инерционной нагрузкой. Для простоты будем полагать, что момент сопротивления, действующий на нагрузку, отсутствует. Пренебрегая индуктивностью якоря, нелинейностями характеристик двигателя, редуктора и усилителя мощности, передаточную функцию ОУ можно представить в виде
является измеряемый угол поворота вала редуктора, жестко связанного с инерционной нагрузкой. Для простоты будем полагать, что момент сопротивления, действующий на нагрузку, отсутствует. Пренебрегая индуктивностью якоря, нелинейностями характеристик двигателя, редуктора и усилителя мощности, передаточную функцию ОУ можно представить в виде ,
, – передаточная функция усилителя мощности;
– передаточная функция усилителя мощности;  – передаточные функции двигателя с учетом редуктора и инерционной нагрузки.
– передаточные функции двигателя с учетом редуктора и инерционной нагрузки. ,
,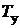 – постоянная времени,
– постоянная времени,  – коэффициент усиления, подлежащий определению.
– коэффициент усиления, подлежащий определению. .
. (21)
(21)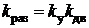 .
.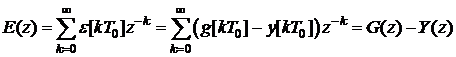 .
. , где
, где  , получим
, получим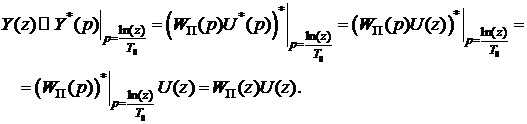
 можно записать в виде
можно записать в виде

 на сумму элементарных слагаемых:
на сумму элементарных слагаемых: , (22)
, (22) ,
,  ,
,  ,
,  ,
,  ,
, 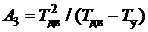 .
.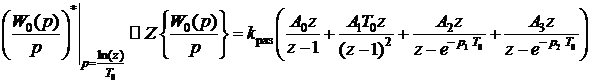 ,
,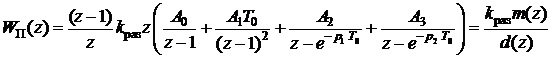 , (23)
, (23) и
и  имеют 3-й порядок:
имеют 3-й порядок: ,
,  .
.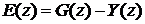 ,
, 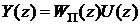 ,
,