Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Опр-ие: Ромб - это четырехугольник у к-ого все стороны равныСтр 1 из 3Следующая ⇒ Свойство: Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине. 8. Биссектриса - луч, выходящий из угла треугольника, делящий этот угол пополам 9. Свойство биссектрисы - Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам. 10.Свойство медианы треугольника - Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.
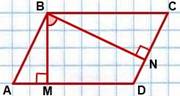
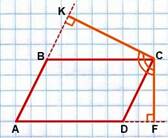
11. Признаки равенства треугольников: 1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. 3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. 12. Признаки подобия треугольников. (про отношение площадей и т.д. чет дичь) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.  Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны. 13. Определение и свойства параллелограмма: 1)Определение: Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны, то есть лежат на параллельных прямых. 2) Свойства: I. Противоположные стороны параллелограмма параллельны и равны II. Противоположные углы параллелограмма равны. III. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º. IV. Диагонали параллелограмма в точке пересечения делятся пополам. V. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон. AC²+BD²=2(AB²+AD²). VI. Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма. ∠MBN=∠A. VII. Угол между высотами параллелограмма, проведенными из вершины острого угла, равен тупому углу параллелограмма. ∠KCF=∠ABC. 14. Признаки параллелограмма: Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник — параллелограмм. Если две стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм. 15. Определение и свойства диагоналей прямоугольника: Опр-ие: Прямоугольник — это параллелограмм, у которого все углы прямые. Св-во диагоналей: Диагонали прямоугольника равны. 16. Определение и свойство диагоналей ромба: Опр-ие: Ромб - это четырехугольник у к-ого все стороны равны |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 330. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
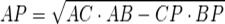 - формула нахождения биссектрисы
- формула нахождения биссектрисы