
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные цели и задачи прикладного корреляционно-регрессионного анализаРассмотрим некоторый экономический объект (процесс, явление, систему) и выделим только две переменные, характеризующие объект. Обозначим переменные буквами Y и X. Будем предполагать, что независимая (объясняющая) переменная X оказывает воздействие на значения переменной Y, которая, таким образом, является зависимой переменной, т.е. имеет место зависимость: Y=f(X). (2.1) Зависимость (2.1) можно рассматривать с целью установления самого факта наличия или отсутствия значимой связи между Y и X, можно преследовать цель прогнозирования неизвестных значений Y по известным значениям X, наконец возможно выявление причинно-следственных связей между X и Y. При изучении взаимосвязи между переменными Y и X следует, прежде всего, установить тип зависимости (природу анализируемых переменных Y и X). Возможны следующие ситуации: q Y и X являются неслучайными переменными, т.е. значения Y строго зависят только от соответствующих значений X и полностью ими определяются. В этом случае говорят о функциональной зависимости, когда Y является некоторой функцией от переменной X и верна модель (2.1). Пример: q Y является случайной переменной, а X – неслучайной. В этом случае считают, что между переменными имеет место регрессионная зависимость. То есть верна модель Y=f(X)+u, где u – величина случайной ошибки. q Y и X зависят от множества неконтролируемых факторов, так что являются случайными по своей сущности. В этом случае к проблемам построения конкретного вида зависимости между указанными переменными присоединяется проблема исследования тесноты связи между этими переменными. Речь в этом случае идет о корреляционно-регрессионной зависимости между Y и X.  Будем предполагать наличие второй из указанных ситуаций. Регрессионный анализ является инструментом решения следующих основных задач: 1. Для любых значений объясняющей переменной X построить наилучшие по некоторому критерию оценки для неизвестной функции f(X). 2. По заданным значениям объясняющей переменной X построить наилучший по некоторому критерию прогноз для неизвестного значения результирующей переменной Y(X). 3. Пусть известно, что искомая функция зависит от параметра q: f(X, q). Требуется построить наилучшую в определенном смысле оценку для неизвестного значения этого параметра. 4. Оценить удельный вес влияния переменной X на результирующий показатель Y. В следующих разделах параграфа рассмотрим процедуру решения этих задач. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 662. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
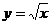 .
.