
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методологические вопросы построения эконометрических моделейВ любой эконометрической модели, в зависимости от конечных прикладных целей ее использования все участвующие в ней переменные подразделяются на: - экзогенные переменные, задаваемые как бы извне, автономно, в определенной степени управляемые (планируемые); - эндогенные переменные, значения которых формируются в процессе и внутри функционирования анализируемой социально-экономической системы под воздействием экзогенных переменных и во взаимодействии друг с другом, являются предметом объяснения в эконометрической модели; - предопределенные переменные выступают в роли факторов-аргументов или объясняющих переменных; - лаговые эндогенные переменные входят в уравнения анализируемой эконометрической системы, но измерены в прошлые моменты, а следовательно, являются уже известными, заданными. Эконометрическая модель служит для объяснения поведения эндогенных переменных в зависимости от значений экзогенных и лаговых эндогенных переменных. Весь процесс эконометрического моделирования можно разбить на шесть основных этапов. 1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли; 2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез; 3-й этап (параметризация) – собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными;  4-й этап (информационный) – сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей; 5-й этап (идентификация модели) – статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели. Непосредственно связан с проблемой идентифицируемости модели, то есть ответа на вопрос «Возможно ли в принципе однозначно восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответствии с решением, принятым на этапе параметризации?». После положительного ответа на этот вопрос необходимо решить проблему идентификации модели, то есть предложить и реализовать математически корректную процедуру оценивания неизвестных параметров модели по имеющимся исходным данным; 6-й этап (верификация модели) – сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных. В ходе верификации модели решаются вопросы о том: - насколько удачно удалось решить проблемы спецификации, идентифицируемости и идентификации, т.е. можно ли рассчитывать на то, что использование полученной модели в целях прогноза даст результаты, адекватные действительности; - какова точность (абсолютная, относительная) прогнозных и имитационных расчетов основанных на построенной модели; Получение ответов на эти вопросы с помощью тех или иных математико-статистических методов и составляет содержание верификации модели. Проблема спецификации модели решается на 1, 2, 3 этапах моделирования и включает в себя: - определение конечных целей моделирования (прогноз, имитация сценариев развития анализируемой системы, управление); - определение списка экзогенных и эндогенных переменных; - определение состава анализируемой системы уравнений и тождеств и соответственно списка предопределенных переменных; - формулировка исходных предпосылок и априорных ограничений относительно стохастической природы остатков (рассмотрение проблемы гомоскедастичности). Этапы 4, 5 и 6 сопровождаются процедурой калибровки модели, которая заключается в переборе большого числа вариантов, обусловленных наличием «нормативных» ограничений, определенных содержательным смыслом анализируемых связей и определенной нечеткостью (неполнотой) статистической информации. Калибровка модели - трудоемкая процедура, что связано с многократными «вычислительными прогонами» модели. Наиболее распространенными в эконометрическом моделировании являются следующие образующие четыре группы методы: - классическая линейная модель множественной регрессии (КЛММР) и классический метод наименьших квадратов (МНК); - обобщенная КЛММР и обобщенный МНК; - методы статистического анализа временных рядов; - методы анализа систем одновременных эконометрических уравнений. Применение этих методов делает возможным построение следующих типов эконометрических моделей: 1. Регрессионные модели с одним уравнением. В таких моделях зависимая (объясняемая) переменная
где
В зависимости от вида функции Например, можно исследовать уровень дохода семьи как функцию от ряда ее экономических и социально-демографических характеристик (наличие и количество работников в семье, наличие и количество детей и прочих иждивенцев, уровень образования и квалификации главы семьи и т.д.). 2. Модели временных рядов. К этому классу относятся модели: · тренда: где t – время,
x - случайная (стохастическая) компонента; · сезонности: где · тренда и сезонности: где Кроме того, существуют модели временных рядов, в которых присутствует циклическая компонента, формирующая изменения анализируемого признака, обусловленные действием долговременных циклов экономической, демографической или астрофизической природы (волны Кондратьева, циклы солнечной активности и т.д.). Модели временных рядов могут применяться для изучения и прогнозирования объема продаж туристических путевок, спроса на железнодорожные и авиабилеты, при краткосрочном прогнозировании процентных ставок и т.д. 3. Системы одновременных уравнений. Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых, кроме объясняющих переменных, может включать в себя объясняемые переменные из других уравнений системы. Системы одновременных уравнений требуют сложного математического аппарата и могут быть использованы для моделей национальной экономики. Ярким примером системы одновременных уравнений служит модель спроса и предложения. Пусть Составим систему уравнений "спрос – предложение":
Цена товара Pt и спрос на товар Для эконометрического моделирования используются данные следующих трех типов. 1. Предположим, что мы располагаем результатами регистрации значений переменных
Такой тип данных называется пространственной выборкой или данными поперечного среза (cross-section data). Такие данные не имеют временного параметра, и порядок их следования не существенен. Пример: финансовые показатели работы предприятий за истекший год. 2. Предположим, что данные регистрируются на одном и том же объекте, но в разные периоды времени. Тогда аналогом i будет номер периода времени, к которому привязаны соответствующие данные, а n будет общим числом периодов времени. Такие данные называются временнóй выборкой, или временными рядами данных (time series data), или данными продольного среза. Для таких данных существенен порядок следования значений переменных. Пример: финансовые показатели предприятия за последние несколько лет. 3. Наконец, предположим, что отслеживается каждый из n объектов в течение T периодов времени. То есть имеем последовательность матриц вида X, отнесенных к моментам времени 1,2,…,Т:
Такие данные называются панельными, или пространственно-временной выборкой (panel data). Данные сочетают в себе свойства как временных рядов, так и данных поперечного сечения. Как правило, значение T мало. Пример: показатели социально-экономического состояния домохозяйств за три года. Парная регрессия |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 666. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 представляется в виде функции
представляется в виде функции ,
, - независимые (объясняющие) переменные,
- независимые (объясняющие) переменные, - параметры.
- параметры. модели делятся на линейные и нелинейные.
модели делятся на линейные и нелинейные. ,
, - временной тренд заданного параметрического вида (например, линейный
- временной тренд заданного параметрического вида (например, линейный  ),
), ,
, - периодическая (сезонная) компонента,
- периодическая (сезонная) компонента, - случайная (стохастическая) компонента.
- случайная (стохастическая) компонента. (аддитивная) или
(аддитивная) или (мультипликативная)
(мультипликативная) - спрос на товар в момент времени t,
- спрос на товар в момент времени t,  - предложение товара в момент времени t,
- предложение товара в момент времени t,  - цена на товар в момент времени t, Yt – доход в момент t.
- цена на товар в момент времени t, Yt – доход в момент t. (предложение),
(предложение), (спрос),
(спрос), (равновесие).
(равновесие). определяются из уравнений модели, то есть являются эндогенными переменными. Объясняющими переменными в данной модели являются доход Yt и значение цены товара в предыдущий момент времени
определяются из уравнений модели, то есть являются эндогенными переменными. Объясняющими переменными в данной модели являются доход Yt и значение цены товара в предыдущий момент времени  .
. на n статистически обследованных объектах. Так что если i – номер обследованного объекта, то имеющиеся исходные статистические данные состоят из n строк вида
на n статистически обследованных объектах. Так что если i – номер обследованного объекта, то имеющиеся исходные статистические данные состоят из n строк вида  , где
, где  - значение j переменной, зарегистрированное на i обследованном объекте. То есть данные могут быть представлены в виде матрицы n´p:
- значение j переменной, зарегистрированное на i обследованном объекте. То есть данные могут быть представлены в виде матрицы n´p: .
.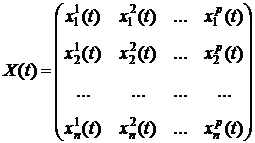 .
.